Задачи для самостоятельного решения. I. Для функции у найти . 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 13) ; 7) ; 8) ; 9) ; 10) ; 11) ; 12) ;
I. Для функции у найти 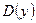 .
.
1) 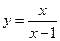 ; 2) ; 2) 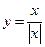 ; 3) ; 3) 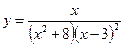 ; 4) ; 4) 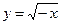 ; 5) ; 5) 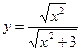 ; 6) ; 6) 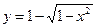 ; 13) ; 13) 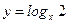 ; ; | 7) 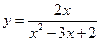 ; 8) ; 8) 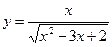 ; 9) ; 9) 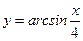 ; 10) ; 10) 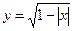 ; 11) ; 11) 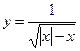 ; 12) ; 12) 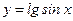 ; 14) ; 14) 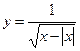 . . |
II. Для указанных ниже функций определить, будет ли функция чётной, нечетной, функцией общего вида.
1) 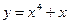 ; 2) ; 2) 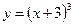 ; 3) ; 3) 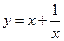 ; 4) ; 4) 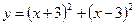 ; 5) ; 5) 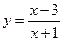 ; 6) ; 6) 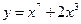 ; ; | 7) 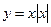 ; 8) ; 8) 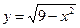 ; 9) ; 9) 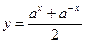 ; 10) ; 10) 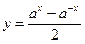 ; 11) ; 11) 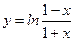 . . |
Ответы:
I. 1) 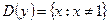 ; 2)
; 2) 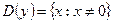 ;
;
3) 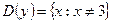 ; 4)
; 4) 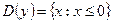 ;
;
5) 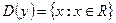 ; 6)
; 6) 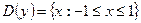 ;
;
7) 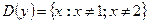 ; 8)
; 8) 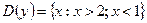 ;
;
9) 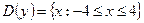 ; 10)
; 10) 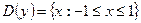 ;
;
11) 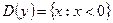 ;
;
12) 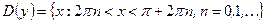 ;
;
13) 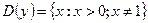 ; 14)
; 14) 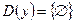 .
.
II. 1), 2), 5) – функция общего вида;
3), 6), 7), 10), 11) – функция нечетная;
4), 8), 9) – функция четная.
Занятие 2.
Полярная система координат. Построение графиков функций методом сдвига и растяжения вдоль осей координат.
Основные элементы полярной системы координат – полярная ось и полюс. По отношению к ним определяется положение точки на плоскости. Полярные координаты точки 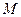 – это пара чисел
– это пара чисел 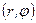 , где
, где 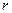 – расстояние от
– расстояние от 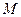 до полюса
до полюса 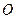 , а
, а 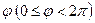 – это угол между полярной осью и
– это угол между полярной осью и 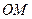 . (см. рис.1).
. (см. рис.1).

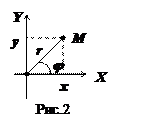
Пусть полярная система координат расположена так, что полюс совпадает с началом декартовой системы координат, а полярная ось – с осью ОХ. Пусть точка 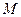 имеет декартовы координаты
имеет декартовы координаты 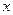 и
и 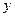 , т.е.
, т.е. 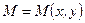 , а полярные –
, а полярные – 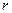 и
и 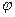 , т.е., с другой стороны,
, т.е., с другой стороны, 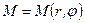 (см. рис.2).
(см. рис.2).
Тогда:
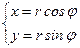 ;
; 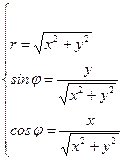
Примеры.
1)Даны декартовы координаты точки 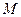 :
: 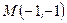 . Найти её полярные координаты, т.е.
. Найти её полярные координаты, т.е. 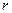 и
и 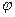 .
.
▲ Имеем: 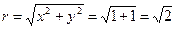 ,
, 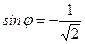 ,
,
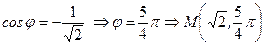 .
.
2)Даны полярные координаты точки 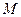 :
: 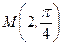 . Найти её декартовы координаты, т.е.
. Найти её декартовы координаты, т.е. 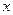 и
и 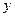 .
.
▲ Имеем: 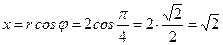 ,
,
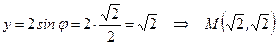 .
.
3)Задать кривые в полярных координатах (при помощи уравнения 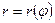 ).
).
а) 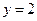 ; б)
; б) 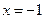 ; в)
; в) 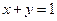 .
.
▲ Подставим в уравнение кривой вместо 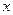 выражение
выражение 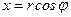 , а вместо
, а вместо 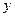 – выражение
– выражение 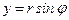 , и выразим
, и выразим 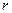 через
через 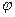 :
:
а) 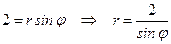 ;
;
б) 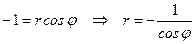 ;
;
в) 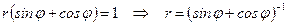 .
.
Геометрические преобразования графиков функций
Предположим, что построен график функции 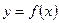 . Требуется построить на его основе график функции
. Требуется построить на его основе график функции 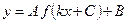 , где
, где 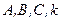 – константы. Далее в таблице приведен ряд правил построения таких графиков.
– константы. Далее в таблице приведен ряд правил построения таких графиков.
| Преобразование функции | Преобразование графика | |
| 1) | 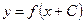 | График 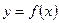 сдвигается вдоль оси сдвигается вдоль оси 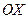 на на 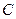 "единиц" вправо, если "единиц" вправо, если 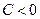 , и " , и " 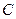 " единиц влево, если " единиц влево, если 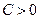 . . |
| 2) | 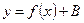 | График 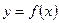 сдвигается вдоль оси сдвигается вдоль оси 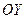 на " на " 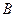 " единиц вверх, если " единиц вверх, если 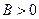 , и " , и " 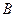 " единиц вниз, если " единиц вниз, если 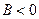 . . |
| 3) | 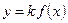 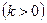 | При 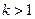 график график 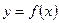 растягивается в растягивается в 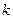 раз вдоль оси раз вдоль оси 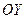 ; при ; при 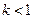 график график 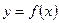 сжимается в сжимается в 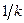 раз вдоль оси раз вдоль оси 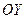 . . |
| 4) | 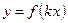 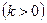 | При 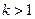 график график 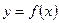 сжимается к оси сжимается к оси 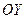 в в 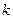 раз; при раз; при 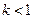 график график 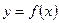 растягивается от оси растягивается от оси 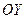 в в 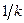 раз. раз. |
| 5) | 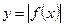 | Сохранить часть графика 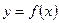 над осью над осью  , а то, что под , а то, что под  – отразить симметрично относительно – отразить симметрично относительно 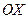 . . |
| 6) | 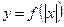 | Сохранить часть графика 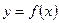 при при 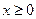 , и, кроме того, эту часть отразить симметрично относительно оси , и, кроме того, эту часть отразить симметрично относительно оси 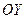 . . |
| 7) | 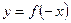 | График 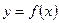 отразить симметрично относительно отразить симметрично относительно 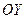 . . |
| 8) | 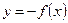 | График 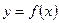 отразить симметрично относительно отразить симметрично относительно 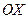 . . |
Замечания.
1)Применяя последовательно эти приемы, можно построить график функции вида 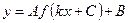 ;
;
2)Период функций 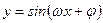 ,
, 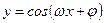 равен
равен 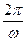 .
.
Примеры.
I. Случаи 1), 2).
а) Рассмотрим функцию 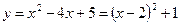 . График этой функции можно получить путем сдвига "стандартной" параболы
. График этой функции можно получить путем сдвига "стандартной" параболы 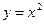 как единого целого на две единицы по оси
как единого целого на две единицы по оси 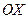 вправо и на одну единицу по оси
вправо и на одну единицу по оси 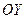 вверх (см. рис.3).
вверх (см. рис.3).
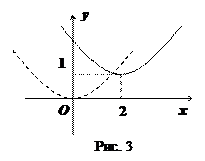
б) Рассмотрим функцию 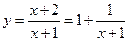 . График этой функции можно получить путем сдвига "стандартной" гиперболы
. График этой функции можно получить путем сдвига "стандартной" гиперболы 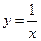 по оси
по оси  влево на одну единицу и по оси
влево на одну единицу и по оси  вверх на одну единицу (см. рис.4).
вверх на одну единицу (см. рис.4).
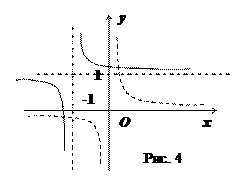
II. Случаи 3), 4).
а) Рассмотрим функцию 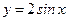 . График этой функции можно получить путем растяжения графика функции
. График этой функции можно получить путем растяжения графика функции 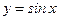 вдоль оси
вдоль оси  в 2 раза. При этом нули обеих функций одинаковы – это точки вида
в 2 раза. При этом нули обеих функций одинаковы – это точки вида 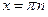 ,
, 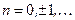 (см. рис.5).
(см. рис.5).
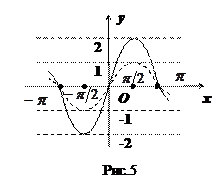
б) Рассмотрим функцию 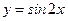 . График этой функции можно получить из графика
. График этой функции можно получить из графика 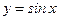 путем сжатия его в 2 раза к оси
путем сжатия его в 2 раза к оси 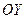 . Период функции
. Период функции 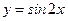 равен
равен 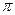 (см. рис.6).
(см. рис.6).
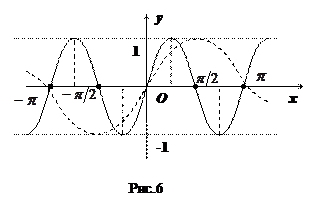 |
III. Случаи 5), 6).
Рассмотрим функции 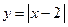 и
и 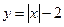 . Их графики можно получить из графика функции
. Их графики можно получить из графика функции 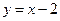 по правилам 5) или 6) (см. рис.7 и рис.8).
по правилам 5) или 6) (см. рис.7 и рис.8).
|

IV. Случаи 7), 8).
Рассмотрим функции 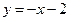 и
и 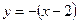 . Их графики можно получить из графика функции
. Их графики можно получить из графика функции 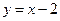 по правилам 7) и 8), соответственно (см. рис.9 и рис.10).
по правилам 7) и 8), соответственно (см. рис.9 и рис.10).
 |
