Несобственные интегралы
Вычислить несобственный интеграл 1 рода или установить его расходимость:
635. 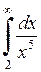 . . | 636. 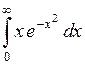 . . | 637. 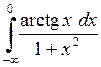 . . | 638. 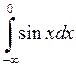 . . |
639. 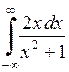 . . | 640. 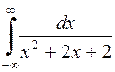 . . | 641. 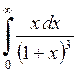 . . | 642. 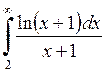 . . |
Вычислить несобственный интеграл 2 рода или установить его расходимость:
643. 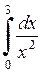 . . | 644. 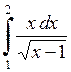 . . | 645. 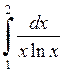 . . | 646. 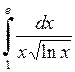 . . |
647. 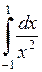 . . | 648. 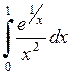 . . | 649. 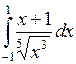 . . | 650. 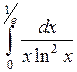 . . |
Ответы.635. 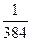 . 536.
. 536. 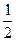 . 637.
. 637. 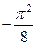 . 638. Расходится. 639. Расходится. 640.
. 638. Расходится. 639. Расходится. 640. 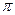 .
.
641. 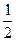 . 642. Расходится. 643. Расходится. 644.
. 642. Расходится. 643. Расходится. 644. 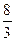 . 645. Расходится. 646.
. 645. Расходится. 646. 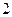 .
.
647.  , расходится. 648.
, расходится. 648. 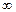 , расходится. 649.
, расходится. 649. 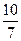 . 650.
. 650. 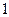 .
.
Двойной интеграл
651.-664. Расставить пределы интегрирования и вычислить двойные интегралы:
651. 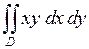 ,
, 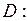
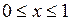 ,
, 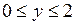 .
.
652. 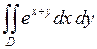 ,
, 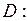
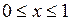 ,
, 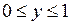 .
.
653. 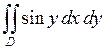 ,
, 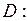
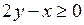 ,
, 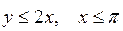 .
.
654. 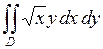 ,
, 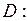
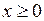 ,
, 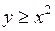 ,
, 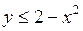 .
.
655. 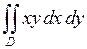 ,
, 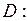
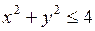 ,
, 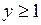 .
.
656. 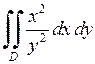 ,
, 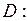
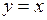 ,
, 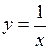 ,
, 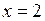 .
.
657. 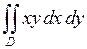 ,
, 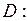
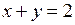 ,
, 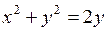 (выше прямой).
(выше прямой).
658. 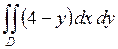 ,
, 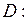
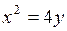 ,
, 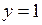 ,
, 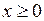 .
.
659. 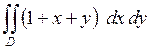 ,
, 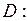
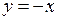 ,
, 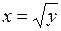 ,
, 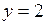 .
.
660. 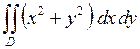 ,
, 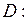
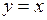 ,
, 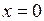 ,
, 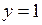 ,
, 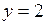 .
.
661. 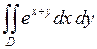 ,
, 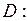
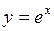 ,
, 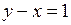 ,
, 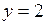 .
.
662. 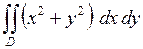 ,
, 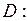
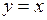 ,
, 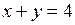 ,
, 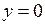 .
.
663. 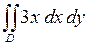 ,
, 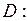
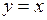 ,
, 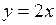 ,
, 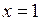 ,
, 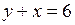 .
.
664. 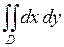 ,
, 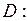
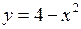 ,
, 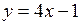 ,
, 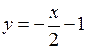 .
.
665.-670. Перейти к полярным координатам и вычислить интеграл:
665. 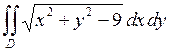 ,
, 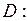
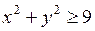 ,
, 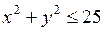 .
.
666. 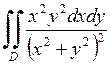 ,
, 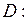
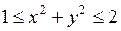 .
.
667. 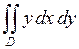 ,
, 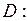
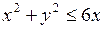 .
.
668. 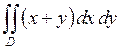 ,
, 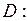
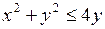 .
.
669. 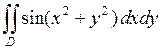 ,
, 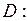
 ,
, 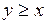 ,
, 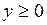 .
.
670. 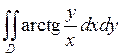 ,
, 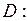
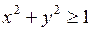 ,
, 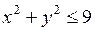 ,
, 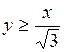 ,
, 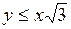 .
.
671. Найти площадь, ограниченную линиями 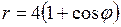 ,
, 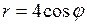 .
.
672. Найти площадь, ограниченную линиями 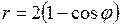 ,
, 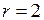 (вне кардиоиды).
(вне кардиоиды).
Ответы.651. 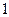 . 652.
. 652. 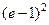 . 653. 2. 654.
. 653. 2. 654. 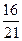 . 655. 0. 656.
. 655. 0. 656. 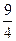 . 657.
. 657. 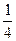 . 658.
. 658. 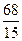 .
.
659. 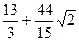 . 660.
. 660. 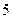 . 661.
. 661. 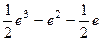 . 662.
. 662. 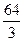 . 663.
. 663. 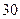 . 664. 9. 665.
. 664. 9. 665. 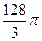 .
.
666. 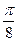 . 667. 0. 668.
. 667. 0. 668. 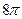 . 669.
. 669. 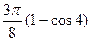 . 670.
. 670. 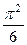 . 671.
. 671. 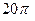 . 672.
. 672. 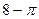 .
.
Тройной интеграл
673.-676. Вычислить тройные интегралы:
673. 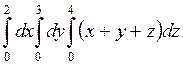 . 674. . 674. 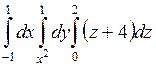 . . |
675. 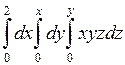 . 676. . 676. 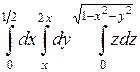 . . |
677.-682. Вычислить тройные интегралы по областям, ограниченным указанными поверхностями:
677. 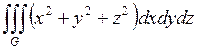 ; ; 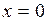 , , 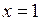 , , 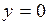 , , 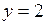 , , 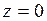 , , 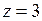 . . |
678. 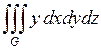 ; ; 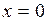 , , 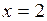 , , 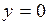 , , 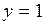 , , 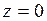 , , 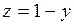 . . |
679. 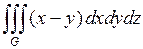 ; ; 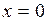 , , 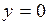 , , 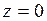 , , 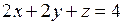 . . |
680. 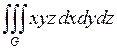 ; ; 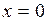 , , 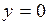 , , 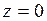 , , 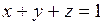 . . |
681. 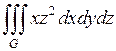 ; ; 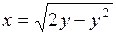 , , 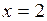 , , 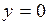 , , 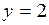 , , 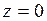 , , 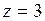 . . |
682. 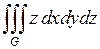 ; ; 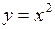 , , 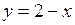 , , 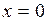 , , 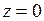 , , 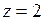 . . |
683.-686. Вычислить интегралы с помощью перехода к цилиндрическим координатам:
683. 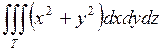 , , 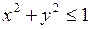 , , 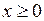 , , 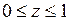 . . |
684. 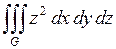 , , 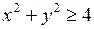 , , 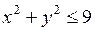 , , 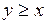 , , 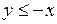 , , 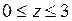 . . |
685. 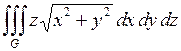 , , 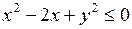 , , 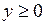 , , 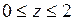 . . |
686. 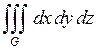 , , 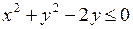 , , 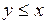 , , 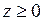 , , 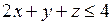 . . |
Ответы.673.108. 674. 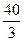 . 675.
. 675. 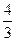 . 676.
. 676. 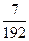 . 677. 28. 678.
. 677. 28. 678. 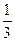 . 679. 0.
. 679. 0.
680. 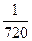 . 681.
. 681. 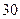 . 682.
. 682. 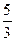 . 683.
. 683. 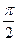 . 684.
. 684. 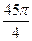 . 685.
. 685. 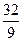 . 686.
. 686. 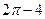 .
.
Дифференциальные уравнения первого порядка
687.-694. Найти общее решение дифференциального уравнения с разделяющимися переменными:
687. 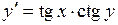 . . | 688. 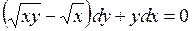 . . |
689. 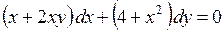 . . | 690. 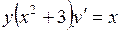 . . |
691. 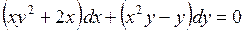 . . | 692. 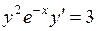 . . |
693. 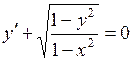 . . | 694. 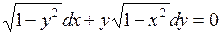 . . |
695.-696. Найти частное решение дифференциального уравнения при заданном условии:
695. 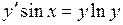 , , 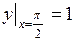 . . | 696. 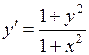 , , 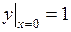 . . |
697.-702. Найти общее решение однородного уравнения:
697. 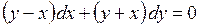 .698.
.698. 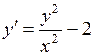 . 699.
. 699. 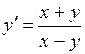 .
.
700. 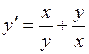 . 701.
. 701. 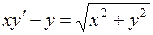 . 702.
. 702. 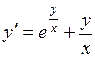 .
.
703.-704. Найти частное решение дифференциального уравнения при заданном условии:
703. 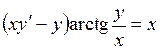 ,
, 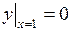 . 704.
. 704. 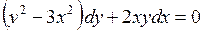 ,
, 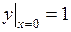 .
.
705.-710. Найти общее решение линейного дифференциального уравнения:
705. 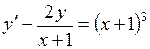 . 706.
. 706. 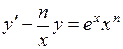 .
.
707. 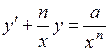 . 708.
. 708. 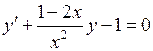 .
.
709. 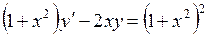 . 710.
. 710. 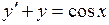 .
.
711.-712. Найти частное решение дифференциального уравнения при заданном условии:
711. 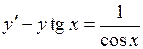 , , 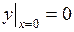 . . | 712. 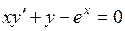 , , 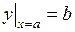 . . |
713.-716. Найти общее решение уравнения Бернулли:
713. 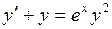 . 714.
. 714. 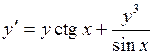 .
.
715. 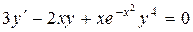 . 716.
. 716. 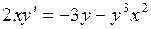 .
.
717.-722. Найти общее решение дифференциального уравнения в полных дифференциалах:
717. 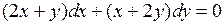 .
.
718. 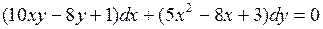 .
.
719. 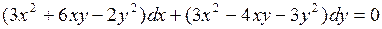 .
.
720. 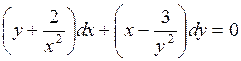 .
.
721. 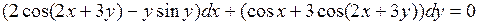 .
.
722. 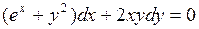 .
.
Ответы.687. 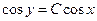 . 688.
. 688. 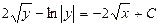 . 689.
. 689. 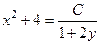 .
.
690. 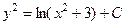 . 691.
. 691. 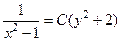 . 692.
. 692. 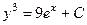 . 693.
. 693. 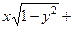
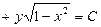 . 694.
. 694. 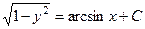 . 695.
. 695. 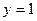 . 696.
. 696. 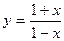 . 697.
. 697. 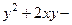
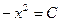 . 698.
. 698. 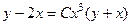 . 699.
. 699. 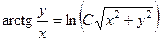 . 700.
. 700. 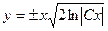 .
.
701. 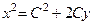 . 702.
. 702. 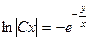 . 703.
. 703. 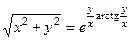 . 704.
. 704. 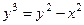 .
.
705. 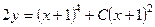 . 706.
. 706. 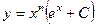 . 707.
. 707. 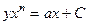 . 708.
. 708. 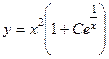 .
.
709. 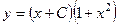 . 710.
. 710. 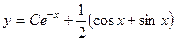 . 711.
. 711. 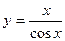 . 712.
. 712. 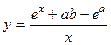 .
.
713. 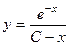 . 714.
. 714. 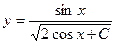 . 715.
. 715. 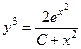 . 716.
. 716. 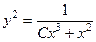 .
.
717. 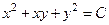 . 718.
. 718. 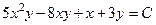 . 719.
. 719. 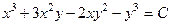 .
.
720. 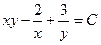 . 721.
. 721. 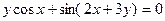 . 722.
. 722. 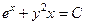 .
.
Дифференциальные уравнения второго порядка
723.-734. Найти общее решение дифференциального уравнения:
723. 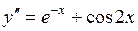 . . | 724. 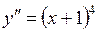 . . |
725. 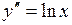 . . | 726. 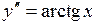 . . |
727. 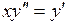 . . | 728. 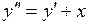 . . |
729. 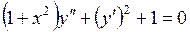 . . | 730. 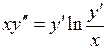 . . |
731. 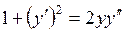 . . | 732. 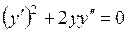 . . |
733. 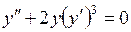 . . | 734. 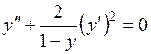 . . |
735.-736. Найти частное решение дифференциального уравнения при заданных условиях:
735. 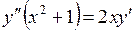 ,
, 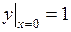 ,
, 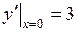 .
.
736. 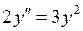 ,
, 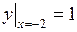 ,
, 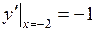 .
.
737.-744. Найти общее решение однородного уравнения:
737. 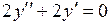 . . | 738. 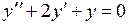 . . | 739. 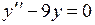 . . |
740. 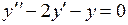 . . | 741. 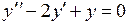 . . | 742. 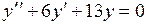 . . |
743. 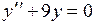 . . | 744. 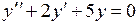 . . |
745.-747. Найти частное решение уравнений:
745. 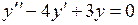 ,
, 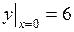 ,
, 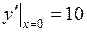 .
.
746. 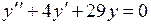 ,
, 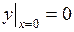 ,
, 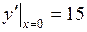 .
.
747. 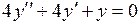 ,
, 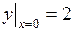 ,
, 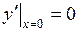 .
.
748. Записать общее решение неоднородного линейного дифференциального уравнения 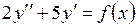 , не вычисляя коэффициенты, если:
, не вычисляя коэффициенты, если:
1) 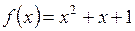 ; ; | 2) 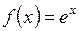 ; ; | 3) 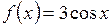 ; ; |
4) 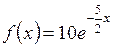 ; ; | 5) 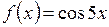 . . |
749. Записать общее решение неоднородного линейного дифференциального уравнения 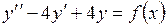 , не вычисляя коэффициенты, если:
, не вычисляя коэффициенты, если:
1) 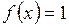 ; ; | 2) 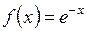 ; ; | 3) 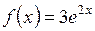 ; ; |
4) 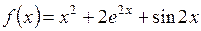 ; ; | 5) 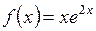 . . |
750.-757. Найти общее решение уравнений:
750. 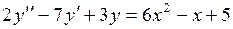 . . | 751. 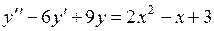 . . |
752. 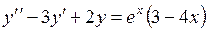 . . | 753. 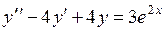 . . |
754. 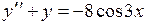 . . | 755. 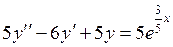 . . |
756. 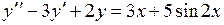 . . | 757. 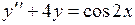 . . |
758.-761. Найти частное решение уравнения:
758. 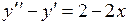 ,
, 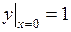 ,
, 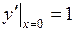 .
.
759. 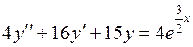 ,
, 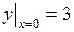 ,
, 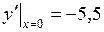 .
.
760. 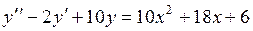 ,
, 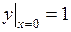 ,
, 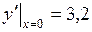 .
.
761. 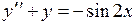 ,
, 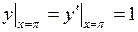 .
.
762.-765. Методом вариации произвольных постоянных решить дифференциальные уравнения:
762. 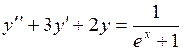 . . | 763. 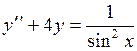 . . |
764. 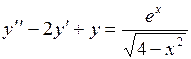 . . | 765. 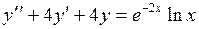 . . |
Ответы.723. 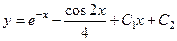 . 724.
. 724. 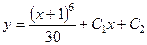 . 725.
. 725. 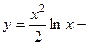
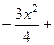
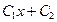 . 726.
. 726. 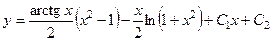 . 727.
. 727. 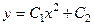 .
.
728. 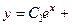
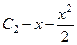 . 729.
. 729. 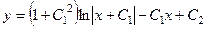 . 730.
. 730. 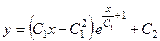 .
.
731. 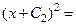
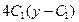 . 732.
. 732. 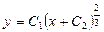 . 733.
. 733. 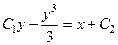 .
.
734. 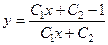 . 735.
. 735. 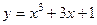 . 736.
. 736. 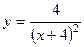 . 737.
. 737. 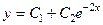 .
.
738. 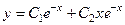 . 739.
. 739. 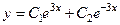 . 740.
. 740. 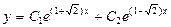 .
.
741. 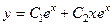 . 742.
. 742. 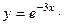
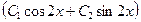 . 743.
. 743. 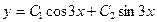 .
.
744. 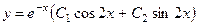 . 745.
. 745. 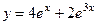 . 746.
. 746. 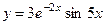 .
.
747. 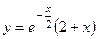 . 748. 1)
. 748. 1) 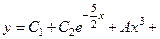
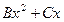 ; 2)
; 2) 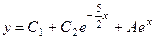 ;
;
3) 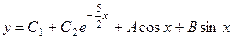 ; 4)
; 4) 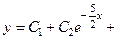
 ; 5)
; 5) 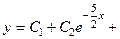
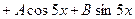 . 749. 1)
. 749. 1) 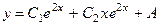 ; 2)
; 2) 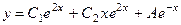 ;
;
3) 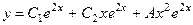 ; 4)
; 4) 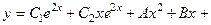
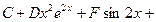
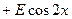 ; 5)
; 5) 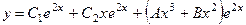 . 750.
. 750. 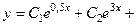
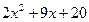 .
.
751. 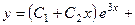
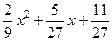 . 752.
. 752. 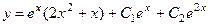 .
.
753. 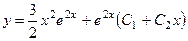 . 754.
. 754. 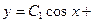
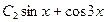 . 755.
. 755. 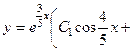
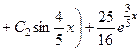 . 756.
. 756. 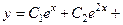
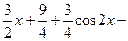
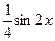 .
.
757. 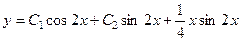 . 758.
. 758. 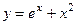 . 759.
. 759. 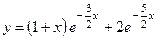 .
.
760. 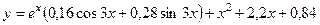 . 761.
. 761. 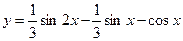 .
.
762. 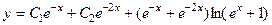 . 763.
. 763. 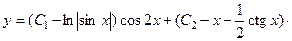
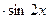 . 764.
. 764. 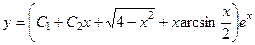 . 765.
. 765. 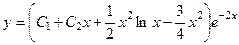
Операционное исчисление
766.-785. Найти изображения функции:
766. 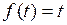 . . | 767. 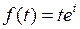 . . |
768. 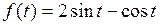 . . | 769. 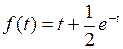 . . |
770. 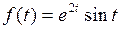 . . | 771. 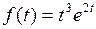 . . |
772. 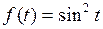 . . | 773. 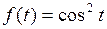 . . |
774. 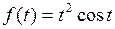 . . | 775. 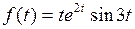 . . |
776. 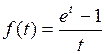 . . | 777. 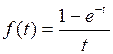 . . |
778. 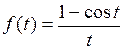 . . | 779. 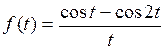 . . |
780. 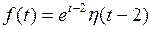 . . | 781. 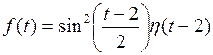 . . |
782. 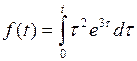 . . | 783. 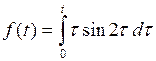 . . |
784. 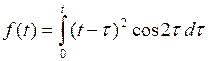 . . | 785. 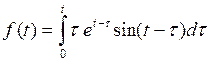 . . |
786.-797. Найти оригинал по изображению:
786. 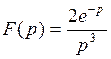 . . | 787. 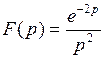 . . |
788. 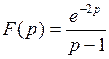 . . | 789. 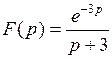 . . |
790. 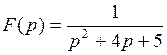 . . | 791. 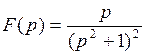 . . |
792. 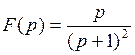 . . | 793. 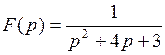 . . |
794. 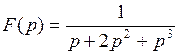 . . | 795. 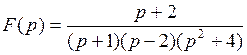 . . |
796. 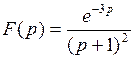 . . | 797. 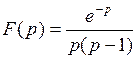 . . |
798.-803. Решить дифференциальные уравнения:
798. 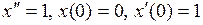 . . | 799. 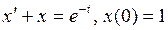 . . |
800. 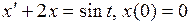 | 801. 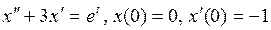 . . |
802. 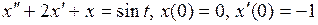 . . | |
803. 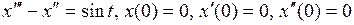 . . |
804.-807. Решить системы дифференциальных уравнений:
804. 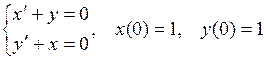 .
.
805. 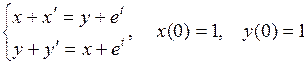 .
.
806. 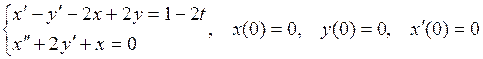 .
.
807. 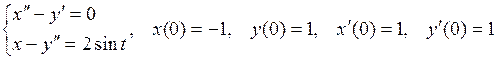 .
.
808.-810. Вычислить несобственный интеграл:
808. 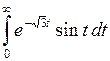 . 809.
. 809. 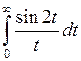 . 810.
. 810. 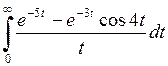 .
.
Ответы. 766. 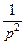 .767.
.767. 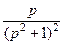 . 768.
. 768. 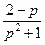 . 769.
. 769. 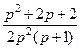 . 770.
. 770. 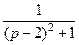 .
.
771. 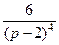 . 772.
. 772. 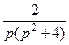 . 773.
. 773. 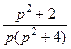 . 774.
. 774. 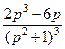 . 775.
. 775. 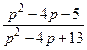 .
.
776. 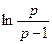 . 777.
. 777. 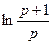 . 778.
. 778. 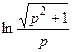 . 779.
. 779. 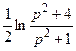 . 780.
. 780. 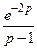 .
.
781. 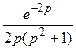 . 782.
. 782. 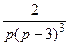 . 783.
. 783. 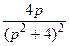 . 784.
. 784. 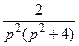 . 785.
. 785. 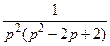 .
.
786. 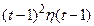 . 787.
. 787. 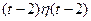 . 788.
. 788. 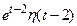 . 789.
. 789. 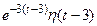 .
.
