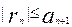Метод вариации произвольной постоянной

y’’+py’+qy=f(x) (1) с пост. коэффициентом. Общее решение ур-я 1 можно записать в виде 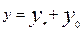, где yo – общее решение соответств. однородного ур-я y’’+py’+qy=0, а y*- частное решение ур-я 1. Одним из способов найти частное реш-е ур-я 1 является метод вариации произвольной постоянной Лагранжа:

y0=C1y1(x)+C2y2(x) y(x),y’(xa) – находимая ф-ция,

y*=c1(x)y1(x)+c2(x)y2(x) с1(x)c2(x) – коэф. ф-ции

c1’(x)y1(x)+c2’(x)y2(x)=0 (2) f(x) – прав. часть ур-ня (1)

c1’(x)y1’(x)+c2’(x)y2’(x)=f(x) (3)

(2) и (3) – система уравнений

Числовой ряд и его сумма. Свойства сходящихся рядов.

Числовым рядомназыв. выражение вида а1+а2+…+аn+…, кот. можно записать 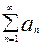(1)

а1, а2 – члены ярда

аn – общий член ряда или n-ый член ряда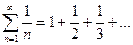

Сумма n-первых членов ряда Sn=a1+a2+..+an назыв. n-ой частичной суммой ряда.

Числовой ряд назыв. сходящимся,если сущ. конечн. предел последоват. Sn=S, S принадлеж. R, S - сумма ряда.

Св-ва сход. рядов:

1.сходимость ряда не нарушается, если произвольным образом изменить (добавить, отбросить) конечное число членов ряда

2. сход. ряда можно почленно умножить на любое число, т.е. общий член множителей можно вынести за знак скобку ,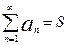

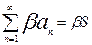
3. сход. ряды можно почленно складывать и отнимать

, ,

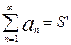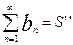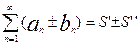
Необходимое условие сходимости числового ряда. Гармонический ряд

Если ряд 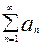- сход., то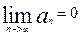

Док-во:

, ,

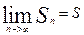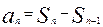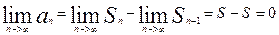
Гармоническим рядом назыв. сумму бесконеч. кол-ва членов обратных последовательным числам нату. ряда. Его обозначают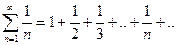

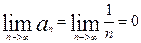
Признаки сравнения сходимости рядов с положительными Членами.

Пусть даны 2 ряда: 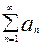(1), 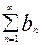(2), an, bn≥0

Признаки сравнения:

Пусть для членов рядов (1) и (2) выполн. неравенство an≤bn, для любых натур чисел, тогда: Если ряд (2) сход., то ряд (1) также сход. , если ряд (1) расх., то (2) расх. тоже

Пусть дял членов рядов (1) и (2) выролн. условие: 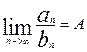, А приндлеж. R A≠0, тогда ряды (1) и (2) сх. или расх. одновременно

Признак Д’Аламбера:

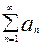(1) , an>0, 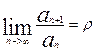, тогда:

Если 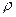<1, то ряд 1 сход., Если 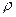>1, то ряд 1 расх. , Если 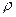=1, то признак не срабатывает

Признак Коши:

1. Если для ряда 1 сущ. 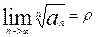, то при 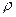<1, ряд 1 сх, а при 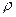>1, ряд 1 расх.

2. Интегральный признак Коши: если для ряда 1 с положит. членами выполн условия:

1)

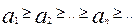
2) сущ. непрерыв. невозраст. ф-ия f(x): an=f(n) для любых натур. n, то ряд 1 инесобств. интеграл 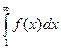сход. или расх одновременно:

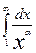α>1 – сход, α<1 – расх.

Знакопеременные и знакочередующиеся ряды. Признак Лейбница.

Числ. ряд назыв. знакопеременным, если он содержит как полож., так и отриц. члены

Пусть 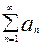(1), а 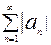(2)

Если ряд 2 сход., то ряд 1 также сход. Если ряд 2 составл. из модулей членов ряда 1, сходится, то ряд 1 назыв. абсолютно сход.

Если ряд 2 расход, а ряд 1 – сход., то говорят, что ряд 1 сходится условно.

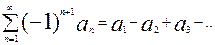(3) – закочередующийся ряд.

Признак Лейбница:

Если для знакочеред. ряда 3 выполн. условие:

1.

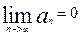
2.

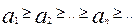
то ряд 3 сход., при этом его сумма S≤a1, а остаток ряда