Дифференциальное исчисление (теория)
1. Если существует предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю произвольным образом, то он называется…
а) производной функции б) дифференциалом функции
в) пределом функции г) скачком
2. Главная часть приращения функции линейная относительно приращения аргумента и отличающая от него на величину бесконечно малую более высокого порядка малости, чем приращение аргумента, называется…
а) дифференциалом функции б) производной функции
в) скачком, г) нормалью к графику функции
3. Функция, которая имеет производную в точке, называется…
а) дифференцируемой в этой точке б) выпуклой в этой точке
в) непрерывной в этой точке г) вогнутой в этой точке
4. Нахождение производной функции называется…
а) дифференцированием этой функции б) транспонированием
в) суперпозицией г) приращением функции
5. Если 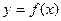 , где
, где 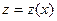 , то…
, то…
а) 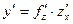 б)
б) 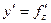 в)
в) 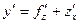 г)
г) 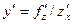
6. Значение производной функции в данной точке 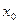 равно…
равно…
а) угловому коэффициенту касательной к графику функции в точке с абсциссой 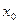 ,
,
б) угловому коэффициенту нормали к графику функции в точке с абсциссой 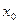 ,
,
в) углу между касательной в точке 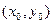 и положительным направлением оси
и положительным направлением оси 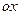 ,
,
г) значению приращения функции в точке 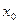 .
.
7. Производная от пути s по времени t равна …
а) скорости v прямолинейного движения материальной точки в момент времени t,
б) ускорению прямолинейного движения точки,
в) угловому коэффициенту прямолинейного движения,
г) 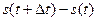 .
.
8. Если функция дифференцируема в точке, то она в этой точке …
а) непрерывна б) имеет минимум в) имеет экстремум г) имеет скачок.
9. Производная от производной функции 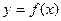 называется …
называется …
а) производной второго порядка б) наложением производных
в) квадратом производной г) произведением производных.
10. Написать уравнение касательной к линии 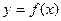 в точке
в точке 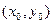
а) 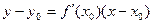 б)
б) 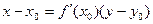
в) 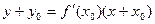 г)
г) 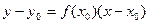
11. Дифференциал от функции 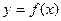 обозначается …
обозначается …
а) 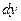 б)
б) 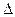 в)
в) 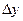 г)
г) 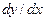 .
.
12. Производная частного двух дифференцируемых функций 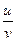 равна …
равна …
а) 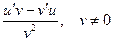 б)
б) 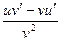 в)
в) 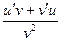 г)
г) 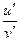 .
.
13. Если функция 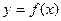 непрерывна на отрезке
непрерывна на отрезке 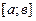 , дифференцируема на интервале
, дифференцируема на интервале 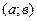 , на концах отрезка принимает равные значения, то внутри отрезка существует, по крайней мере одна точка
, на концах отрезка принимает равные значения, то внутри отрезка существует, по крайней мере одна точка 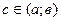 в которой производная равна …
в которой производная равна …
а) 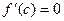 б)
б) 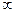 в) не существует г)
в) не существует г) 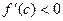 .
.
14. Если функция 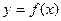 непрерывна на
непрерывна на 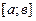 , дифференцируема на
, дифференцируема на 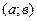 , то существует по крайней мере одна точка
, то существует по крайней мере одна точка 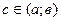 , в которой производная равна …
, в которой производная равна …
а) 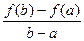 б)
б) 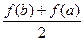 в)
в) 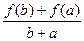 г)
г) 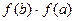 .
.
15. Дифференциалом функции 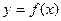 называется главная, линейная относительно
называется главная, линейная относительно 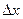 часть приращения функции, равна произведению…
часть приращения функции, равна произведению…
а) производной на приращение независимой переменной;
б) функции на независимую переменную;
в) производной на независимую переменную;
г) функции на приращение независимой переменной.
16. Производная постоянной С равна …
а) 0 б) С в) 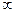 г) 1.
г) 1.
