Рассчет параметров переходных процессов в электрических цепях с двумя реактивными элементами

Определение основных параметров электрической цепи в начале переходного режима и в принужденном режиме

В приведенной схеме, представленной на рисунке 1, были определены начальные и конечные условия для всех токов и напряжений в цепи с нулевыми начальными условиями.

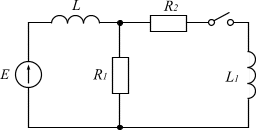
Рисунок 1. Исходная схема для расчета параметров переходного процесса

В таблицу 1 занесены данные для последующий расчётов:

Таблица 1. Данные для расчета

R1, Ом	R2, Ом	С, Ф	С1, Ф	L, Гн	L1, Гн	Е, В
		-	-	1/2

В представленной схеме ненулевые начальные условия, а, следовательно, согласно законам коммутации:

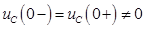
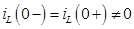
1) Начальные условия ( )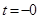

До начала коммутации (при 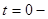) в цепи через индуктивность протекает ток 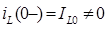. Определим этот ток из эквивалентной схемы для 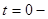. Так как процесс в цепи был установившемся, то для постоянного тока индуктивность заменим перемычкой (рисунок 2).

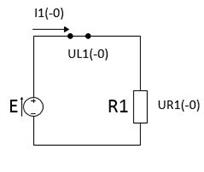
Рисунок 2. Эквивалентная схема цепи для времени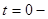

Ток 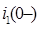равен (по закону Ома):

.

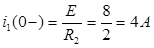Напряжение на индуктивности 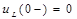, а напряжение на сопротивлении R₁ равно

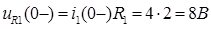
Контроль вычислений.

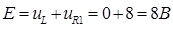– второй закон Кирхгофа выполняется.

Ток 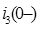и напряжение 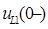равны нулю, так как цепь R₂L₁ до начала коммутации отключена.

2) После коммутации ( 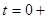) ток в индуктивности скачком измениться не может, поэтому:

.

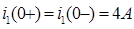Индуктивность в эквивалентной схеме для момента времени 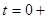заменим источником тока .

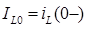Так как 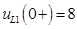, то индуктивность в эквивалентной схеме заменяется разрывом (рисунок 3).

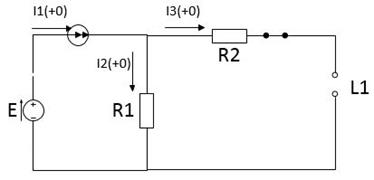
Рисунок 3. Эквивалентная схема цепи для времени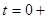

Для рассматриваемой схемы ГНУ:

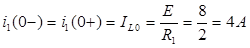
По 1-ому закону Кирхгофа:

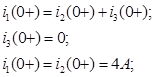
Отсюда следует, что:

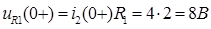
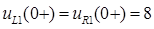
Так как на L₁ обрыв:

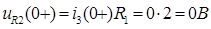
Напряжение на индуктивности

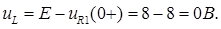
Контроль вычислений.

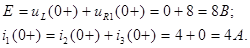
1-й и 2-й законы Кирхгофа выполняются.

3) Конечные условия ( )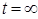

После окончания переходного процесса все токи и напряжения в схеме (рисунок 4) будут постоянными. Так как 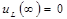, то индуктивность в эквивалентной схеме заменяется перемычкой:

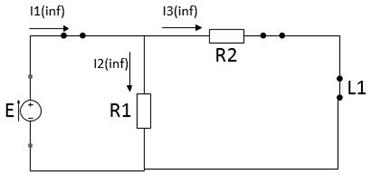
Рисунок 4. Эквивалентная схема цепи для времени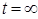

Анализ эквивалентной схемы позволил определить токи и напряжения:

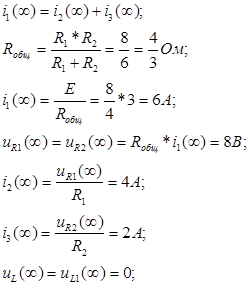
Контроль вычислений.

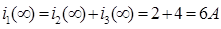– 1-й закон Кирхгофа выполняется.

Таблица 2. Результаты вычислений

t	0 –	0+	¥
i1 , A	4	4	6
i2 , A	0	4	4
i3 , A	0	0	2
uR1 , B	8	8	8
uR2 , B	0	0	8
UL, B	0	0	0
UL1,B	0	8	0

С учетом НУ и КУ можно качественно построить графики (рисунок 5).

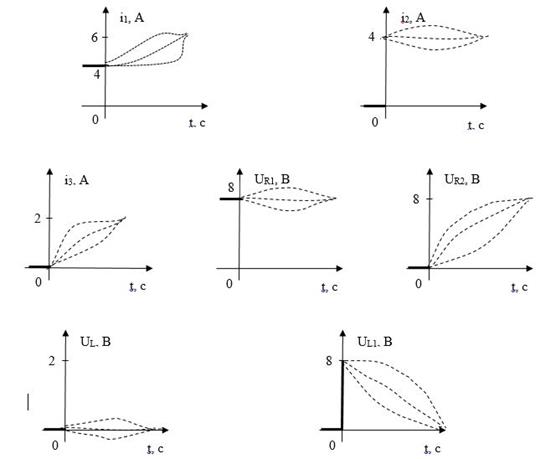
Рисунок 5. Качественные графики

Определение характеристик переходных процессов классическим методом

Для составления дифференциального уравнения был выбран ток 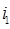. Тогда уравнение в общем виде имеет вид:

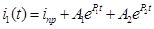
Принужденная составляющая тока 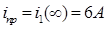, поэтому:

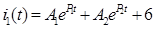
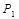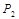Для определения корней характеристического уравнения и была составлена эквивалентная операторная схема цепи (рисунок 6).

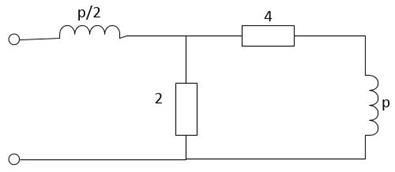
Рисунок 6. Эквивалентная операторная схема цепи

Далее было найдено операторное входное сопротивление и приравнено к нулю ( 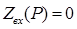). Операторное сопротивление индуктивности 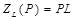, тогда:

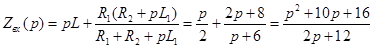
Условие 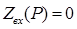выполняется, если числитель равен нулю:

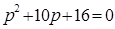
Корни этого уравнения:

;

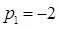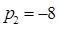
Подставив значения 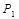и 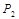в уравнение для 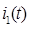, было получено:

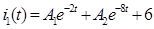
После этого были определены произвольные постоянные 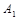и 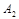. Используя значение самой функции 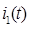и ее производно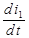й при 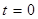, т.е. были учтены начальные условия. Учитывая, что :

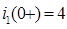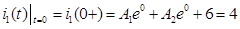
Откуда было получено первое уравнение для нахождения произвольных постоянных:

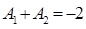
Для получения второго уравнения было найдено значение 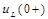при :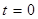

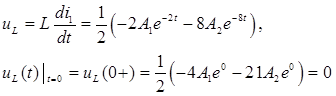
Откуда получается, что второе уравнение для нахождения произвольных постоянных:

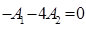
Совместное решение двух уравнений:

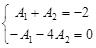
Дает следующие значения произвольных постоянных:

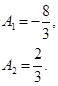
После подстановки произвольных постоянных в выражение для 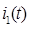получаем:

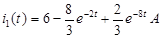
Были произведены контрольные вычисления.

При ,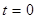

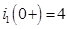
При ,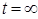

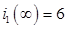
Это показывает, что полученные данные соответствуют данным из таблицы 1.

Расчет остальных токов и напряжений выглядят следующим образом:

А) Напряжение :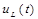

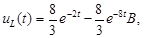
Контроль вычислений:

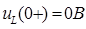
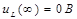
Б) Напряжение :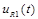

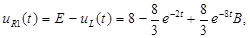
Контроль вычислений:

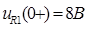
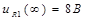
В) Ток :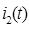

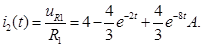
Контроль вычислений:

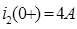
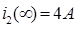
Г) Ток :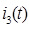

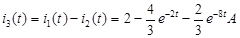
Контроль вычислений:

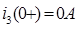
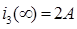
Д) Напряжение :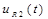

.

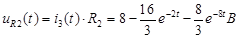Контроль вычислений:

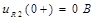
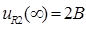
Е) Напряжение :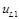

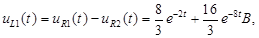
Контроль вычислений:

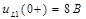
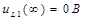
Результаты вычислений:

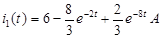
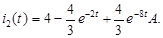
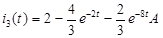
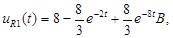
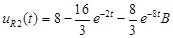
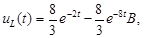
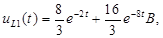
Построенные графики зависимости токов и напряжений от времени по найденным значениям токов и напряжений, представлены в пункте 2.3. Их построение было реализовано с помощью программной среды MatLab.