Метод нахождения всех тупиковых покрытий максимальными интервалами

Мы представляем регулярный способ перечисления всх тупиковых покрытий посредством ограниченного перебора.

Рассмотрим таблицу покрытия. Пусть функция f ( 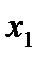,…, 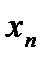) от n переменных имеет s единиц 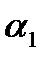,…, , 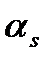и m максимальных интервалов 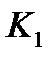,…, 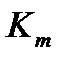. Таблица будет содержать s столбцов, каждый столбец будет соответствовать определенной единице функции и будет содержать m строк , каждая строка соответствует определенному максимальному интервалу.

	,…	,…

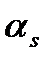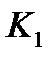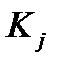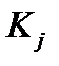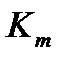На пересечении строки 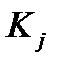и столбца, который соответствует единице функции 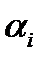поставим интервал 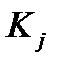, если интервал покрывает 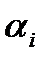. И пусто, если интервал не покрывает единицу 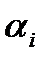. Таким образом, в столбце 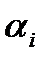непустые элементы в точности все максимальные интервалы, которые покрывают единицу .

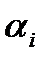Например,

K2

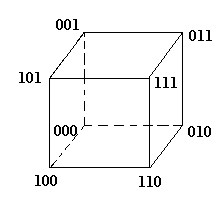
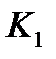-передняя грань 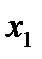, 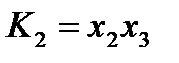- ребро

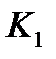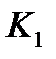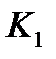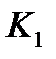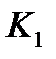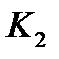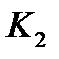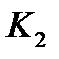Определение:Выборкой называют упорядоченный набор интервалов

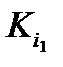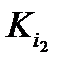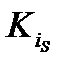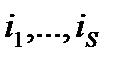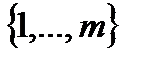, ,…, , Î (каждый индекс принимает значения из множества чисел 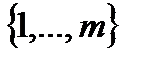, причем значения некоторых индексов могут повторяться), что 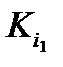есть не нулевой элемент первого столбца , и т. д., 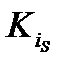- ненулевой элемент последнего s – того столбца .

Например :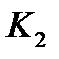

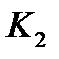
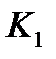
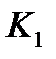
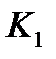
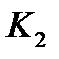
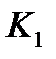
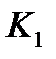
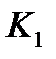
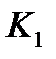- выборки.

Утверждение 1 :Интервалы любой выборки являются покрытием.

Рассмотрим произвольную выборку 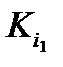, , 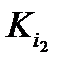… , 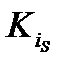. Все интервалы данного множества допустимы, и все единицы функции покрыты.

Действительно, первая единица функции покрыта интервалом 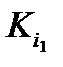, вторая 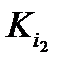, и т. д., последняя единица покрыта .

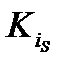Утверждение 2 : Взяв в некотором порядке некоторые интервалы покрытия, можно получить выборку.

Рассмотрим произвольное покрытие. Рассмотрим интервал, который покрывает первую единицу функции, обозначим его .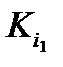

Рассмотрим 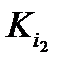и обозначим 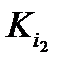, который покрывает вторую единицу функции и т. д. Рассмотрим интервал 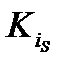, который покрывает последнюю s – ую единицу функции.

Такие интервалы обязательно найдутся, потому что рассматриваемое множество является покрытием.

Тогда полученное множество интервалов 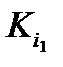, , 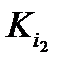… , 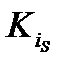является выборкой.

Из этих утверждений следует

Утверждение 3 :Множество тупиковых покрытий содержится среди выборок.

Действительно, каждое тупиковое покрытие есть выборка, которую оно содержит. Интервалы тупикового покрытия можно упорядочить, и при этом получим выборку.

Таким образом, чтобы найти множество тупиковых покрытий нужно найти множество всех выборок, исключить из них нетупиковые выборки.

Множество оставшихся выборок и есть требуемое множество тупиковых покрытий.

Таким образом, мы должны разработатьметод перечисления всех выборок и удаления нетупиковых выборок.