Метод элементарных преобразований для нахождения ранга.
Бывает лучше упростить матрицу, чтобы видеть, какие миноры равны 0 или не равны 0. Как и при вычислении определителей, можно прибавлять к строке другую строку, умноженную на число, то же самое со столбцами. Но при нахождении ранга даже больше возможных действий, чем при вычислении определителя: можно менять местами строки (столбцы), умножать строки (столбцы) на коэффициент. Дело в том, что соответствующие миноры в этом случае меняют знак или умножаются на с, но ведь свойство быть равными 0, либо не равными 0, от этого не меняется!
Если число 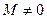 , то
, то 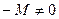 и
и 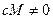 .
.
Пример.
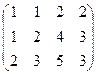
 из 2-й строки вычесть 1-ю, а из 3-й удвоенную 1-ю.
из 2-й строки вычесть 1-ю, а из 3-й удвоенную 1-ю. 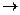
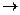
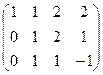
теперь из 3-й строки вычтем 2-ю 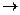
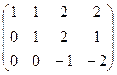 . Ниже главной диагонали получились нули.
. Ниже главной диагонали получились нули.
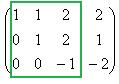
Теперь лучше видно базисный минор порядка 3. Ранг = 3. Если бы оказалось, что последняя строка состоит из нулей, то тогда был бы ответ ранг матрицы = 2.
Ранее упоминали, что матрицы естественным путём связаны с системами векторов.
Определение.Пусть 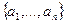 - система векторов.
- система векторов. 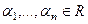 - константы. Тогда вектор
- константы. Тогда вектор 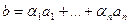 называется линейной комбинацией векторов
называется линейной комбинацией векторов 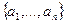 .
.
(А если все коэффициенты = 1, то это просто сумма векторов).
Пример. 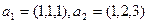 . Пусть коэффициенты 2 и 1. Линейная комбинация это вектор (3,4,5):
. Пусть коэффициенты 2 и 1. Линейная комбинация это вектор (3,4,5):
2(1,1,1)+1(1,2,3) = (3,4,5).
В пространстве, рассмотрим 3 вектора: (1,0,0), (0,1,0) и (0,0,1). Любой вектор 3-мерного пространства можно представить как линейную комбинацию этих трёх векторов.
* Если все коэффициенты 0, то линейная комбинация есть 0 вектор в любом случае, какими бы ни были векторы.
* Допустим, что взяты векторы (1,0) и (-1,0). Если их сложить, то получим (0,0). Видим, что бывают ситуации, когда линейная комбинация ненулевых векторов - это нулевой вектор, даже если ненулевые коэффициенты! Аналогичная ситуация, если вектор с есть a+b, тогда a+b-c = 0. В связи с этим возникает определение линейно-зависимой и линейно-независимой системы векторов.
Определение.Если из равенства 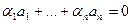 следует, что
следует, что 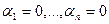 , то система векторов называется линейно-независимой системой (ЛНС). Если же существует набор ненулевых коэффициентов
, то система векторов называется линейно-независимой системой (ЛНС). Если же существует набор ненулевых коэффициентов 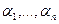 , такой, что линейная комбинация = 0, то система называется линейно-зависимой системой (ЛЗС).
, такой, что линейная комбинация = 0, то система называется линейно-зависимой системой (ЛЗС).
Примеры. * Если вектор с есть a+b, тогда a+b-c = 0. Коэффициенты 1,1,-1.
* если 2 вектора коллинеарны, то они образуют ЛЗС.
* если нулевой вектор принадлежит системе, то она ЛЗС. Это доказывается так: коэффициент при 0-векторе может быть любым числом, т.к. он всё равно не влияет на сумму векторов, а значит, существует набор коэффициентов, в котором не все нули, и значит, формально по определению такая система векторов ЛЗС.
Теорема. Система линейно зависима 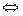 хотя бы один из векторов этой системы является линейной комбинацией остальных.
хотя бы один из векторов этой системы является линейной комбинацией остальных.
Идея доказательства. Необходимость. Если система ЛЗС, то хотя бы у какого-то вектора есть ненулевой коэффициент, тогда это слагаемое можно перенести в другую сторону и разделить всё равенство на этот коэффициент.
Достаточность. Если вектор выражен через остальные, его можно перенести в другую сторону равенства, ко всем остальным векторам, то есть в записи 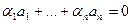 ему будет соответствовать коэффициент (-1).
ему будет соответствовать коэффициент (-1).
Так, если выражен 1-й вектор, то 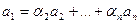 , тогда
, тогда 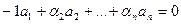 .
.
Определение. Максимальная линейно-независимая подсистема называется базисом системы векторов, а число векторов в ней - рангом системы векторов.
Пример. Если в плоскости есть 2 неколлинеарных вектора, и добавлены 100 векторов в той же плоскости, r = 2.
* 3 вектора, из которых 2 коллинеарны. Ранг = 2.
* 3 вектора, из которых все 3 коллинеарны. Ранг = 1.
Как видим, было 2 подхода к понятию ранга: ранг системы (число векторов в максимальной независимой подсистеме) и ранг матрицы (порядок наибольшего невырожденного минора). На самом деле, не случайно используется одно и то же слово: если матрицу мысленно разрезать на строки, будет система векторов, и у неё ранг точно такой же, как был у исходной матрицы. Аналогичное верно и для системы столбцов.
Теорема (о ранге матрицы). Ранг матрицы равен рангу системы её строк (столбцов).
