Элементы векторной алгебры и аналитической геометрии
Учебно-методический комплекс
Часть 3
Методические указания
К выполнению контрольных работ
Для студентов всех специальностей и направлений
Заочной формы обучения
УФА 2012
УДК 51(076.1)
М 54
Математика. УМК. Часть 3: Методические указания по выполнению контрольных работ для студентов заочной формы обучения / Сост.: Р.Р. Сафин, Г.А.Ларичева, М.А. Богданова. – Уфа: Уфимская государственная академия экономики и сервиса, 2012. – 79 с.
Приведены контрольные задания и решения типовых задач по дисциплине «Математика».
Предназначены для студентов всех специальностей и направлений заочной формы обучения.
Рецензент: Бакусова С.М., канд. физ.-мат. наук, доцент кафедры «Экономическая теория и мировая экономика» Уфимской государственной академии экономики и сервиса.
© Сафин Р.Р., Ларичева Г.А.,
Богданова М.А., 2012
© Уфимская государственная
академия экономики и сервиса, 2012
СОДЕРЖАНИЕ
Рекомендации по выполнению и оформлению контрольных работ 3
Введение 4
Контрольные задания 4
Список литературы 76
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Перед выполнением контрольного задания студент должен изучить соответствующие разделы курса по пособиям и учебникам. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию на кафедре высшей математики.
При выполнении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
1. Контрольную работу следует выполнять в тетради, отдельной для каждой работы, чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины. В конце работы следует проставить дату её выполнения и расписаться.
3. В тетради должны быть решены все задачи контрольной работы строго в соответствии со своим вариантом. Контрольные работы, содержащие не все задачи, а также содержащие задачи не своего варианта, не зачитываются.
4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.
5. Перед решением каждой задачи нужно выписать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера. Например, условие задачи 1 должно быть переписано так: Даны вершины А(1;1), В(7;4), С(4;5) треугольника. Найти: 1) длину стороны АВ и т.д.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента.
Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок.
В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
Рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Прорецензированную контрольную работу вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, студент представляет к защите.
ВВЕДЕНИЕ
В каждом семестре выполняется одна контрольная работа. Студент должен решить задачи своего варианта, который определяется по последней цифре номера зачетной книжки студента, например: если № зачетной книжки заканчивается на 2, то студент выполняет задания 1.2, 2.2, 3.2, 4.2, 5.2, 6.2, 7.2. В задачах 32-36 данные в задачах определяются по последним трем цифрам номера зачетной книжки студента.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Элементы векторной алгебры и аналитической геометрии
Задача 1.Даны векторы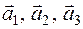 
и 
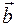в некотором базисе трехмерного пространства. Показать, что векторы 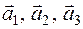образуют базис данного трехмерного пространства и найти координаты вектора 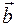в этом базисе.
1.1.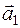 
(1;2;3), 
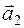(-1;3;2), 
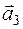(7;-3;5), 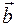(6;10;17).
1.2. 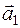(4;7;8), 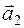(9;1;3), 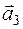(2;-4;1), 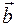(1;-13;-13).
1.3. 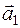(8;2;3), 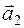(4;6;10), 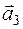(3;-2;1), 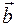(7;4;11).
1.4. 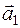(10;3;1), 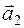(1;4;2), 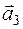(3;9;2), 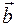(19;30;7).
1.5. 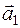(2;4;1), 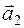(1;3;6), 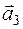(5;3;1), 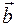(24;20;6).
1.6. 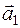(1;7;3), 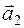(3;4;2), 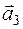(4;8;5), 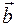(7;32;14).
1.7. 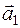(1;-2;3), 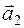(4;7;2), 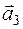(6;4;2), 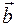(14;18;6).
1.8. 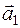(1;4;3), 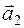(6;8;5), 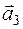(3;1;4), 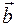(21;18;33).
1.9. 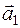(2;7;3), 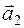(3;1;8), 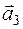(2;-7;4), 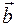(16;14;27).
1.10. 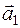(7;2;1), 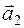(4;3;5), 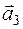(3;4;-2), 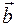(2;-5;-13).
Задача 2.Даны векторы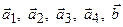 
. Показать, что векторы 
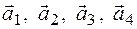образуют базис четырехмерного пространства и найти координаты вектора 
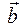в этом базисе.
2.1.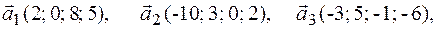 
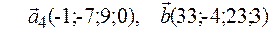
2.2.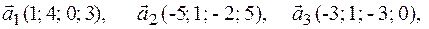 
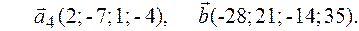
2.3.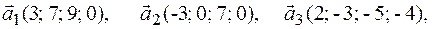 
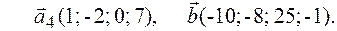
2.4.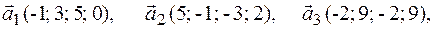 
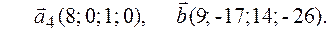
2.5.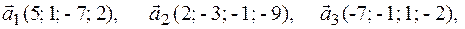 
2.6.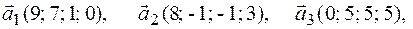 
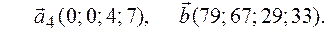
2.7.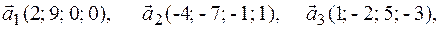 
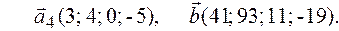
2.8.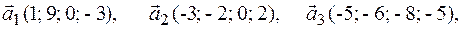 
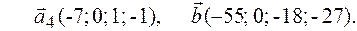
2.9.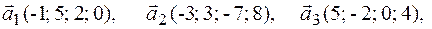 
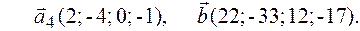
2.10.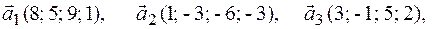 
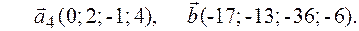
Задача 3. Даны вершины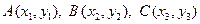 
треугольника. Найти: 1) длину стороны 
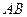; 2) внутренний угол 
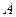в радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину 
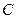; 4) уравнение медианы, проведенной через вершину 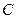; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины 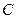; 7) систему неравенств, определяющих треугольник 
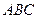. Сделать чертеж.
3.1.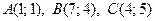 
.
3.2.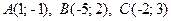 
.
3.3.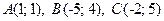 
.
4.4.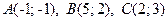 
.
3.5.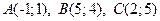 
.
3.6.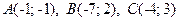 
.
3.7.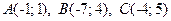 
.
3.8.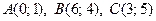 
.
3.9.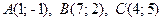 
.
3.10.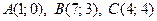 
.
Задача 4.Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 
3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
4.1. А1(4;2;5), А2(0;7;2), А3(0;2;7), А4(1;5;0).
4.2. А1(4;4;10), А2(4;10;2), А3(2;8;4), А4(9;6;4).
4.3. А1(4;6;5), А2(6;9;4), А3(2;10;10), А4(7;5;9).
4.4. А1(3;5;4), А2(8;7;4), А3(5;10;4), А4(4;7;8).
4.5. А1(10;6;6), А2(-2;8;2), А3(6;8;9), А4(7;10;3).
4.6. А1(1;8;2), А2(5;2;6), А3(5;7;4), А4(4;10;9).
4.7. А1(6;6;5), А2(4;9;5), А3(4;6;11), А4(6;9;3).
4.8. А1(7;2;2), А2(5;7;7), А3(5;3;1), А4(2;3;7).
4.9. А1(8;6;4), А2(10;5;5), А3(5;6;8), А4(8;10;7).
4.10. А1(7;7;3), А2(6;5;8), А3(3;5;8), А4(8;4;1).