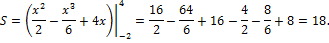Задание 2. Найти неопределенные интегралы
КОНТРОЛЬНАЯ РАБОТА
За 2 семестр по дисциплине «Математический анализ»
Для студентов дневного отделения,
обучающихся по направлению «Экономика»
Контрольная работа является зачетной работой. Она должна быть выполнена студентом самостоятельно, согласно индивидуальному варианту, который определяется преподавателем. Решения всех задач и пояснения к ним должны быть достаточно подробными. Работа выполняется студентом самостоятельно и оформляется в отдельной тетради в клетку или, в случае использования прикладных программ, распечатывается и сшивается в одну папку. Титульный лист работы должен соответствовать установленному образцу, который можно взять в информационном центре.
Задание 1. Найти радиус, интервал и область сходимости ряда
Вариант № 1: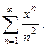 
Вариант №2: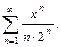 
Вариант №3: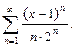 
Вариант №4: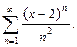 
Вариант №5: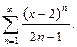 
Вариант №6: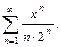
Вариант №7: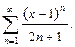 
Вариант №8: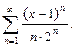
Вариант №9: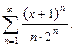 
Вариант №10: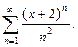 
Указания к выполнению Задания 2
Найдем радиус, интервал и область сходимости ряда: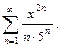 
Запишем коэффициент данного ряда: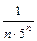 
. Найдём радиус сходимости данного ряда:
.
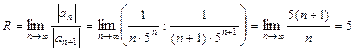Интервал сходимости данного ряда будет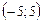 
. Проверим поведение ряда в конечных точках данного интервала.
Пусть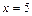 
. Получим ряд 
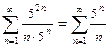. Проверим его сходимость по признаку Даламбера:
.
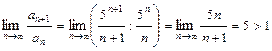Ряд расходится, следовательно, точка 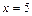не принадлежит области сходимости.
Пусть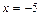 
. Получим знакочередующийся ряд 
.
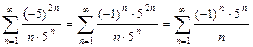Расходимость полученного ряда устанавливается с помощью признака Лейбница (не выполняется первое условие). То есть, точка 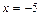также не входит в область сходимости.
Итак, область сходимости данного ряда – промежуток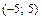 
.
Задание 2. Найти неопределенные интегралы
Вариант № 1: 1)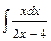 
; 2) 
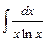; 3)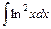 
.
Вариант №2: 1)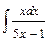 
; 2) 
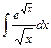; 3)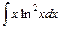 
.
Вариант №3: 1)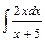 
; 2) 
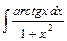; 3)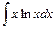 
.
Вариант №4: 1)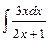 
; 2) 
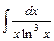; 3)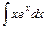 
.
Вариант №5: 1) 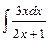; 2) 
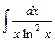; 3)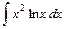 
.
Вариант №6: 1)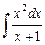 
; 2) 
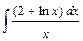; 3)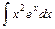 
.
Вариант №7: 1)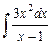 
; 2) 
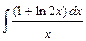; 3)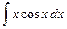 
.
Вариант №8: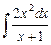 
; 2) 
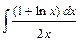; 3)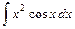 
.
Вариант №9: 1)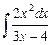 
; 2) 
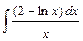; 3)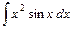 
.
Вариант №10: 1)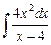 
; 2) 
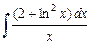; 3)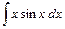 
.
Указания к выполнению Задания 2
1) 
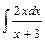. Преобразуем подынтегральное выражение:
.
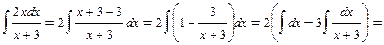
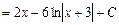2) 
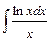. Применим метод замены переменной:
.
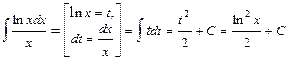3) 
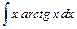. Применим формулу интегрирования по частям: 
.
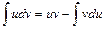В данном случае: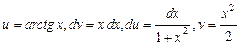 
. Подставляя эти выражения в формулу, получим:
.
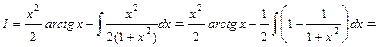
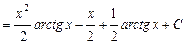Задание 3. Вычислить площадь фигуры, ограниченной параболой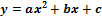 
и прямой 
.
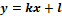Сделать чертеж.
Вариант № 1: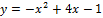 
и 
.
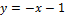Вариант № 2: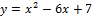 
и 
.
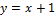Вариант № 3: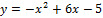 
и 
.
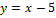Вариант № 4: 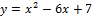и 
.
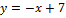Вариант № 5: 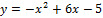и 
.
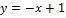Вариант № 6: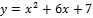 
и 
.
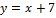Вариант № 7: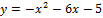 
и .
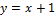Вариант № 8: 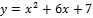и .
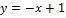Вариант № 9: 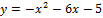и 
.
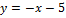Вариант № 10: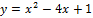 
и .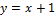
Указания к выполнению Задания 3
Вычислим площадь фигуры, ограниченной линиям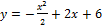и
и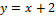 
(рис. 14).
Заметим, что графиком функции 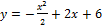является парабола, ветви которой направлены вниз (т.к. коэффициент при 
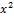меньше нуля); вершина параболы находится из формулы 
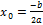, т.е. задается точкой (2; 8). График функции 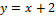– прямая, проходящая через точки (0;2) и (1;3).
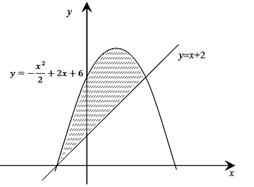
Рис. 14.
Найдем точки пересечения заданных линий. Для этого решим систему уравнений:
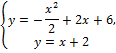
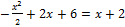или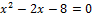 
.
Находим: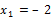 
, 
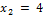. Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках 
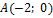и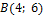 
.
Эти линии образуют замкнутую фигуру, площадь которой вычислим по формуле:
.
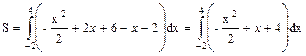По формуле Ньютона-Лейбница находим:
