Лекция 6. Предел функции. Непрерывность функции
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ.
Лекция 5. Функции одной переменной и числовые последовательности.
План лекции.
5.1. Определение функции. Числовые последовательности.
5.2. Классификация функций.
5.3. Способы задания функций. Условие существования обратной функции. Понятие сложной функции.
5.4. Основные элементарные функции, их свойства и графики.
5.5. Преобразования прямоугольной системы координат.
5.6. Построение графиков функций с помощью геометрических преобразований.
5.1
При изучении природных и технических процессов исследователи сталкиваются с величинами, одни из которых сохраняют одно и то же числовое значение – они называются постоянными, а другие принимают различные числовые значения и называются переменными.
В практических задачах изменение переменной величины обычно связано с изменением одной или нескольких других переменных величин.
Например, путь пройденный телом с постоянной скоростью, прямо пропорционален времени движения: 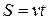 .
.
Этой формулой выражена зависимость переменной 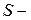 пути, пройденного телом, от переменной
пути, пройденного телом, от переменной 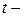 времени движения. Переменные
времени движения. Переменные 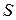 и
и 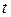 не могут принимать произвольные значения независимо друг от друга. Придав определенное значение переменной
не могут принимать произвольные значения независимо друг от друга. Придав определенное значение переменной 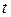 , мы тем самым единственным образом определим значение переменной
, мы тем самым единственным образом определим значение переменной 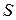 .
.
Если каждому значению, которое может принять переменная 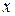 , по некоторому правилу или закону ставится в соответствие одно определенное значение переменной
, по некоторому правилу или закону ставится в соответствие одно определенное значение переменной 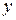 , то говорят, что
, то говорят, что 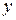 есть функция от
есть функция от 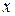 , обозначают
, обозначают 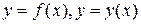 и т.п. Переменная
и т.п. Переменная 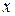 называется независимой переменной или аргументом, а переменная
называется независимой переменной или аргументом, а переменная 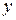 - зависимой переменной или функцией.
- зависимой переменной или функцией.
Совокупность всех значений аргумента 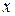 , для которых функция
, для которых функция 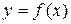 определена, называется областью определения этой функции. Обозначается
определена, называется областью определения этой функции. Обозначается 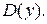
Совокупность всех значений, принимаемых переменной 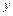 называется областью значений функции. Обозначается
называется областью значений функции. Обозначается 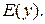
Графиком функции 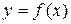 называется изображение на координатной плоскости множества пар
называется изображение на координатной плоскости множества пар 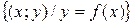 .
.
Не всякое множество точек координатной плоскости является графиком функции. Для того, чтобы множество точек являлось графиком функции необходимо и достаточно, чтобы прямая параллельная оси 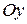 пересекалась с графиком не более чем в одной точке.
пересекалась с графиком не более чем в одной точке.
Значения аргумента, при которых функция обращается в ноль, называются корнями или нулями функции, т.е. если 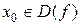 и
и 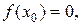 то
то 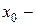 ноль функции. Корни функции – это точки пересечения ее графика с осью абсцисс.
ноль функции. Корни функции – это точки пересечения ее графика с осью абсцисс.
Числовые промежутки, на которых функция сохраняет свой знак, т.е. остается положительной или отрицательной называются интервалами знакопостоянства функции.
Для нахождения интервалов знакопостоянства функции
1) находят область определения функции;
2) находят нули функции;
3) разбивают область определения нулями функции на промежутки;
4) определяют знак функции на каждом полученном промежутке (с помощью метода интервалов).
Частным случаем функций являются числовые последовательности. Бесконечной числовой последовательностью (или просто числовой последовательностью) называется функция 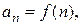 определенная на множестве натуральных чисел. Значения последовательности
определенная на множестве натуральных чисел. Значения последовательности 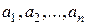 называются ее членами. Обозначается числовая последовательность
называются ее членами. Обозначается числовая последовательность 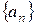 .
. 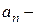 называется общим членом числовой последовательности. Зная общий член, можно получить любой член этой последовательности, придавая
называется общим членом числовой последовательности. Зная общий член, можно получить любой член этой последовательности, придавая 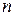 какое-то значение.
какое-то значение.
Например,
1) 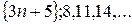 , 2)
, 2) 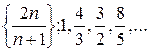 ,
,
3) 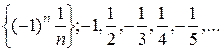
Для числовой последовательности, как и для любой функции, можно построить график. Он состоит из отдельных точек, расположенных справа от оси 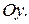
5.2
Функция 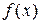 называется возрастающей на данном числовом множестве, если большему значению аргумента
называется возрастающей на данном числовом множестве, если большему значению аргумента 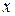 из этого множества соответствует большее значение
из этого множества соответствует большее значение 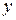 , т.е. если
, т.е. если 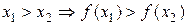 . Аналогично, функция называется убывающей на некотором множестве, если большему значению аргумента соответствует меньшее значение функции, т.е. если
. Аналогично, функция называется убывающей на некотором множестве, если большему значению аргумента соответствует меньшее значение функции, т.е. если 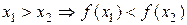 . Функция только возрастающая или только убывающая на данном множестве называется монотонной на этом множестве.
. Функция только возрастающая или только убывающая на данном множестве называется монотонной на этом множестве.
Числовая последовательность 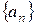 называется невозрастающей (неубывающей), если для любого номера
называется невозрастающей (неубывающей), если для любого номера 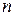 справедливо неравенство
справедливо неравенство 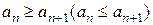 .
.
Если 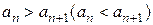 , то последовательность
, то последовательность 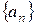 - убывающая (возрастающая). Невозрастающие и неубывающие последовательности называются монотонными.
- убывающая (возрастающая). Невозрастающие и неубывающие последовательности называются монотонными.
Пусть область определения функции 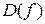 симметрична относительно начала координат, т.е. если
симметрична относительно начала координат, т.е. если 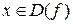 , то и
, то и 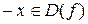 . Функция
. Функция 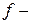 называется четной, если
называется четной, если 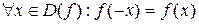 , и функция называется нечетной, если
, и функция называется нечетной, если 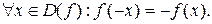 График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Функция 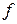 называется периодической, если
называется периодической, если
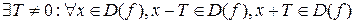 и
и 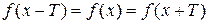 . В этом случае число
. В этом случае число 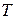 называется периодом функции
называется периодом функции 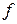 . Если
. Если 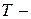 период функции, то
период функции, то 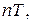 где
где 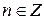 тоже является периодом функции. Поэтому рассматривают функции с наименьшим, положительным периодом.
тоже является периодом функции. Поэтому рассматривают функции с наименьшим, положительным периодом.
Например, для функций 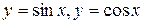 наименьший положительный период
наименьший положительный период 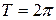 , а для функций
, а для функций 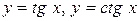 наименьший положительный период
наименьший положительный период 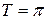 . Существуют и другие периодические функции.
. Существуют и другие периодические функции.
Числовая функция 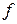 , определенная на множестве
, определенная на множестве 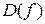 называется ограниченной, если существует такое положительное число
называется ограниченной, если существует такое положительное число 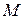 , что
, что 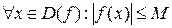 .
.
Запишем указанное в определении неравенство в развернутом виде: 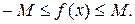 Из полученного двойного неравенства следует, что график ограниченной функции располагается в полосе между двумя прямыми параллельными оси
Из полученного двойного неравенства следует, что график ограниченной функции располагается в полосе между двумя прямыми параллельными оси 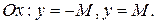 Например
Например 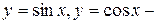 ограниченные функции.
ограниченные функции.
Числовая функция 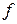 , определенная на множестве
, определенная на множестве 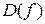 называется ограниченной сверху (снизу), если существует такое число
называется ограниченной сверху (снизу), если существует такое число 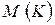 ,что
,что 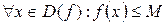
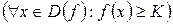 .
.
Последовательность 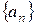 называется ограниченной сверху (снизу), если существует такое число
называется ограниченной сверху (снизу), если существует такое число 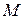 , что
, что 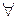 номера
номера 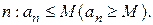 Последовательность, ограниченная и сверху и снизу, называется ограниченной.
Последовательность, ограниченная и сверху и снизу, называется ограниченной.
5.3
Существует три основных способа задания функции.
1-ый способ: аналитический – это задание функции при помощи формул.
Функция может быть задана явно, если уравнение, при помощи которого задается функция разрешено относительно 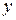 . Например,
. Например, 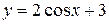 .
.
Если уравнение, при помощи которого задается функция не разрешено относительно 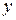 , то говорят, что функция задана в неявном виде. Например,
, то говорят, что функция задана в неявном виде. Например, 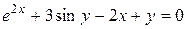 .
.
Функция может быть также задана параметрически. Если даны два уравнения
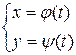 , (5.1)
, (5.1)
где 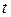 принимает значения, содержащиеся на отрезке
принимает значения, содержащиеся на отрезке 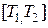 , причем каждому значению
, причем каждому значению 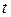 соответствуют значения
соответствуют значения 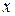 и
и 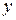 (функции
(функции 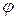 и
и 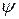 предполагаем однозначными), то каждому значению
предполагаем однозначными), то каждому значению 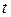 будет соответствовать определенная точка плоскости. Когда
будет соответствовать определенная точка плоскости. Когда 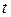 изменяется от
изменяется от 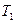 до
до 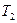 , эта точка на плоскости описывает некоторую кривую. Тогда уравнения (5.1) называются параметрическими уравнениями кривой,
, эта точка на плоскости описывает некоторую кривую. Тогда уравнения (5.1) называются параметрическими уравнениями кривой, 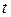 - параметром, а способ задания кривой уравнениями (5.1) – параметрическим.
- параметром, а способ задания кривой уравнениями (5.1) – параметрическим.
2-ой способ: табличный способ – широко используется в различных экспериментах и наблюдениях. Этот способ прост в обращении, но функция задается не для всех значений аргумента.
3-ий способ: графический способ задания функции – функция задается графиком, этот способ нагляден, используется при работе самопишущих приборов (кардиограф).
Пусть функция 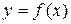 – монотонна в своей области определения, тогда
– монотонна в своей области определения, тогда 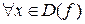 соответствует единственное
соответствует единственное 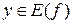 и наоборот
и наоборот 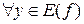 соответствует единственное
соответствует единственное 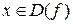 . Тогда можно построить функцию, определенную на множестве
. Тогда можно построить функцию, определенную на множестве 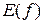 со значениями во множестве
со значениями во множестве 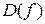 , обозначим ее
, обозначим ее 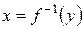 . Такая функция называется обратной для функции
. Такая функция называется обратной для функции 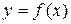 . Уступая традиции, обозначим значение аргумента у обратной функции через
. Уступая традиции, обозначим значение аргумента у обратной функции через 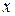 , а значение функции через
, а значение функции через 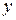 , т.е. пусть
, т.е. пусть 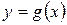 - обозначение обратной функции для функции
- обозначение обратной функции для функции 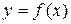 . Тогда функции
. Тогда функции 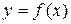 и
и 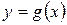 являются взаимно-обратными функциями, для них справедливо, что
являются взаимно-обратными функциями, для них справедливо, что 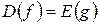 и
и 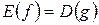 , а графики взаимно-обратных функций симметричны относительно прямой
, а графики взаимно-обратных функций симметричны относительно прямой 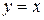 .
.
Пусть переменная 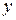 зависит от переменной
зависит от переменной 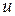 , которая в свою очередь зависит от переменной
, которая в свою очередь зависит от переменной 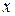 , т.е.
, т.е. 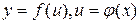 .Тогда при изменении
.Тогда при изменении 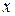 будет меняться
будет меняться 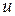 , а потому будет меняться и
, а потому будет меняться и 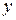 . Значит,
. Значит, 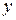 является функцией от
является функцией от 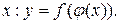 Эта функция называется сложной функцией или суперпозицией функций
Эта функция называется сложной функцией или суперпозицией функций 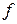 и
и 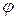 .
.
5.4
Функции:
постоянная 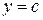 (константа), степенная
(константа), степенная 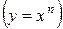 , показательная
, показательная 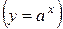 , логарифмическая
, логарифмическая 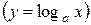 ,
,
тригонометрические 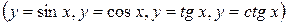 ,
,
обратные тригонометрические функции
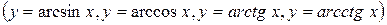
– называются основными элементарными функциями.
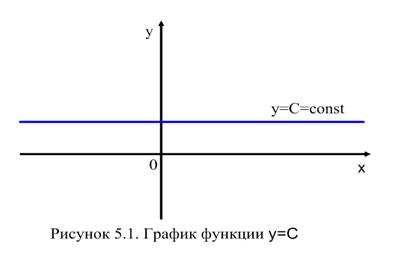
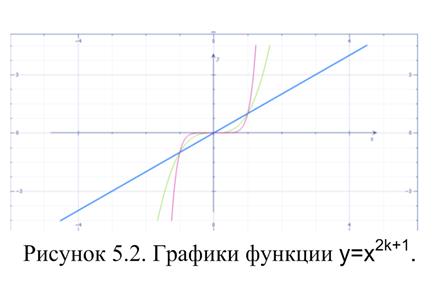
Функция вида 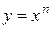 , где
, где 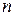 - натуральное, называется степенной функцией с натуральным показателем. Определяют также степенную функцию с рациональным показателем. Свойства этих функций представлены в таблице 5.1, графики на рисунках 5.2 – 5.5.
- натуральное, называется степенной функцией с натуральным показателем. Определяют также степенную функцию с рациональным показателем. Свойства этих функций представлены в таблице 5.1, графики на рисунках 5.2 – 5.5.
Таблица 5.1. Степенная функция для различных показателей
| Функция | 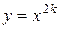 , , 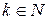 | 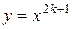 , , 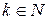 | 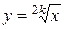 , , 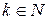 | 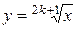 , , 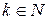 |
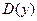 | R | R | 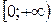 | R |
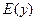 | 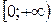 | R | 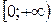 | R |
Точки пересечения с осью 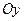 | 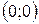 | 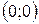 | 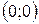 | 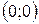 |
Точки пересечения с осью 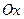 (нули функции) (нули функции) | 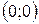 | 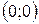 | 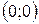 | 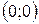 |
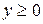 при при 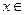 | R | 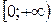 | R | 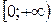 |
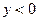 при при 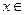 | - | 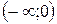 | - | 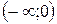 |
| Производная функции | 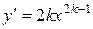 | 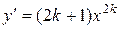 | 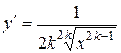 | 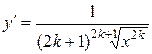 |
| Интервалы возрастания функции | 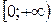 | R | 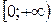 | R |
| Интервалы убывания функции | 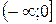 | - | - | - |
| Точки максимума функции | - | - | - | - |
| Максимумы функции | - | - | - | - |
| Точки минимума функции | - | - | - | |
| Минимумы функции | - | - | - | |
| Чётность | чётная | нечётная | ни чётная, ни нечётная | нечётная |
Функция 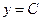 , сохраняющая постоянное значение, называется постоянной (константой). При
, сохраняющая постоянное значение, называется постоянной (константой). При 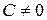 функция является чётной. При
функция является чётной. При 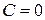 функция является и чётной и нечётной. Свойства этой функции приведены в таблице 5.2, график на рисунке 5.1.
функция является и чётной и нечётной. Свойства этой функции приведены в таблице 5.2, график на рисунке 5.1.
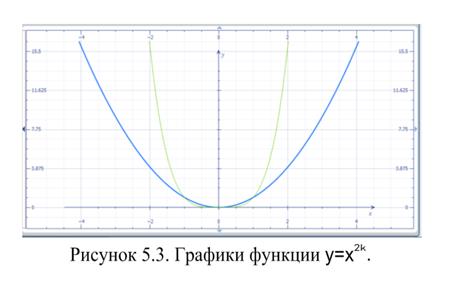
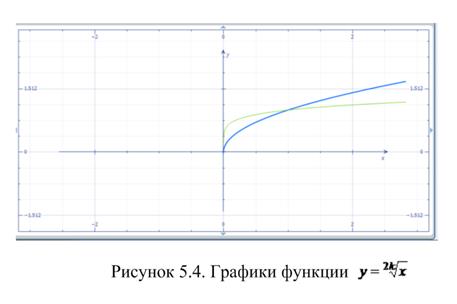
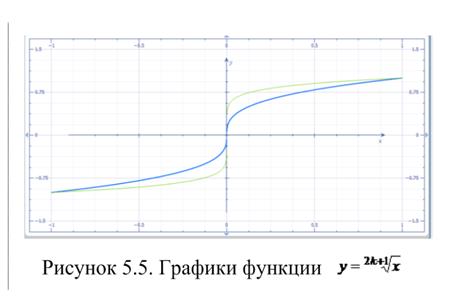
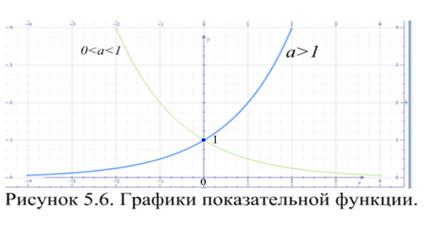
Функция вида 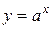 , где
, где 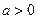 и
и 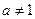 , называется показательной функцией (таблица 5.2, рисунок 5.6). Эта функция каждому действительному числу
, называется показательной функцией (таблица 5.2, рисунок 5.6). Эта функция каждому действительному числу 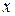 ставит в соответствие число
ставит в соответствие число 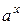 .
.
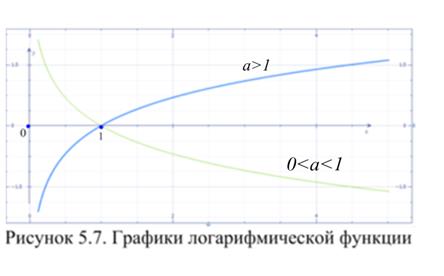
Для показательной функции определяется обратная функция – логарифмическая. Функция вида 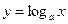 , где
, где 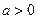 и
и 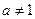 , называется логарифмической (таблица 5.2, рисунок 5.7). Эта функция каждому положительному значению аргумента ставит в соответствие его логарифм по основанию
, называется логарифмической (таблица 5.2, рисунок 5.7). Эта функция каждому положительному значению аргумента ставит в соответствие его логарифм по основанию 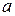 . Функции
. Функции 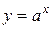 и
и 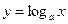 не являются ни чётными, ни нечётными.
не являются ни чётными, ни нечётными.
Таблица 5.2. Показательная, логарифмическая и постоянная функции
| Функция | 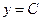 | 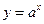 при при 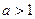 | 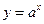 при при 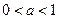 | 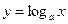 при при 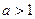 | 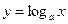 при при 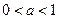 |
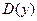 | R | R | R | 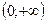 | 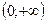 |
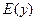 | 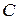 | 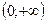 | 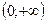 | R | R |
Точки пересечения с осью 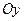 | 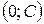 | 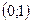 | 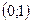 | - | - |
Точки пересечения с осью 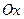 (нули функции) (нули функции) | при 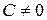 точек нет точек нет | - | - | 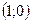 | 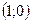 |
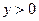 при при 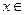 | сохраняет знак С | 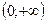 | 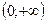 | 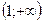 | 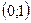 |
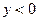 при при 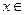 | - | - | 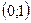 | 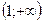 | |
| Производная функции | 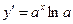 | 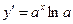 | 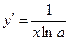 | 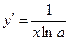 | |
| Интервалы возрастания функции | - | 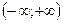 | - | 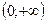 | - |
| Интервалы убывания функции | - | - | 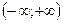 | - | 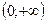 |
| Точки максимума функции | - | - | - | - | - |
| Максимумы функции | - | - | - | - | - |
| Точки минимума функции | - | - | - | - | - |
| Минимумы функции | - | - | - | - | - |
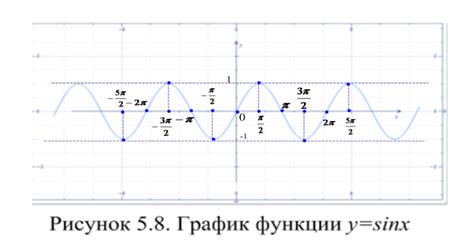
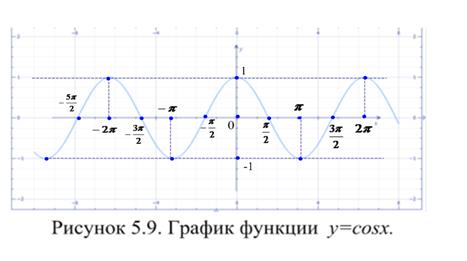
Свойства основных тригонометрических функций отражены в таблице 5.3, а их графики на рисунках 5.8 – 5.11. Функция 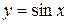 сопоставляет каждому действительному числу его синус; функция
сопоставляет каждому действительному числу его синус; функция 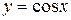 сопоставляет каждому действительному числу его косинус.
сопоставляет каждому действительному числу его косинус.
Числовые функции 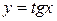 и
и 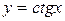 называют соответственно тангенсом и котангенсом. Так функция
называют соответственно тангенсом и котангенсом. Так функция 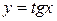 каждому действительному числу
каждому действительному числу 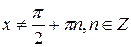 ставит в соответствие его тангенс, а функция
ставит в соответствие его тангенс, а функция 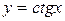 каждому действительному числу
каждому действительному числу 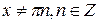 ставит в соответствие его котангенс.
ставит в соответствие его котангенс.
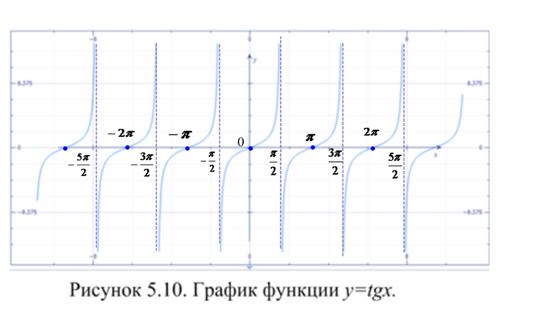
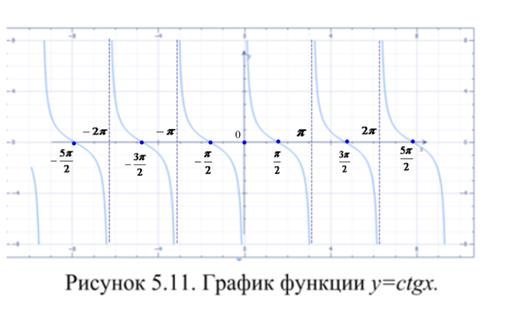
Заметим, что из всех основных элементарных функций, только тригонометрические функции являются периодическими. Наименьший положительный период для функций 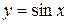 и
и 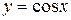 равен
равен 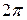 , а для функций
, а для функций 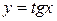 и
и 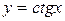 равен
равен 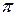 . Отметим, что функции
. Отметим, что функции 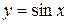 ,
, 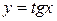 и
и 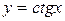 являются нечётными, а функция
являются нечётными, а функция 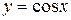 - чётной.
- чётной.
Таблица 5.3. Тригонометрические функции
| Функция | 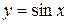 | 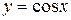 | 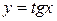 | 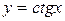 |
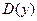 | R | R | 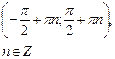 | 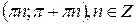 |
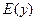 | 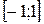 | 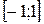 | R | R |
Точки пересечения с осью 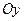 | 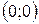 | 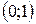 | 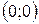 | - |
Точки пересечения с осью 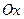 (нули функции) (нули функции) | 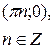 | 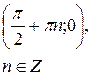 | 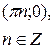 | 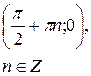 |
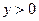 при при 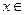 | 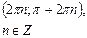 | 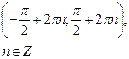 | 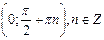 | 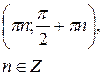 |
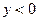 при при 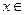 | 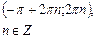 | 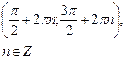 | 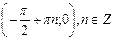 | 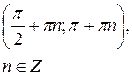 |
| Производная функции | 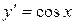 | 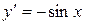 | 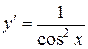 | 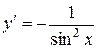 |
| Интервалы возрастания функции | 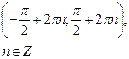 | 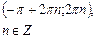 | 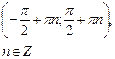 | - |
| Интервалы убывания функции | 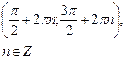 | 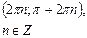 | - | 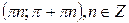 |
| Точки максимума функции | 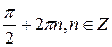 | 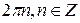 | - | - |
| Максимумы функции | - | - | ||
| Точки минимума функции | 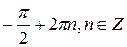 | 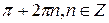 | - | - |
| Минимумы функции | -1 | -1 | - | - |
Перейдём к определению обратных тригонометрических функций. Заметим, что обратная тригонометрическая функция может быть построена только на участке монотонности тригонометрической функции.
По определению,
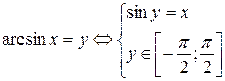 ;
; 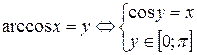 ;
;
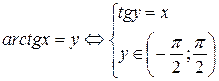 ;
; 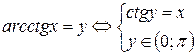 .
.
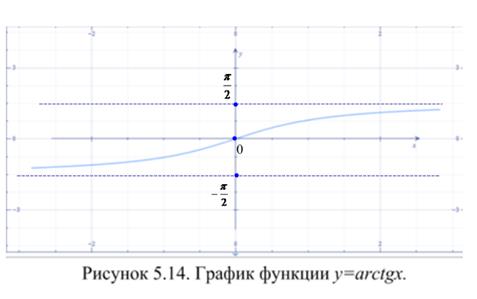
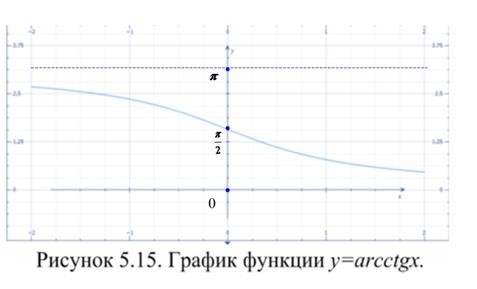
Свойства этих функций отражены в таблице 5.4, а их графики представлены на рисунках 5.12 – 5.15.
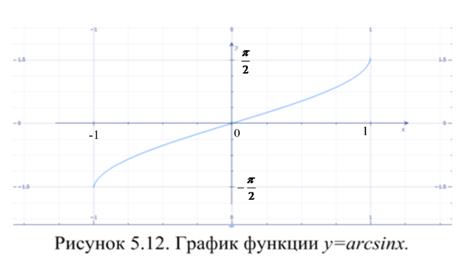
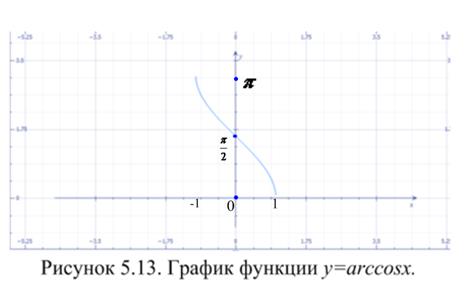
Таблица 5.4. Обратные тригонометрические функции
| Функция | 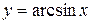 | 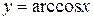 | 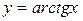 | 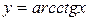 |
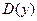 | 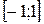 | 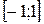 | R | R |
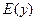 | 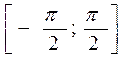 | 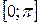 | 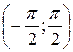 | 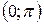 |
Точки пересечения с осью 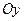 | 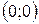 | 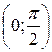 | 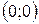 | 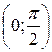 |
Точки пересечения с осью 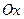 (нули функции) (нули функции) | 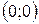 | 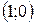 | 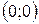 | - |
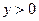 при при 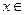 | 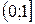 | 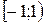 | 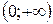 | R |
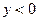 при при 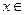 | 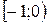 | - | 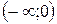 | - |
| Производная функции | 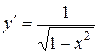 | 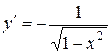 | 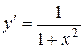 | 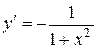 |
| Интервалы возрастания функции | 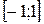 | - | R | - |
| Интервалы убывания функции | - | 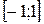 | - | R |
| Точки максимума функции | - | - | - | - |
| Максимумы функции | - | - | - | - |
| Точки минимума функции | - | - | - | - |
| Минимумы функции | - | - | - | - |
| Чётность | нечётная | ни чётная, ни нечётная | нечётная | ни чётная, ни нечётная |
Всякая функция, которая получается из основных элементарных функций путем конечного числа суперпозиций и четырех арифметических действий (сложения, вычитания, умножения и деления), называется элементарной функцией.
5.5
Пусть на плоскости помимо «старой» системы координат 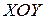 дана «новая» система координат
дана «новая» система координат 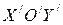 . Требуется установить связь между старыми координатами и новыми. Пусть
. Требуется установить связь между старыми координатами и новыми. Пусть 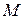 – произвольная точка плоскости,
– произвольная точка плоскости, 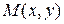 в
в 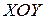 и
и 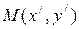 в
в 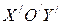 . Рассмотрим три случая.
. Рассмотрим три случая.
I.Пусть новые оси координат получаются в результате параллельного переноса старых, причем 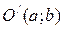 в
в 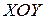 (Рисунок 5.16).
(Рисунок 5.16).
Тогда 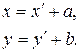
Формулы обратного перехода: 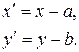
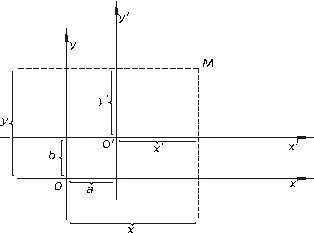
Рисунок 5.16. Параллельный перенос.
II. Пусть новые оси получаются в результате зеркального отражения старых, например, относительно оси 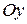 (Рисунок 5.17).
(Рисунок 5.17).
Тогда 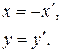
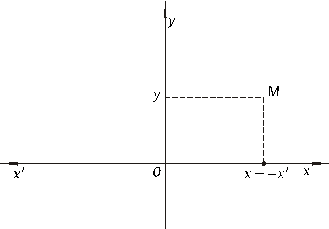
Рисунок 5.17. Зеркальное отображение.
III. Пусть новые оси получаются в результате поворота старых вокруг начала координат на угол 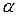 (Рисунок 5.18). Тогда из равенств
(Рисунок 5.18). Тогда из равенств
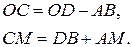
Получаем 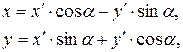
тогда формулы обратного перехода 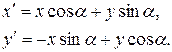
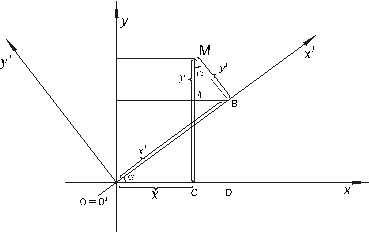
Рисунок 5.18. Поворот.
Замечание. Общий случай перехода от одной декартовой системы координат к другой сводится к комбинации разнообразных частных случаев.
5.6
Часто график одной функции можно получить из графика другой с помощью геометрических преобразований. Рассмотрим основные из них.
