Тема 2.1. Понятия о функции одной переменной. Предел и непрерывность функции

ПустьD— некоторое множество чисел. Если задан закон, по которому каждому числуxиз множестваDставится в соответствие единственное определенное числоy, то будем говорить, что на множествеDзадана функция, которую назовёмf. Числоy— это значение функцииfв точкеx, что обозначается формулойy = f(x).

Число x называется аргументом функции, множество D — областью определения функции, а все значения y образуют множество E, которое называется множеством значений или областью изменения функции.

Функцияf называется возрастающей (убывающей) на множествеG, если для любых чиселх₁ и х₂ из множества G, таких что x₁ < x₂, выполняется условие f(x₁) < f(x₂) (f(x₁) > f(x₂)).

Так как между множеством действительных чисел и множеством точек числовой оси можно установить взаимно-однозначное соответствие, в дальнейшем изложении понятиям “число х”и “точка х числовой оси” в некоторых случаях будет придаваться один и тот же смысл. Например, вместо “значение функции при значении аргумента, равном х₁” будет говориться “значение функции в точке х₁”. В нижеследующем опре­делении можно везде заменить выражение “точка х” на выражение “число х”.

Пусть e — некоторое положительное число, тогда eназывается окрестностью точки x₀ множества всех точек x, принадлежащих промежутку (x₀ ‑ e, x₀ + e), кроме самой точки x₀. Принадлежность точки x e‑окрестности точки 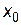можно выразить с помощью двойного неравенства

0 < êx – x₀ç < e.

Рассмотрим предел и непрерывность функции y = x² в точке x₀ = 2. Значение функции в этой точке равно 4.

Отметим одну особенность поведения функции в этой точке. Можно

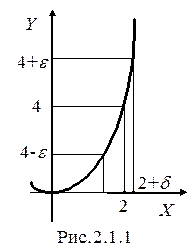выбрать какое-либо поло­жительное число eи построить e-окрестность точки y₀ = 4. Очевидно, что найдется такая окрестность точки x₀ = 2 (на рисунке 2.1.1 эта окрестность имеет радиус d) , что если x будет лежать в этой окрестности, то соответствующее значение y, равное x², попадет в e-окрестность точки y₀ = 4. Это заключение справедливо для любого, сколь угодно малого числа e. Здесь точка x₀ = 2 выбрана произвольно. Можно было бы для данной функции выбрать любую другую точку и сделать подобное заключение.

Рассмотрим функцию 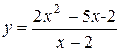.Эта функция не определена в точке x₀ = 2. При x₀ ¹ 2 её можно преобразовать:

.

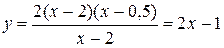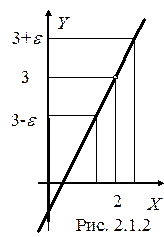
График функции представлен на рисунке 2.1.2. Хотя исходная функция не определена в точке x₀ = 2 и естественно не равна 3 в этой точке, точка y₀ = 3 имеет характерную особенность. Выбрав положитель­ное число e, можно утверждать, что если рассматривать значения x, расположенные достаточно близко к точке x₀ = 2 (или лежащие в некоторой окрестности точки x₀ = 2, причем радиус этой окрестности зависит от e), то соответствующие значения y попадут в e-окрестность точки y₀ = 3. Всё сказанное остаётся справедливым независимо от того, насколько малым выбрано положительное число e.

Введем понятие предела функции. Число A называется пределом функции y = f(x) в точке x₀ (иногда говорят, при x, стремящемся к x₀), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d-окрестности точки x₀ соответствующие значения y попадают в e-окрестность точки y = A.

Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f(x) в точке x₀, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию

0 < êx – x₀ê < d,

выполняется условие

êy – Aê < e.

Тот факт, что A есть предел функции y = f(x) в точке x = x₀, записывается формулой:

.

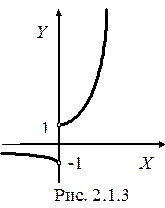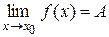Как видно из второго из рассмотренных выше примеров, для того, чтобы функция имела предел в точке x = x₀, не требуется, чтобы она была определена в этой точке.

Рассмотрим функцию 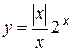. Очевидно, что если x > 0, то y = 2^x; если x < 0, то y = –2^x; при x = 0 функция не определена.

График функции изображен на рисунке 2.1.3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.

Функция y = f(x) называется непрерывной в точке x = x₀, если она определена в этой точке и ее значение f(x₀) равно пределу функции в этой точке: .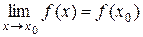

Функция y = x² непрерывна в точке x = 2, как и во всех точках числовой оси. Функция 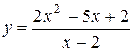не является непрерывной в точке x = 2. Функция 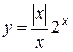не является непрерывной в точке x = 0.

Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.