Погрешности результатов элементарных арифметических операций

Рассмотрим простейшие арифметические операции.

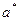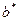1. При сложении приближенных величин их абсолютные погрешности складываются. Действительно, пусть и - приближенные значения величин 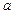и 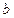, полученные с абсолютными погрешностям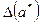и и 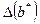соответственно, т.е.

,

.

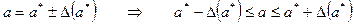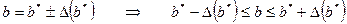Сложим почленно двойные неравенства, определяющие границы значений для 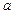и :

.

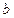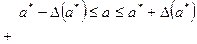
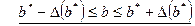
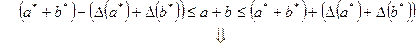
Относительная погрешность суммы будет заключена между наибольшей и наименьшей относительными погрешностями слагаемых.

2. При вычитании приближенных величин абсолютная погрешность разности будет равна сумме абсолютных погрешностей уменьшаемого и вычитаемого.

Задание. Доказать истинность предыдущего утверждения.

Относительная погрешность разности приближенных величин будет больше каждой из относительных погрешностей уменьшаемого и вычитаемого.

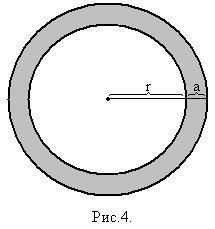Если уменьшаемое значительно больше вычитаемого, то относительную погрешность разности можно оценить также, как при сложении, если же уменьшаемое и вычитаемое близки друг к другу, то при вычитании происходит большая потеря верных знаков и рост погрешности. Поэтому там, где это возможно, надо стараться избегать вычитания близких по абсолютной величине чисел. Это иногда удается достичь некоторым преобразованием формулы. Пусть, например, необходимо вычислить площадь, заключенную между двумя окружностями с общим центром, если дан радиус меньшей окружности 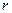, а разность радиусов равна 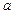(рис.4). Искомая площадь будет определяться формулой:

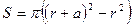, (4)

и если 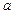- мало, т.е. 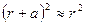, то при вычислении по формуле (4) будет иметь место вычитание близких чисел. Во избежание этого воспользуемся известной формулой квадрата суммы:

,

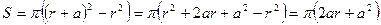которая позволяет после преобразования уйти от вычитания близких чисел.

Задание. Привести примеры задач, при решении которых присутствует вычитание близких чисел. Преобразовать расчетную формулу так, чтобы вычитание близких чисел ушло.

3. При умножении и делении приближенных величин относительные погрешности складываются.

Вопросы

1. Насколько актуальной в настоящее время является разработка новых и совершенствование уже имеющихся численных методов решения задач? Почему?

2. Чем вызвано резкое расширение приложений математики в настоящее время?

3. В чем состоит математизация нематематических областей: химии, экономики, биологии, геологии и т.д.?

4. Какие существенные факторы обусловили достижения в области использования ЭВМ?

5. Что можно сказать об эффекте, который достигается за счет совершенствования численных методов решения сложных прикладных задач по сравнению с эффектом, достигаемым за счет повышения производительности ЭВМ? Обосновать.

6. Чем можно объяснить быстрое проникновение математики во все области человеческого знания?

7. Чем в основном определяется развитие как теоретических, так и прикладных разделов математики и других областей науки?

8. В чем заключается особенность и значимость прикладных исследований для общества?

9. Какие аспекты важны для работы в области приложений математики? Пояснить.

10. Какая область математики называется вычислительной математикой?

11. Какой метод является основным в вычислительной математике?

12. В чем состоят источники погрешности численного решения задачи?

13. Какие виды погрешностей существуют? Привести примеры.

14. Абсолютная и относительная погрешности – определения, примеры вычислений. Какая из этих погрешностей отражает качество полученного приближения. Значащие и верные цифры в записи числа. Примеры.

15. Как погрешности результатов элементарных арифметических операций связаны с погрешностями операндов?

16. Почему надо избегать вычитания близких чисел? Всегда ли это можно сделать?

17. Что происходит с вычислительной погрешностью с ростом количества операций?

Литература

1. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с.
2. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с.
3. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
4. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения) / Н.С.Бахвалов — М.: Наука. Гл.ред.физ.-мат.лит. ,1975. — 632 с.
5. Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с.
6. Парлетт Б. Симметричная проблема собственных значений. Численные методы / Парлетт Б.; пер. с англ. Х.Д.Икрамова и Ю.А.Кузнецова. — М.: Мир, 1983. — 384с.
7. Гантмахер Ф.Р. Теория матриц / Ф.Р.Гантмахер. — М.: Наука, 1988. — 552 с.
8. Ланкастер П. Теория матриц / П.Ланкастер; пер.с англ. С.П.Демушкина. — М.: Наука, Гл.ред.физ.-мат.лит.,1978. — 280 с.
9. Хорн Р. Матричный анализ / Р.Хорн, Ч.Джонсон. — М.: Мир,1989. — 655 с.
10. Воеводин В.В. Матрицы и вычисления / В.В.Воеводин, Ю.А.Кузнецов. — М.: Наука,1984. — 365 с.
11. Икрамов Х.Д. Численные методы для симметричных линейных систем / Х.Д.Икрамов. — М.: Наука, 1988. — 289 с.
12. Джордж А. Численное решение больших разреженных систем уравнений / А.Джордж, Дж.Лю; пер. с англ. Х.Д.Икрамова. — М., Мир, 1984. — 333 с.