Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Рассмотрим важный и весьма распространенный случай, когда в уравнении вида

.

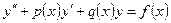(8.6.1)

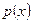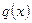где и – постоянные величины.

Определение

Уравнения такого вида называются линейными дифференциальным уравнением второго порядка с постоянными коэффициентами.

Как и в общем случае линейных дифференциальных уравнений второго порядка, основой в построении решения являются однородные уравнения.

Рассмотрим линейное однородное уравнение

,

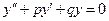(8.6.2)

где 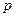и 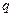– вещественные числа. Будем искать решение этого уравнения в ви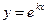де , где 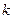– некоторое число. Подставляем эту функцию в уравнение (8.6.2): .

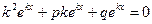Сокращая обе части уравнения на 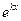получаем квадратное уравнение:

.

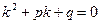(8.6.3)

Таким образом, если число k является корнем уравнения (8.6.3), то функция 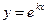есть решение однородного уравнения (8.6.2). Уравнение (8.6.3) называется характеристическим уравнением для уравнения (8.6.2).

Теорема: Если корни характеристического уравнения (8.6.3) вещественные и 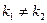, то общее решение однородного уравнения (8.6.2) имеет вид

.

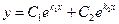(8.6.4)

Если корни характеристического уравнения (8.6.3) вещественные и равные 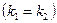, то общее решение однородного уравнения (8.6.2) имеет вид

.

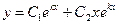(8.6.5)

Если корни характеристического уравнения (8.6.3) комплексные 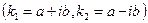, то общее решение однородного уравнения (8.6.2) имеет вид

,

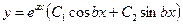(8.6.6)

где , .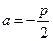

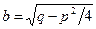Во всех трех случаях 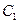и 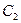– произвольные постоянные.

Заметим, что в последнем случае корни характеристического многочлена с действительными коэффициентами представляют собой комплексно–сопряженные числа в алгебраической форме.

Пример

Решить задачу Коши , , .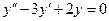

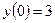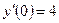Решение

Решение ищем в виде 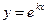. Подставляя решение в уравнение, находим характеристическое уравнение 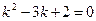. Его корни: 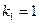, 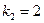. Тогда общее решение данного уравнения имеет вид: 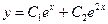. Найдем такие значения постоянных 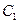и 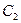, при которых выполняются заданные начальные условия. Так как 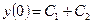, , 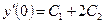то постоянные 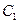и 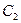находим, решая систему:

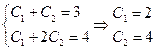. Частное решение уравнения имеет вид .

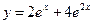Пример

Решить задачу Коши , , .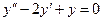

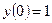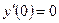Решение

Решение ищем в виде 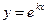. Подставляя решение в уравнение, находим характеристическое уравнение 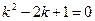. Его корни: 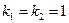. Тогда общее решение данного уравнения имеет вид: 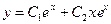. Найдем такие значения постоянных 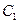и 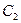, при которых выполняются заданные начальные условия. Так как 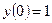, т.е. 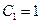; 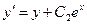, то 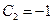. Таким образом, частное решение имеет вид .

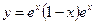Перейдем теперь к решению линейного неоднородного уравнения с постоянными коэффициентами.

Это уравнение может быть в частности решено методом вариации постоянных, который состоит в следующем. Сначала находится общее решение однородного уравнения 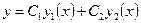. Затем предполагается, что постоянные 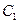и 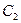являются функциями независимой переменной 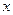. При этом функци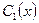и и 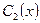могут быть найдены как решения системы:

.

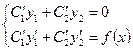(8.6.7)

Пример

Решить уравнение .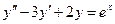

Решение

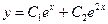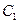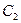Решение однородного уравнения есть функция . Полагая теперь, что и являются функциями независимой переменной 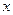, найдем первые производные этих функций, решая систему: .

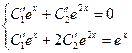Найдем 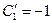, 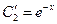. Полученные дифференциальные уравнения – с разделяющимися переменными. Решая эти уравнения, получаем: 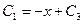, . Таким образом, окончательное решение уравнения имеет вид: .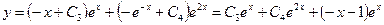

Обратим внимание на структуру полученного решения. Первые два слагаемых – это общее решение однородного уравнения, последнее – частное решение неоднородного уравнения.