Непрерывное вероятностное пространство
Как уже говорилось ранее, множество элементарных исходов может быть более, чем счетным (то есть несчетным). Так несчётное множество исходов имеет эксперимент, состоящий в случайном бросании точки на отрезок [a1; a2]. Можно себе представить, что эксперимент, заключающийся в измерении температуры в заданный момент в заданной точке тоже имеет несчётное число исходов (действительно, температура может принять любое значение из некоторого промежутка, хотя в действительности мы можем измерять её лишь с определённой точностью, и практическая реализация такого эксперимента даст конечное число исходов). В случае эксперимента с несч ётным множеством элементарных исходов нельзя считать любое подмножество множества событием. Следует заметить, что подмножества , не являющиеся событиями, являются математическими абстракциями и не встречаются в практических задачах. Поэтому в нашем курсе данный параграф является необязательным.
Чтобы ввести определение случайного события, рассмотрим систему (конечную или счетную) подмножеств 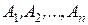 пространства элементарных исходов .
пространства элементарных исходов .
В случае выполнения двух условий:
1) из принадлежности А этой системе следует принадлежность 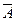 этой системе;
этой системе;
2) из принадлежности 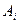 и
и 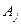 этой системе следует принадлежность Ai
этой системе следует принадлежность Ai 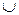 Aj этой системе
Aj этой системе
такая система подмножеств называется алгеброй.
Пусть — некоторое пространство элементарных исходов. Убедитесь в том, что две системы подмножеств:
1) , ; 2) , А, 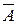 , (здесь А— подмножество W) являются алгебрами.
, (здесь А— подмножество W) являются алгебрами.
Пусть A1 и A2 принадлежат некоторой алгебре. Докажите, что A1 \ A2 и 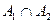 принадлежат этой алгебре.
принадлежат этой алгебре.
Назовём s-алгебройсистему Á подмножеств множества , удовлетворяющую условию 1) и условию 2)¢:
2) если подмножества А1, А2,¼, Аn, ¼принадлежат Á, то их счётное объединение 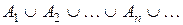 (по аналогии с суммированием это счётное объединение кратко записывается формулой
(по аналогии с суммированием это счётное объединение кратко записывается формулой 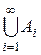 ) тоже принадлежит Á.
) тоже принадлежит Á.
Подмножество А множества элементарных исходов является событием, если оно принадлежит некоторой s-алгебре.
Можно доказать, что если выбрать любую счётную систему событий, принадлежащих некоторой s-алгебре и проводить с этими событиями любые принятые в теории множеств операции (объединение, пересечение, взятие разности и дополнения), то результатом будет множество или событие, принадлежащее той же s-алгебре.
Сформулируем аксиому, называемую аксиомой А.Н. Колмогорова.
Каждому событию соответствует неотрицательное и не превосходящее единицы числоP(А), называемое вероятностью событияА, причем функцияP(А) обладает следующими свойствами:
1)Р()=1
2) если событияA1, A2,..., An, ¼ несовместны, то
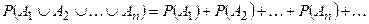 =
= 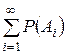
Если задано пространство элементарных исходов , алгебра событий и определенная на ней функция Р, удовлетворяющая условиям приведенной аксиомы, то говорят, что задано вероятностное пространство.
Это определение вероятностного пространства можно перенести на случай конечного пространства элементарных исходов . Тогда в качестве алгебры можно взять систему всех подмножеств множества .
