Классификация точек разрыва
Необходимое и достаточное условие непрерывности функции в точке
Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
| lim Δy = 0. |
| Δx → 0 |
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел
|
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
|
Непрерывность суммы, произведения и частного двух непрерывных функций
Теорема 1. Если функции f(x) и g(x) непрерывны в точке х0, то в этой точке непрерывны
f(x) ± g(x), f(x) · g(x),
(g(x0) ≠ 0). |
Непрерывность сложной функции
Теорема 2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.
Все элементарные функции непрерывны в каждой точке их областей определения.
Локальные свойства непрерывных функций
Теорема 3(ограниченность непрерывной функции). Если функция f(x) непрерывна в точке x0, то существует окрестность O(x0), в которой f(x)ограничена.
Доказательство следует из утверждения об ограниченности функции, имеющей предел.
Теорема 4 (устойчивость знака непрерывной функции). Если функция f(x) непрерывна в точке x0 и f(x0) ≠ 0, то существует окрестность точки x0, в которой f(x) ≠ 0, причем знак f(x) в этой окрестности совпадает со знаком f(x0).
Классификация точек разрыва
Условие (1) непрерывности функции f(x) в точке x0 равносильно условию
| f(x0 − 0) = f(x0 + 0) = f(x0), | (3) |
где f(x 0 − 0) = lim x → x0 − 0 f(x) и f(x0 + 0) = lim x → x0 + 0
f(x) — односторонние пределы функции f(x) в точке x0.
При нарушении условия (3) точка x0 называется точкой разрыва функции f(x). В зависимости от вида нарушения условия (3) точки разрыва имеют различный характер и классифицируются следующим образом:
1. Если в точке x0 существуют односторонние пределы f(x0 − 0), f (x0 + 0) и
| f(x0 − 0) = f(x0 + 0) ≠ f(x0), |
то точка х0 называется точкой устранимого разрыва функции f(x) (рис. 1).

 Замечание. В точке x0 функция может быть не определена.
Замечание. В точке x0 функция может быть не определена.
2. Если в точке x0 существуют односторонние пределы f(x0 − 0), f (x0 + 0) и
| f(x0 − 0) ≠ f(x0 + 0), |
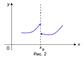
то точка x0 называется точкой разрыва с конечным скачком функции f(x) (рис.2).
Замечание. В точке разрыва с конечным скачком значение функции может быть любым, а может быть и не определено.
Точки устранимого разрыва и конечного скачка называются точками разрыва 1–го рода. Их отличительным признаком является существование конечных односторонних пределов f(x0 − 0) и
f(x0 + 0).
3. Если в точке x0 хотя бы один из односторонних пределов f(x0 − 0), f (x0 + 0) равен бесконечности или не существует, то x0 называется точкой разрыва 2–го рода (рис. 3).
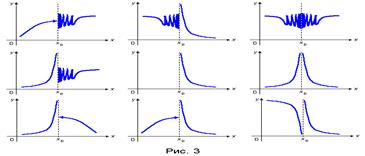
Если хотя бы один из односторонних пределов f(x0 − 0), f (x0 + 0) равен бесконечности, то прямая x = x 0 называется вертикальной асимптотой графика функции y = f(x).
17.
Арифметические операции над непрерывными функциями.
Теорема о переходе к пределу под знаком непрерывной функции.
Непрерывность суперпозиции функций.
Теор. о непрерывности суммы, произведения, частного. Пусть функции f(x), g(x) непрерывны в точке х0. Тогда в этой точке непрерывны функции f(x)±.g(x), f(x)g(x), 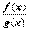 (частное - в случае, когда g(х0)¹0). Для примера докажем непрерывность частного. Пусть f(x), g(x) непрерывны в точке х0, т.е.
(частное - в случае, когда g(х0)¹0). Для примера докажем непрерывность частного. Пусть f(x), g(x) непрерывны в точке х0, т.е. 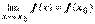 ,
, 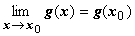 , причём g(х0)¹0. По теор. существует
, причём g(х0)¹0. По теор. существует 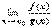 , и этот предел равен
, и этот предел равен 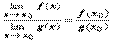 , что означает непрерывность функции
, что означает непрерывность функции 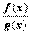 в точке х0. Теор. о переходе к пределу под знаком непрерывной функции. Пусть функция
в точке х0. Теор. о переходе к пределу под знаком непрерывной функции. Пусть функция 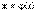 определена в некоторой окрестности точки t0 и имеет
определена в некоторой окрестности точки t0 и имеет 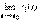 , равный х0. Пусть точка
, равный х0. Пусть точка 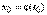 принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда существует
принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда существует 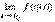 , и
, и 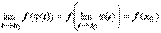 .
.
Док-во. Возьмём "e>0. Так как f(x) непрерывна в точке х0, то $s>0, такое что | х- х0|<sÞ Þ | f(x)- f(x0)|<e. Так как существует 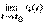 = х0, то для s d>0, такое что 0<| t- t0|<d Þ
= х0, то для s d>0, такое что 0<| t- t0|<d Þ
Þ |j (t)- х0|<s. Таким образом, для "e>0 мы нашли такое d>0, что из 0<| t- t0|<dÞ
Þ | f(x)- f(x0)|= | f(j (t))- f( 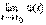 )|<e, что означает существование предела
)|<e, что означает существование предела 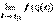 и равенство этого предела величине
и равенство этого предела величине 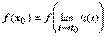 .
.
Теор. о непрерывности суперпозиции непрерывных функций. Пусть функция 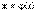 непрерывна в точке точке t0. Пусть точка
непрерывна в точке точке t0. Пусть точка 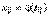 принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда сложная функция
принадлежит области определения функции y = f(x), и f(x) непрерывна в точке х0. Тогда сложная функция 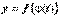 непрерывна в точке t0.
непрерывна в точке t0.
Док-во непосредственно следует из предыдущей теоремы. Так как j (t) непрерывна в точке t0, то 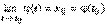 . Поэтому
. Поэтому 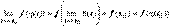 , что и означает непрерывность сложной функции
, что и означает непрерывность сложной функции 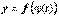 в точке t0.
в точке t0.
Односторонние пределы
Пусть переменная x стремится к a, оставаясь больше a, и при этом 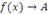 . Тогда число A называют правосторонним пределом (или пределом справа) функции
. Тогда число A называют правосторонним пределом (или пределом справа) функции 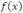 и обозначают любым из символических выражений
и обозначают любым из символических выражений 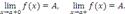
Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае 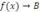 при x → a со стороны меньших значений:
при x → a со стороны меньших значений: 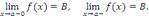
Для существования обычного (двустороннего) предела функции 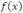 в точке a необходимо и достаточно равенство между собой односторонних пределов:
в точке a необходимо и достаточно равенство между собой односторонних пределов: 
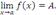
Например, в точке x = 3 односторонние пределы функции 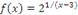 отличаются друг от друга:
отличаются друг от друга:
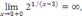
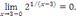
Поэтому в рассматриваемой точке предел функции 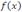 не существует.
не существует.
Точки разрыва функции
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
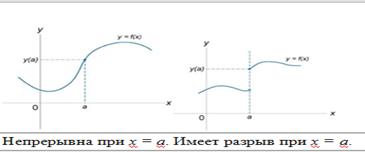
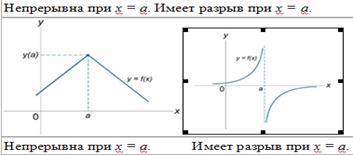
Наши рекомендации
