Логарифмическое дифференцирование
Рассмотрим функцию 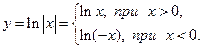 .
.
Тогда 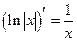 , т.к.
, т.к. 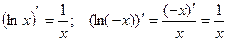 .
.
Учитывая полученный результат, можно записать 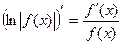 .
.
Отношение 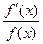 называется логарифмической производной функции
называется логарифмической производной функции  .
.
Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
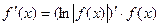
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Производная показательно- степенной функции
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть 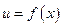 и
и 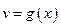 – функции, имеющие производные в точке
– функции, имеющие производные в точке  ,
, 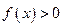 .
.
Найдем производную функции 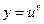 . Логарифмируя, получим:
. Логарифмируя, получим:
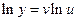 ,
,
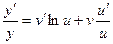 ,
,
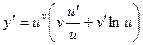 ,
,
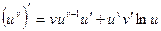 .
.
Пример. Найти производную функции 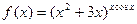 .
.
По полученной выше формуле получаем: 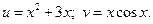
Производные этих функций: 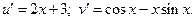
Окончательно:
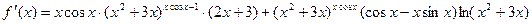 .
.
Производная обратной функции
Пусть требуется найти производную функции 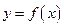 при условии, что обратная ей функция
при условии, что обратная ей функция 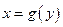 имеет производную, отличную от нуля в соответствующей точке
имеет производную, отличную от нуля в соответствующей точке 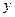 .
.
Для решения этой задачи дифференцируем функцию 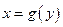 по
по  :
:
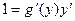 .
.
Так как 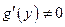 , то
, то
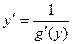 ,
,
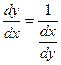 ,
,
т.е. производная обратной функции равна обратному значению данной функции.
Пример. Найти формулу для производной функции 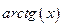 .
.
Функция 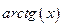 является функцией, обратной функции
является функцией, обратной функции 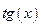 , т.е. ее производная может быть найдена следующим образом:
, т.е. ее производная может быть найдена следующим образом:
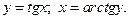
Известно, что 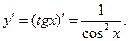 Используя приведенную выше формулу получаем:
Используя приведенную выше формулу получаем:
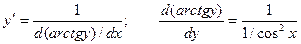 .
.
Т.к. 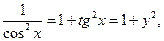 то можно записать окончательную формулу для производной арктангенса:
то можно записать окончательную формулу для производной арктангенса:
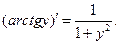
Аналогично получаются другие формулы для производных арксинуса, арккосинуса и других обратных функций, приведенные в таблице производных.
Дифференциал функции. Геометрический смысл дифференциала
Пусть функция 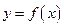 имеет производную в точке
имеет производную в точке  :
:
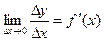
Тогда справедливо равенство: 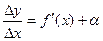 , где
, где 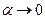 , при
, при 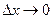 .
.
Следовательно: 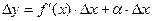 .
.
Величина 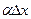 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 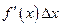 , т.е.
, т.е. 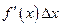 - главная часть приращения
- главная часть приращения 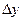 .
.
Определение. Дифференциалом функции  в точке
в точке  называется главная линейная часть приращения функции. Обозначается
называется главная линейная часть приращения функции. Обозначается 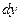 или
или 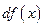 .
.
Из определения следует, что 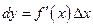 или
или 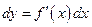 , так как
, так как 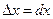 . Следовательно,
. Следовательно, 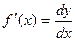 .
.
Геометрический смысл дифференциала.
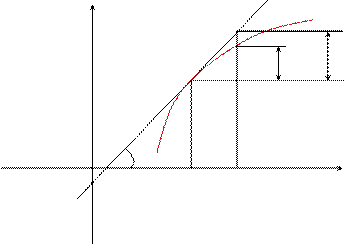 y
y

K
M 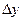
L
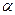
x 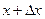 x
x
Из треугольника 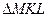 находим
находим 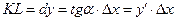 .
.
Таким образом, дифференциал функции  в точке
в точке  равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
