А) Найти вероятность наугад открыть камеру хранения
Б) Найти вероятность наугад открыть камеру хранения, если дополнительно стало известно, что все цифры на правильном номере разные.
Решение.
а) всего комбинаций из 10 цифр по 4 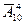 =104 вариантов. Открывает дверцу только одна из них, из чего вероятность наудачу открыть ее равна 1/10000 = 0,0001;
=104 вариантов. Открывает дверцу только одна из них, из чего вероятность наудачу открыть ее равна 1/10000 = 0,0001;
б) всего комбинаций из 10 цифр по 4, если все цифры различны –  =10×9×8×7=5 400 вариантов. Открывает дверцу по-прежнему только один, откуда вероятность открыть дверцу становится
=10×9×8×7=5 400 вариантов. Открывает дверцу по-прежнему только один, откуда вероятность открыть дверцу становится  .
.
Таким образом, вероятность в простейшем случае вычисляется комбинаторно.
Свойства вероятности
1. Из определения вероятности следует, что вероятность случайного события А не больше единицы и не меньше нуля. 0<=P(A)<=1.
2. Любое событие может либо произойти, либо не произойти. Это означает, что сумма вероятностей некоторого события А и события, ему противоположного, равна 1.Р(А)+Р(  )=1 (где
)=1 (где  – противоположное событие или условие по отношению к А).
– противоположное событие или условие по отношению к А).
Часто для вычисления вероятностей используют переход к противоположному событию Р(А)=1–Р(  ).
).
Задача. В некоторой детской игре для начала игры участнику нужно обязательно выбросить пятерку. Поскольку граней на косточке всего шесть, то кажется, что уж в шести бросках пятерка выпадет наверняка. Найдите вероятность этого события.
Решение. Р (хоть один раз из шести выпадет «5»)=1–Р(ни разу из шести не выпадет «5»)= 
3. Иногда разбивают сложный благоприятный исход на простейшие или стандартные.
Р(А или В)=Р(А)+Р(В)–Р(А и В) – вероятность того, что произойдет событие А или событие В, равна сумме вероятностей этих событий минус вероятность того, что события А и В произойдут одновременно.
Задача. Игральную кость подбрасывают один раз. Какова вероятность выпадения либо четного числа очков, либо числа, кратного трем?
Решение. Введем обозначения:
А – выпадения либо четного числа очков, либо числа, кратного трем;
В – выпадения четного числа очков;
С – выпадения числа, кратного трем.
Р(А)=Р(В или С)=Р(А)+Р(В)-Р(В и С)=3/6+2/6-1/6=2/3.
Задача. Игральную кость подбрасывают один раз. Найти вероятность, что выпадет число очков не менее пяти.
Решение. Р(выпадение числа очков не менее пяти)=Р(выпадение «5»)+
+Р(выпадение «6») = =1/6+1/6 =1/3.
Бином Ньютона
Правила и формулы комбинаторики часто используют при решении различных задач математики. Комбинаторные доказательства отличаются простотой и особой изысканностью. Рассмотрим применение комбинаторики к доказательству формулы бинома Ньютона.
Биномом Ньютона называют формулу для вычисления выражения (а+b)n для натуральных n.
Теорема. 
Доказательство.Данную формулу можно доказать методом математической индукции. Ниже представлено комбинаторное доказательство.
Запишем (a+b)n в виде произведения (a+b)n=(a+b) × (a+b) × …× (a+b).
Раскроем скобки в правой части этого равенства и запишем все слагаемые в виде произведения n сомножителей а и b в том порядке, в котором они появляются.
Например, (a+b)2 запишется в виде (a+b)2=(a+b)× (a+b)=aa+ab+ba+bb, а (a+b)3 – в виде (a+b)3=(a+b)×(a+b)×(a+b) =aaa+aab+aba+abb+baa+bab+bba+bbb.
Видно, что в обе формулы входят все размещения с повторениями, составленные из букв а и b по две (три) буквы в каждом.
В общем случае – после раскрытия скобок получим всевозможные размещения с повторениями букв а и b, состоящие из n элементов. Используя коммутативность, приведем подобные члены. Подобными будут члены, содержащие одинаковое количество букв а (тогда и букв b в них будет одинаковое количество). Членов, в которые входит k букв a и, следовательно, (n–k) букв b, ровно Р(k, n–k)= 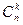 . Отсюда вытекает, что после приведения подобных членов выражение akbn-k войдет с коэффициентом
. Отсюда вытекает, что после приведения подобных членов выражение akbn-k войдет с коэффициентом 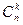 , поэтому формула примет вид:
, поэтому формула примет вид:  .
.
Задача. Раскрыть скобки и привести подобные члены в выражении (3х+2у)4, используя формулу бинома Ньютона.
Решение. 
Задача. Найти коэффициент при х2 в разложении (2х+3)6.
Решение. В данной задаче требуется найти коэффициент только при х2, поэтому нет необходимости раскрывать все выражение по формуле бинома Ньютона. Достаточно рассмотреть только одно слагаемое
 .
.
Таким образом, х2 в разложении (2х+3)6 будет иметь коэффициент 4 860.
Числа 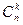 называют биномиальными коэффициентами.
называют биномиальными коэффициентами.
С помощью бинома Ньютона легко доказать свойства биномиальных коэффициентов (чисел 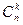 ).
).
