Показательная и логарифмическая функции, тригонометрические и обратные тригонометрические функции являются обратными

Область определения X функции f(x) является областью значений Y обратной функции g(y) и наоборот.

Неявная функция

Если зависимость между x и y выражена уравнением, не разрешенным относительно y, то говорят о неявной функции.

þ Обозначение: F(x, y) = 0.

! Пример: x² + e^x + y + lny = 0. Это уравнение не разрешается относительно y, поэтому функция является неявной.

Вышеприведенные элементарные функции – это явные функции.

Кусочно-линейная функция

При закупке товара, в случае больших партий товара, часто предоставляется оптовая скидка:

.

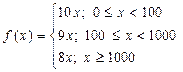Такая функция называется кусочно-линейной функцией.

Функции задаются тремя способами: аналитическим, табличным и графическим способами. График линейной функции называется прямой линией, график квадратичной функции – параболой, график обратной зависимости от x – гиперболой.

Функции нескольких переменных

Функция двух переменных

Величина z называется функцией двух переменных x, y, если каждой паре (x, y) чисел соответствует одно или несколько значений z.

þ Обозначение: z = f(x, y) («зет равно эф от икс, игрек»), (x, y) называются аргументами.

! Примеры: Спрос Q есть функция дохода R и цены p: Q = f(R, p); в термодинамике давление p есть функция температуры T и объема V (уравнение Менделеева-Клапейрона).

Множество M значений (x, y), для которого функция z определена, называется областью определения функции.

@ Задача 1. Найти область определения функции .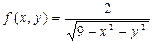

Решение: Функция f(x, y) имеет смысла при x² + y² < 9, т.е. областью определения функции является круг с радиусом 3 без точек окружности.

В трехмерном пространстве функции двух переменных соответствует поверхность.

! Примеры: 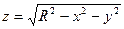- полусфера, z = x² + y² - параболоид.

Функция f(x, y)называется непрерывной в точке M₀(x₀, y₀), если соблюдаются следующие два условия:

1. в точке M₀ функция имеет определенное значение b,

2. в точке M₀ функция имеет предел, равный b .

Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в этой точке.

Функция f(x, y) называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.

Функция нескольких переменных

þ Обозначение: y = f(x₁, x₂¼, x_n).

! Примеры: Производственная функция Q = f(K, L, N) является функцией 3 переменных (факторов производства), где Q – выпуск, K - капитал, L - затраты на труд, N - природные ресурсы. Частным случаем является функция Кобба-Дугласа 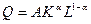, где A характеризует эффективность применяемой технологии, a – коэффициент эластичности по капиталовложению.

§3.3. Производная функции

Производная функции

Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a, b), и пусть x – какая-то точка этого промежутка. Дадим аргументу приращение Dx, тогда функция получит приращение, равное Dy = f(x + Dx) – f(x). Если функция непрерывная и приращение аргумента бесконечно малая величина, то приращение функции тоже бесконечно малая величина.

Предел, к которому стремится отношение 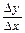при Dx® 0, называется производной функции:

.

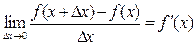þ Обозначение: f¢(x) («эф штрих икс»), y¢ («игрек штрих»)

! Примеры производных линейной функции y = x и квадратичной функции y = x².

.

.

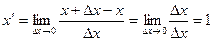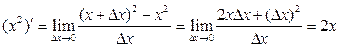Производная степенной функции равна произведению степени на степенную функцию, у которой показатель на единицу меньше:

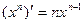. (1)

Производные функций y = x, y = x² являются частными случаями формулы (1), при n = 1; 2. Производные 1¢ = 0, 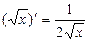, , 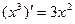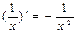тоже являются частными случаями формулы (1), при n = 0; ½; 3; – 1.

! Пример: Производная тригонометрической функции y = sinx равна

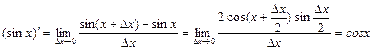. (2)

Таким же образом находится производная функции cosx:

(cosx)¢ = – sinx. (3)

! Пример: Производная экспоненциальной функции y = e^x равна

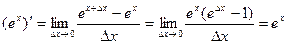. (4)

Свойства производной

1. Постоянный множитель можно вынести за знак производной: (cf(x))¢ = cf¢(x).

2. Производная суммы равна сумме производных:

(f(x) ± g(x))¢ = f¢(x) ± g¢(x).

3. Производная произведения равна

(f(x)g(x))¢ = f¢(x)g(x) + f(x)g¢(x).

4. Производная отношения равна

.

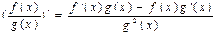! Пример: Производная тригонометрической функции y = tgx равна

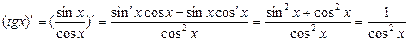. (5)

Таким же образом находится производная функции сtgx:

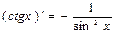. (6)

@ Задача 1. Найти производную постоянной функции y = c.

Решение: Производную находим с помощью 1 свойства производной и формулы (1):

c¢ = c·1¢ = c·0 = 0.

@ Задача 2. Найти производную функции

f(x) = (2x³ – 3x + 1)cosx и вычислить f¢(0).

Решение: При нахождении производной заданной функции применяются свойства производных и производные степенных и тригонометрических функций:

f¢(x) = (2x³ – 3x + 1)¢cosx + (2x³ – 3x + 1)(cosx)¢ =

= (6x² – 3)cosx – (2x³ – 3x + 1)sinx; f¢(0) = – 3.

Процедура нахождения производной называется дифференцированием.