Обратные тригонометрические функции

По определению W=arccos(z), если cosW=z. Из этого следует, что

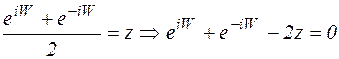(1)

Умножим (1) на 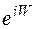, имеем: 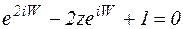(2)

Решая квадратное уравнение (2) найдем:

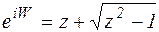(корень алгебраический)

,

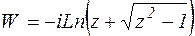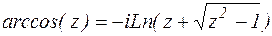
Аналогично можно показать, что .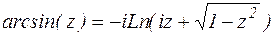

ЛЕКЦИЯ 4

План лекции

1. Понятие контурного интеграла функции комплексного переменного.

2. Связь контурного интеграла с криволинейными интегралами функций вещественного переменного.

3. Свойства интегралов.

4. Теорема о независимости значения интеграла от пути интегрирования.

ПОНЯТИЕ КОНТУРНОГО ИНТЕГРАЛА ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

Пусть на некоторой плоскости z задан некоторый контур С, точками 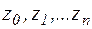. Разобьем его на n (частей) дуг. На дуге 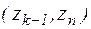произвольно выберем точку .

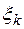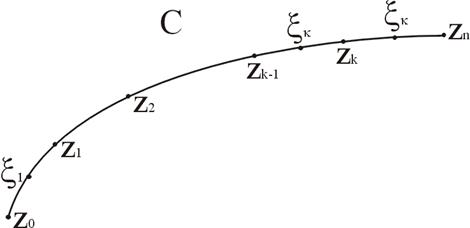Рис. 1

Составим интегральную сумму: 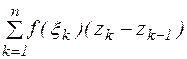. Обозначим .

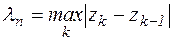Контурным интегралом функции комплексного 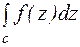переменного называется 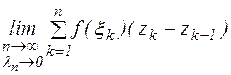, если существует, не зависит от способа деления контура С точками 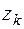и от выбора точек 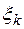на дуге .

=

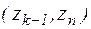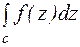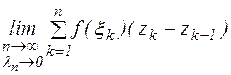
Теорема 2. Если С кусочно - гладкая линия, а f(z) кусочно – непрерывна и ограничена на контуре С , то 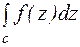существует.

Доказательство: Положим , , .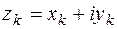

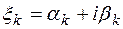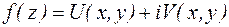Выпишем интегральную сумму: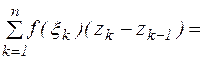

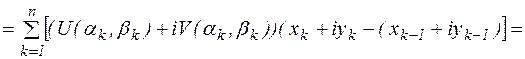
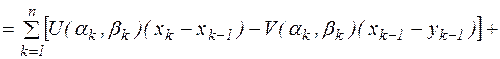
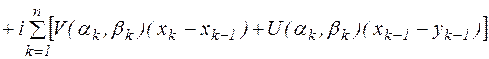(1)

Перейдем в (1) к пределу при 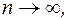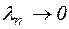. Тогда интегральные в правой части (1) по определению являются криволинейными интегралами II рода. При условиях сформулированных в теореме 2 эти интегралы существуют.

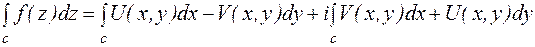(2)

Так как контурный интеграл комплексного переменного сводится к двум криволинейным интегралам функции вещественного переменного, то на него распространяются свойства характерных для криволинейных интегралов.

,

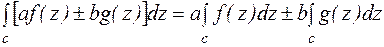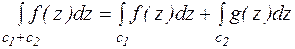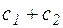, ( - контур из контуров 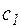и )

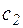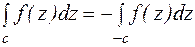(-с – контур с, проходимый в противоположном направлении)

Рассмотрим 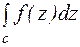. Пусть 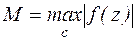, l – длина контура с. Покажем, что справедливо неравенство: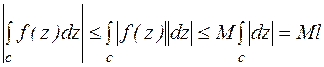

Выпишем интегральную сумму:

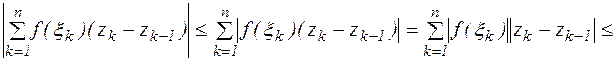
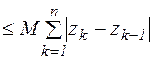(3)

Обозначим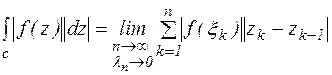

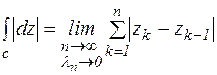
Сумма 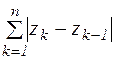задает длину ломанной линии, вписанной в контур С, тогда 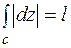. Из соотношения (3) следует неравенство:

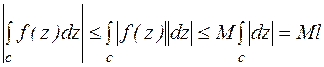
СВОЙСТВА ИНТЕГРАЛОВ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

Теорема 3. Если функция 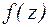аналитична в односвязной области D ,то для любых контуров С, лежащих в этой области и имеющих одни и те же концы, интеграл 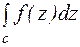имеет одно и тоже значение.

Теорема утверждает, что значение интеграла, если функция аналитична в области D, не зависит от пути интегрирования, а определяется только начальной и конечной точкой.

Доказательство: Было получено равенство

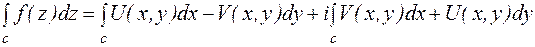
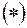
Из анализа известно, что криволинейный интеграл вида 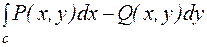не зависит от пути интегрирования, если под знаком интеграла стоит полный дифференциал. Критерием того, что под знаком интеграла стоит полный дифференциал является 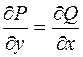. Для криволинейных интегралов из равенства 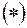это условие приводит к соотношению:

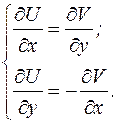
Эти условия выполняются, так как по формулировке теоремы f(z) аналитическая функция. Теорема доказана.

Так как значение интеграла не зависит от пути интегрирования, то для аналитической функции вместо записи 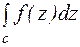можно использовать запись 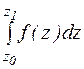, где 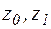- начальная и конечная точки контура.

ЛЕКЦИЯ 5

План лекции

1. Теорема об интеграле по замкнутому контуру.

2. Теорема Коши для односвязной области.

3. Теорема Коши для многосвязной области.

Теорема 4. Если функция 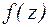аналитична в односвязной области D ,то интеграл 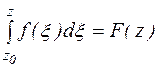, рассматриваемый как функция верхнего предела, является аналитической функцией, причем

.

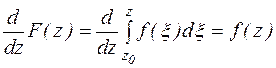Функция F(z) называется первообразной функции f(z), если .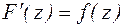

Теорема 5. Любые две первообразные одной и той же функции f(z) отличаются друг от друга на константу.

Доказательство: Пусть 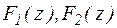- первообразные функции f(z). Составим функцию Ф(z): .

.

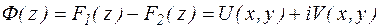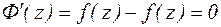С другой стороны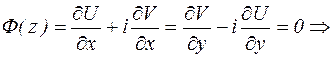

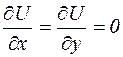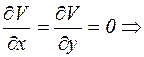
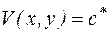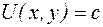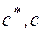, , ( -константы). 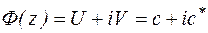- комплексная константа.

Теорема доказана.

Теорема 6.. Если функция 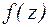аналитична в односвязной области D ,то 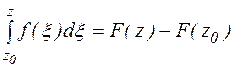(формула Ньютона - Лейбница), где F(z) – любая первообразная.

Доказательство:В соответствии с теоремой 4 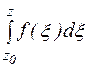является аналитической функцией и первообразной функции f(z) и поэтому отличается то функции F(z) на константу, т. е. имеет место равенство: 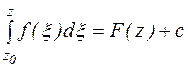(1)

Положим в равенстве (1) 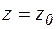, тогда получим, что 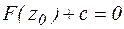, 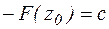. Подставляя с в равенство (1), окончательно получим:

.

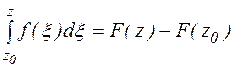Пример. Вычислить: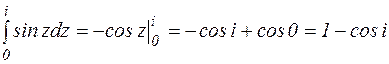

Теорема 7. Если функция 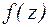аналитична в односвязной области D и с контур, целиком лежащий в области D, то .

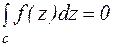Доказательство: Разобьем контур с точками a и b на два контура 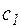и .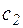

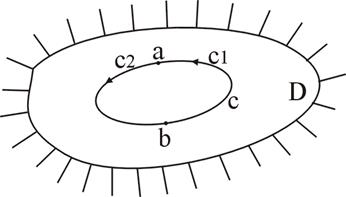Рис. 1

.

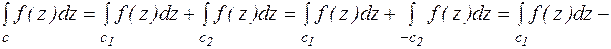
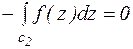Теорема 8. Если функция 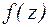аналитична в односвязной области D и непрерывна на границе с области D, то .

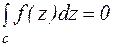Распространим теорему 8 на многосвязную область. Рассмотрим, например двухсвязную область. С помощью разреза превратим ее в односвязную область. Будем обходить границу, полученной каким образом односвязной области, в положительном направлении. За положительное направление обхода границы примем то направление, при котором область остается всегда слева. Начнем обход с точки а.

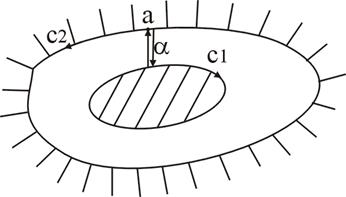Рис. 2

По теореме 8:

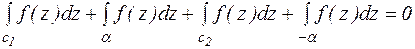
Поскольку разрез 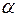проходит в двух направления, то

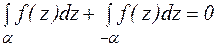
Получим равенство 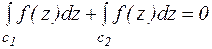. Изменим направление обхода контура 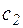на противоположное, получим 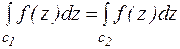. Аналогичным образом область любой связанности можно превратить в односвязную с помощью разрезов.

Теорема 9 (теорема Коши для многосвязной области) Если функция 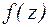аналитична в многосвязной области D и непрерывна на границе, то интеграл по внешнему контуру равен сумме интегралов внутренних контуров, при условии, что все контуры сходятся против часовой стрелки.

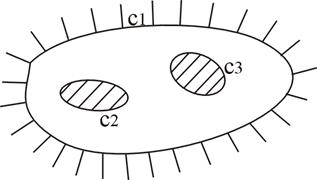Рис. 3

ЛЕКЦИЯ 6

План лекции

1. Формула Коши.

2. Формула Коши для внешних производных.

3. Применение формулы Коши для вычисления интегралов по замкнутому контуру.

4. Примеры на применение формулы Коши.

ФОРМУЛА КОШИ.

Пусть функция 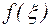аналитична в односвязной области D и непрерывна на границе с области D. Произвольно в области D выберем точку z и рассмотрим функцию 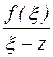. Эта функция аналитична в области D, за исключением точки 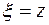, где знаменатель обращается в ноль. Выберем точку z из области D с помощью окружности .

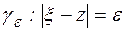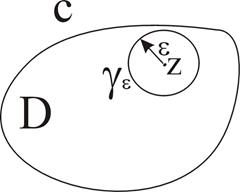Рис. 1

Функция 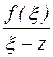является аналитичной в двухсвязной области, ограниченной контурами с и 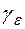. По теореме 9 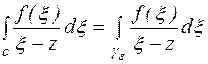(1) (обход против часовой стрелки)

Запишем тождество 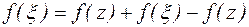и, используя его, разобьем интеграл по контуру на два интеграла.

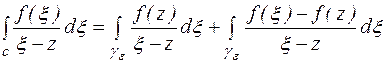(2)

Рассмотрим интеграл 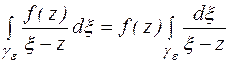. Так как контурный интеграл функции комплексного переменного сводится к двум криволинейным, то они вычисляются по тем же правилам, что и криволинейный интеграл.

На контуре 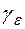: 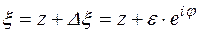, , 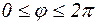тогда ,

.

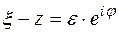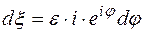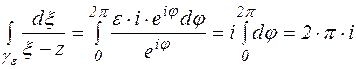
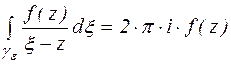
Оценим второй интеграл правой части уравнения (2).

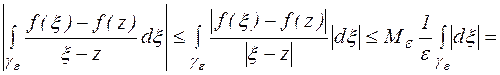
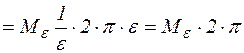
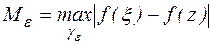
Учитывая, что функция f(z) непрерывна в области D и, следовательно, 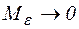при 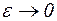, получим, что

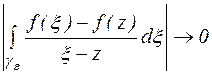при .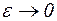

Таким образом, пренебрегаем в интеграле (2) вторым слагаемым, получаем I формулу Коши:

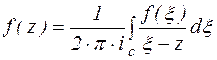(3)

Первое уравнение Коши связывает значение функции в области D со значениями на границе этой области. Для получения второго уравнения Коши, продифференцируем по z уравнение (3) n раз. Поскольку интегрирование ведется по переменной 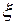, то дифференцирование интеграла сводится к дифференцированию подынтегральной функции.

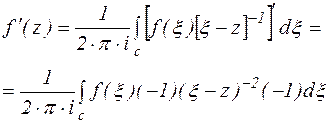
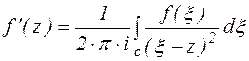
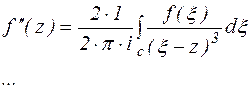
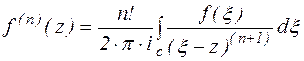(4) - II формула Коши (формула Коши для высших производных)

Формулы Коши могут быть использованы для вычисления некоторых интегралов по замкнутым контурам. В этом случае удобно заменить 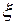на z , z на а, тогда получим:

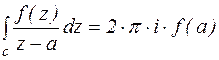(5)

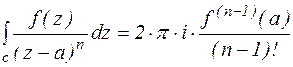(6)

Формулы справедливы, если функция f(z) аналитична в области ограниченной контуром с, а точка а, обращающая знаменатель в ноль, лежит внутри контура с.

Пример.

Вычислить интеграл по контуру с:

1. 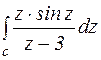, если с окружность,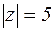

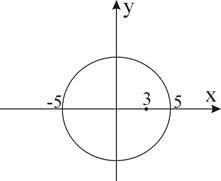рис. 2

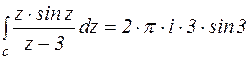
2. 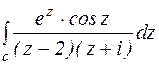, если с окружность,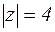

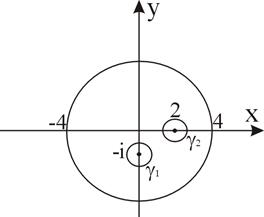рис. 3

Подынтегральная функция f(z) аналитична в области, ограниченной контурами с, 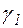, 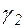. Поэтому по теореме Коши для многосвязной области получаем:

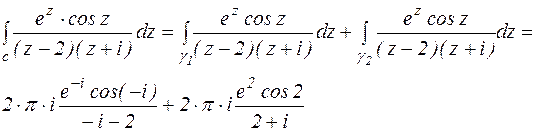
ЛЕКЦИЯ 7

План лекции

1. Ряд Тейлора.

2. Ряд Лорана.

3. Типы особых точек.

4. Особые точки и вид ряда Лорана.

5. Понятие вычета.