Етодические указания к решению задач 3 и 4. .
В результате изучения темы «Электрические цепи синусоидального тока» слушатель должен:
знать содержание терминов: резистор, сопротивление, индуктивная катушка, индуктивность, индуктивное сопротивление, конденсатор, емкость, емкостное сопротивление, фаза, начальная фаза, угол сдвига фазы, период, частота, угловая частота, мгновенное и действующее значения гармонических величин, полная, активная и реактивная мощности, коэффициент мощности;
понимать особенности энергетических процессов в электрических цепях синусоидального тока;
знать сущность резонансных явлений в цепях переменного тока и условия резонансов;
представлять гармонически изменяющиеся величины комплексными числами; уметь составлять комплексные уравнения состояния линейных цепей; строить векторные диаграммы неразветвленных цепей и цепей с параллельным соединением электроприемников.
В электротехнике простейшим переменным сигналом является гармонический (ЭДС - е(t), напряжение - (u(t), ток - i(t)).
Применяют несколько способов представления гармонических (синусоидальных – sin или косинусоидальных –cos) электрических величин.
1. Временной (аналитический) способ - ток задается аналитически в виде функции времени (1.1). Аналитически гармонический сигнал (например, напряжение) записывается выражением:
u(t) = Umsin(ω0t+φ0) , (1.1)
где u(t) – мгновенное значение напряжения – напряжение в момент времени t.
Временная диаграмма гармонического сигнала приведена на рис.1.1. Он характеризуется следующими тремя основными параметрами:
1. um – амплитуда, величина наибольшего отклонения от нуля, (В- вольт);
2. Т – период, наименьший интервал времени, по истечении которого мгновенные величины повторяются, измеряется в (сек), с ним связаны f=1/Т – циклическая частота, измеряется в (Гц) и ω0 =2πf – угловая частота - (рад/с);
3. φ0 – начальная фаза, (рад). Выражение в скобках - (ω0t+φ0)=ψ(t) называют полная фаза. Отсюда φ0 = ψ(t=0).
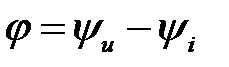
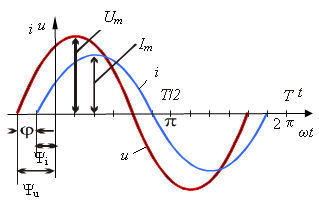
Рис. 1.2. Временные диаграммы двух гармонических сигналов
Кроме амплитуд о величине периодических сигналов судят по их среднеквадратичным (действующим) значениям за период, I, U, E –
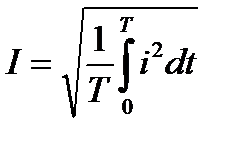 ,
, 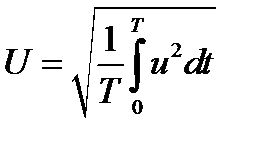 ,
, 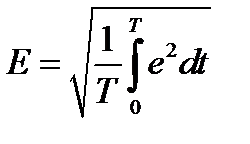 .
.
Для синусоидальных сигналов законы Кирхгофа и Ома и анализ цепей удобно проводить используя комплексную форму записи.
При комплексном представлении гармоническое колебание как функция времени заменяется комплексной амплитудой, т.е. комплексным числом, не зависящим от времени. Это делается для упрощения записи и выполнения операций над гармоническими функциями.
Комплексная амплитуда содержит информацию о двух важнейших параметрах гармонического сигнала – об амплитуде и начальной фазе. Комплексная амплитуда и гармоническая функция времени при известной частоте ω связаны взаимнооднозначно, т.е.
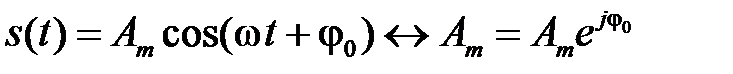 .
.
Пример 1. Например, гармоническому колебанию u(t) = 256 cos(2π100t – 45°) соответствует комплексная амплитуда 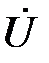 m = 256 e–j45.
m = 256 e–j45.
Справедливо и обратное. Если известна комплексная амплитуда гармонического сигнала  m = 256 e–j45 и частота ω=2π100, то этому соответствует гармоническое колебание u(t) = 256 cos(2π100t – 45°).
m = 256 e–j45 и частота ω=2π100, то этому соответствует гармоническое колебание u(t) = 256 cos(2π100t – 45°).
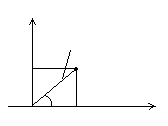 Рис. 2.9 Рис. 2.9 |
| Im |
| j0 |
| a |
| A = Öa2+b2 |
| Re |
| b |
Законы Ома и Кирхгофа в комплексной форме
Они имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин: комплексных амплитуд и комплексных сопротивлений.
1. Закон Ома.Он устанавливает связь между комплексными амплитудами тока и напряжения на участке цепи. 1.8. Закон Ома для участка цепи, не содержащего источника ЭДС (рис. 1.8):
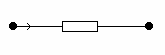 Рис. 1.8 Рис. 1.8 |
| Im |
| Z |
| j1 |
| j2 |
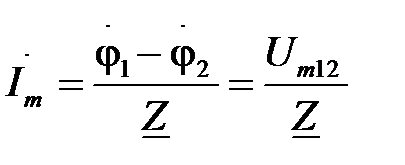 ,
, где 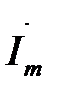 и
и 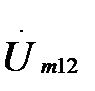 - комплексные амплитуды тока и напряжения на участке цепи; Z – комплексное сопротивление участка цепи,
- комплексные амплитуды тока и напряжения на участке цепи; Z – комплексное сопротивление участка цепи, 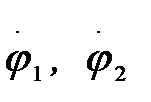 –комплексные амплитуды потенциалов на данном участке цепи.
–комплексные амплитуды потенциалов на данном участке цепи.
2. Первый закон Кирхгофа: Алгебраическая сумма комплексных амплитуд (действующих значений) токов в узле равна нулю
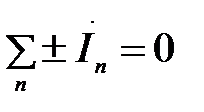 . (1.5 а)
. (1.5 а)
3. Второй закон Кирхгофа: В замкнутом контуре электрической цепи алгебраическая сумма комплексных амплитуд (действующих значений, ЭДС) равна алгебраической сумме комплексных падений напряжений в нём.
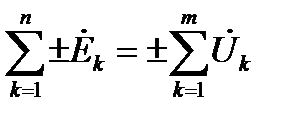 . (1.5 б)
. (1.5 б)
Комплексное сопротивление элемента (участка цепи)
Под комплексным сопротивлением понимают отношения комплексной амплитуды входного напряжения к комплексной амплитуде входного тока:
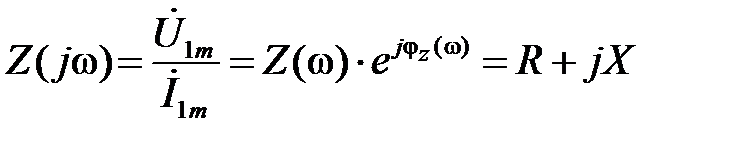 . (1.6)
. (1.6)
где Z –модуль комплексного сопротивления, φ=ψu - ψi – начальная фаза или аргумент комплексного сопротивления; R - активного сопротивления, X– реактивному сопротивлению, причем Z=(R2+X2)1/2, а φz(ω)=ψu-ψi =arctg(X/R).
По виду записи комплексного сопротивления можно судить о характере участка цепи: Z=R – активное (резистивное) сопротивление; Z=R+jX — активно-индуктивное сопротивление; Z=R – j X — активно-емкостное
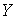 - комплексная проводимость, величина, обратная комплексному сопротивлению:
- комплексная проводимость, величина, обратная комплексному сопротивлению:
Метод комплексных амплитуд состоит в следующем:
1) исходная схема электрической цепи заменяется комплексной схемой замещения, в которой:
а) все пассивные элементы заменяются их комплексными сопротивлениями, как показано на рис. 4.27.
б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е. х(t) = Xm cos(w0t – jx) ® Xm = Xm e–jjx.
| ZL=jwL |
| L |
| ZC=1/(jwC) |
| C |
| ZR=R |
| R |

Рис. 4.27
2) Расчет электрической цепи сводится к составлению уравнений состояния цепи на основе законов Ома и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или напряжений на интересующих нас участках цепи, т.е. Ym = Ym e–jjy.
3) Запись окончательного решения состоит в замене рассчитанных комплексных амплитуд на гармонические функции времени, т.е.
Ym =Ym e –jjy ® y(t) = Ym cos(w0t – jy).
Пример 5. Алгоритм метода рассмотрим на примере анализа цепи, структура которой приведена на рис. 4.29.
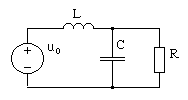
Рис. 4.29. RLC-цепь второго порядка
На вход цепи подается синусоидальное воздействие 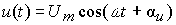 . Параметры воздействия и элементов цепи известны: Um=1 В, ω =1 с-1 , φ u=900 , R=1 Ом, L=1 Гн, C=1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.
. Параметры воздействия и элементов цепи известны: Um=1 В, ω =1 с-1 , φ u=900 , R=1 Ом, L=1 Гн, C=1 Ф. Требуется определить токи и напряжения ветвей, построить векторную диаграмму.
Решение.
1. Представим воздействие в комплексной форме:
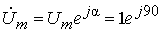 .
.
2. Построим схему замещения цепи в частотной области, заменив элементы цепи комплексными двухполюсниками, как это показано на рис. 4.30.
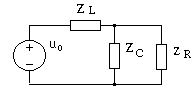
Рис. 4.30. Схема замещения цепи в частотной области
3. Произведем расчет реакций (токов и напряжений) в комплексной области. При этом можно воспользоваться законами Кирхгофа и Ома в комплексной форме, а также известными методами расчета резистивных цепей:
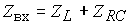 ,
, 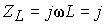 ,
, 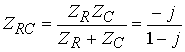 ,
,
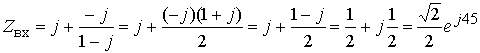 ,
,
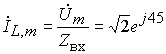 ,
, 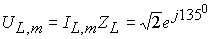 ,
,
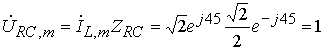 ,
,
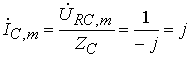 ,
, 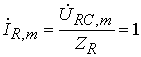 .
.
3. Построим векторную диаграмму для токов и напряжений в цепи. Для этого на комплексной плоскости откладываются в соответствующем масштабе найденные токи и напряжения, как показано на рис. 4.31.
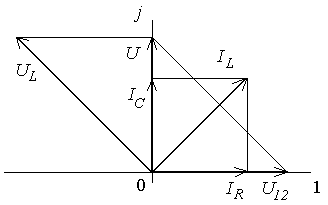
Рис. 4.31. Векторная диаграмма
Построение векторной диаграммы, как правило, является конечным результатом решения подобных задач. Векторная диаграмма показывает амплитуду и начальную фазу любого тока или напряжения. При необходимости записать временную функцию тока или напряжения, это всегда можно сделать, имея векторную диаграмму. Например, напряжение на L-элементе имеет амплитуду 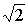 , а начальную фазу 1350, значит, во временной области это напряжение можно записать так:
, а начальную фазу 1350, значит, во временной области это напряжение можно записать так:
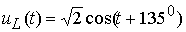 .
.
ример 2.
Активное сопротивление катушки Rк=6 Ом, индуктивное Xl=10 Ом. Последовательно с катушкой включено ативное сопротивление R=2Ом и конденсатор сопротивлением хс=4 Ом (рис.2,а). К цепи приложено напряжение U=50В ( действующее значение). Определить :1) полное сопротивление цепи;2)ток;3)коэффициент мощности;4)активную, реактивную и полную мощности;5) напряжения на каждом сопротивлении. Начертите в масштабе векторную диаграмму цепи.
Решение: 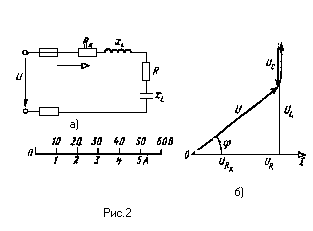
1.Определяем полное сопротивление цепи
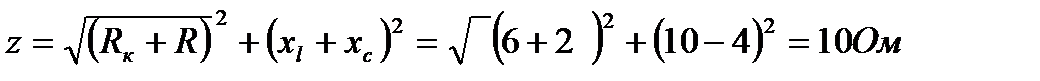
2.Определяем ток
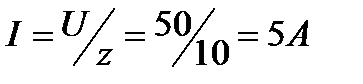
3.Определяем коэффициент мощности цепи
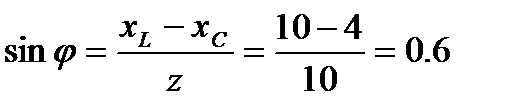
по таблицам Брадиса находим j=36050’ . Угол сдвига фаз j находим по синусу во избежание потери знака угла ( косинус является четной функцией)
4.Определяем активную мощность цепи
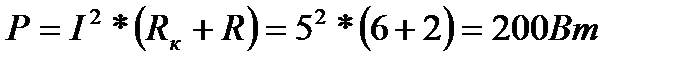
или
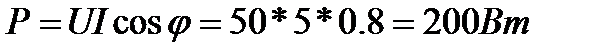
Здесь
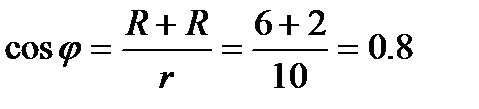
5.Определяем реактивную мощность цепи
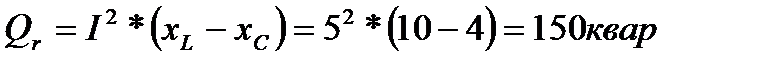
6.Определяем активную мощность цепи
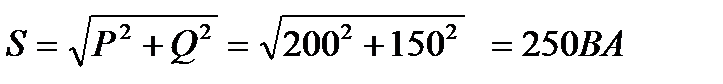
или
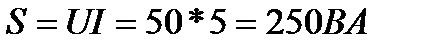
7.Определяем падение напряжения на сопротивлениях цепи
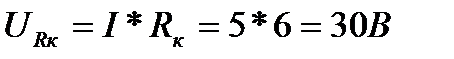 ;
; 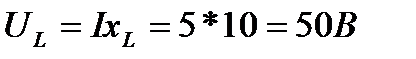 ;
; 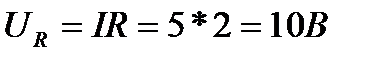 ;
;
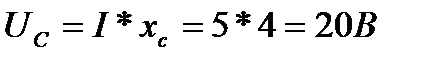
Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току : в 1см – 1,0А и масштабом по напряжению : 1см- 10В. Построение векторной диаграмм ( рис.2,.б) начинаем с вектора тока, который откладываем по горизонтали в масштабе
Вдоль вектора тока откладываем векторы падения напряжения на активных сопротивления URк и UR:
Из конца вектора UR откладываем в сторону опережения вектора тока на 900 вектор падения напряжения UL на индуктивном сопротивлении длиной 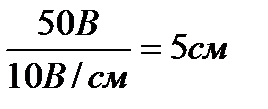 .Из конца вектора UI откладываем в сторону отставания от вектора тока на 900 вектор падения напряжения на конденсаторе UC длиной
.Из конца вектора UI откладываем в сторону отставания от вектора тока на 900 вектор падения напряжения на конденсаторе UC длиной 
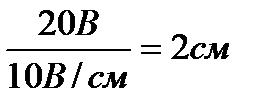 . Геометрическая сумма векторов URк, UR, UL и UC равна полному напряжению U, приложенному к цепи .
. Геометрическая сумма векторов URк, UR, UL и UC равна полному напряжению U, приложенному к цепи .
ример 3.
На рис. 3,а задана векторная диаграмма для неразветвленной цепи, ток I и падения напряжений на каждом сопротивлении ( U1, U2 и т.д.) Определить характер и величину каждого сопротивления, начертить эквивалентную схему цепи, вычислить приложенное напряжение и угол сдвига фаз j.
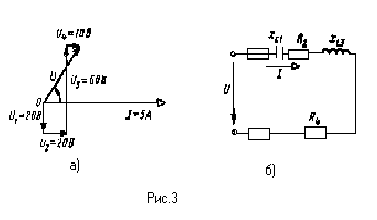
Решение:
1.Из векторной диаграммы следует, что напряжение U1 отстает от тока на угол 900. Следовательно, на первом участке включен конденсатор, сопротивление которого
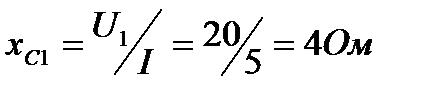
Вектор напряжение на втором участке U2 направлен параллельно вектору тока, т.е. совпадает с ним по фазе. Значит, на втором участке включено активное сопротивление
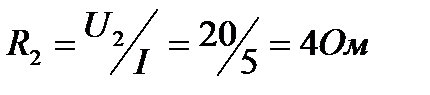
Вектор напряжения на третьем участке U3 опережает вектор тока на угол 900, что характерно для индуктивности, сопротивление которой
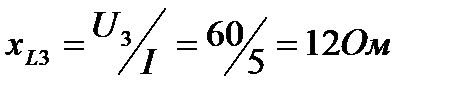
На четвертом участке включено активное сопротивление
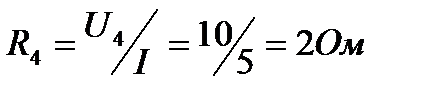
Эквивалентная схема цепи приведена на рис. 3, б.
2.Из векторной диаграммы определяем значение приложенного напряжения и угол сдвига фаз:
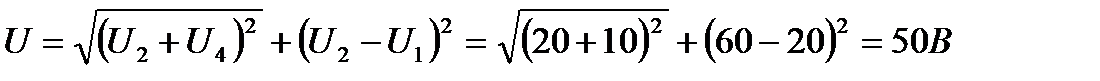 .
.
Пример:
К электрической цепи, рис. 3.12, а, подведено синусоидальное напряжение частотой f = 50 Гц с действующим значением U = 100 В. Параметры элементов схемы: R1 = 30 Ом, L = 0,1 Гн, C = 50 мкФ, R2 = 20 Ом. Определить токи в ветвях схемы и показания приборов. Составить баланс мощности. Построить в масштабе векторную диаграмму токов и напряжения.
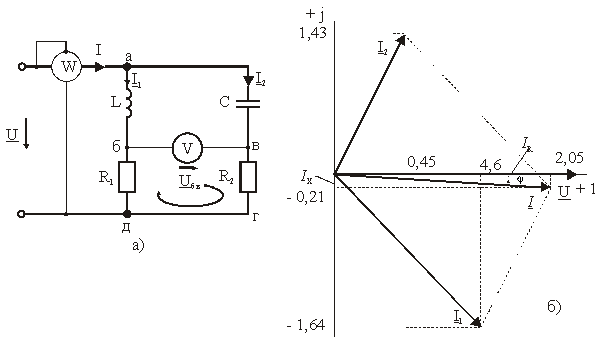
Рис. 3.12 – Параллельная цепь:
а) схема замещения; б) векторная диаграмма
Решение
Определяем комплексные сопротивления параллельных ветвей. Сопротивление первой ветви
Z1 = R1 + jXL,
где
XL = jωL = 2πfL = 6,28∙50∙0,1 = 31,4 Ом;
Z1 = 30 + j31,4 Ом.
Комплексное сопротивление второй ветви
Z2 = R2 – jXС;
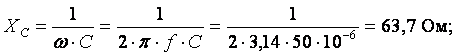
Z2 = 20 – j63,7 Ом.
Находим комплексные значения токов в ветвях
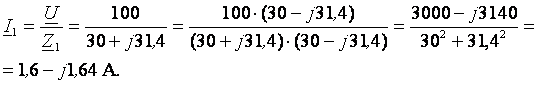
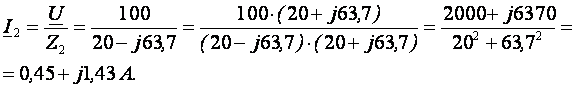
I = I1 + I2 = 1,6 – j1,64 + 0,45 + j1,43 = 2,05 – j0,21 A.
Действующие значения
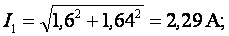
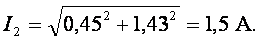
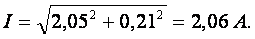
Для определения показания вольтметра составляем уравнение согласно второго закона Кирхгофа для контура б, в, г, д, б. Произвольно выбираем направление обходе контура, показанное на рис. 3.12, а стрелкой
0 = Uбв + R2I2 – R1I1;
1.. Uбв = R2I2 – R1I1 = 20·(0,45 + j1,43) – 30(1,6 – j1,64) =
= 9 + j28,6 – 48 + j49,2 = - 39 + j77,8;
Uбв = 39 – j77,8 В.
Вольтметр покажет действующее значение напряжения Uбв
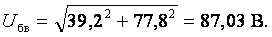
Ваттметр измеряет мощность, потребляемую активной нагрузкой (R1 и R2).
Известно, что
Р = U·I·cosφ.
В этом выражении неизвестным является cosφ, где φ угол сдвига между напряжением U и током I. Определить угол φ (или cosφ) можно разными путями. Например, cosφ можно найти из выражения для общего тока, учитывая, что начальная фаза напряжения равна нулю. Для этого обратимся к комплексному значению общего тока
I = 2,05 – j0,21 A,
где IR = 2,05 – активная составляющая тока (проекция комплексного вектора полного тока на ось действительных чисел);
IX = - j0,21 – реактивная составляющая тока (проекция комплексного вектора полного тока на ось мнимых чисел).
Тогда
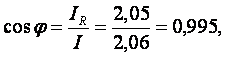
где I = 2,06 А – действующее значение общего тока.
Показание ваттметра
Р = 100∙2,06∙0,995 = 205 Вт.
Составим баланс мощностей.
Полная мощность, поступающая от источника
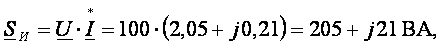
где PИ = 205 Вт; QИ = 21 Вар.
Мощности приёмников
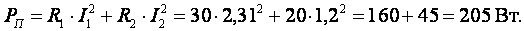
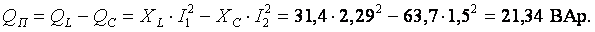
SП = РП + jQП = 205 + j21,34 ВА.
Результаты расчётов показывают, что баланс мощности сходится, т. е. токи найдены правильно.
Векторную диаграмму строим на комплексной плоскости, рис. 3.12, б. Выбираем масштабы тока и напряжения: 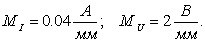 (Масштаб выбирается с таким расчётом, чтобы векторная диаграмма занимала примерно половину страницы). Откладываем вектор напряжения совпадающий с осью +1. Затем откладываем вычисленные значения токов I1, I2, I. Действительные значения – на оси +1, мнимые значения – на оси +j.
(Масштаб выбирается с таким расчётом, чтобы векторная диаграмма занимала примерно половину страницы). Откладываем вектор напряжения совпадающий с осью +1. Затем откладываем вычисленные значения токов I1, I2, I. Действительные значения – на оси +1, мнимые значения – на оси +j.
Контрольные вопросы к экзамену (зачету)
Контрольные вопросы к зачету (экзамену ) по разделу "Основы электротехники".
1. Электробезопасность. Характеристики поражения человека электрическим током.
2. Основные определения: электротехника, электричество, электрическое поле, потенциал, напряжение, электрический ток, источники тока , электродвижущая сила (ЭДС), закон Ома , законы Кирхгофа.
3. Электрическая цепь. Пассивные и активные элементы цепи. Параметры электрической цепи.
4. Расчет электрических цепей постоянного тока методом законов Кирхгофа, методом контурных токов.
5. Энергия и мощность постоянного тока. Баланс мощностей.
6. Переменный ток. Однофазный синусоидальный ток. Основные параметры: мгновенные, действующие и средние значения тока, напряжения и ЭДС. Генерирование переменного тока.
7. Представление переменного тока комплексными величинами. Метод комплексных диаграмм.
8. Метод комплексных амплитуд. Закон Ома и законы Кирхгофа в комплексной форме.
9. Активное сопротивление, индуктивность и емкость в цепи переменного тока.
10. Последовательная и разветвленные цепи переменного тока с активным сопротивлением, емкостью и индуктивностью. Резонанс тока. Резонанс напряжения.
11.Мощность и энергия в цепи переменного тока. Активная, реактивная и полная мощность. Единицы измерения. Баланс мощностей.
12.Трехфазные электрические цепи. Основные определения. Линейные и фазные токи и напряжения. Маркировка фазы. Способы соединения генераторов и приемников типа звезда и треугольник. Трехпроводные и четырехпроводные цепи. Нейтральный провод.
13. Короткое замыкание фазы. Разрыв линейного провода. Мощность в цепи трехфазного тока.
14. Нелинейные электрические цепи. Аппроксимация нелинейных характеристик.
15. Расчет цепей постоянного тока с одним или несколькими нелинейными элементами.
16. Основные магнитные величины. Магнитные цепи постоянного тока.
17. Магнитные цепи переменного тока. Ферромагнитные материалы.
18. Расчет катушки с магнитопроводом и воздушным зазором.
19. Энергия и основные потери в магнитопроводе.
20 Трансформатор. Основные режимы работы.
21. Устройство и принцип действия машин постоянного тока.
22. Генератор постоянного тока. Основные характеристики.
23.Двигатель постоянного тока. Основные характеристики.
24.Устройство и принцип действия машины переменного тока.
25. Асинхронный двигатель. Основные характеристики.
26. Синхронный генератор. Основные характеристики.
емы рефератов.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Самостоятельная работа студентов состоит в изучении ряда теоретических вопросов по темам дисциплины, перечень которых приведен в таблице 5 и составления рефератов..
Таблица 5
| № п/п | Тема дисциплины |
| Тема 1. Электрические цепи. Основные определения, топологические параметры | |
| Тема 2. Методы расчета линейных электрических цепей | |
| Тема З. Однофазный переменный ток | |
| Тема 4. Электрические цепи трехфазного тока. | |
| Тема 5. Магнитные цепи и электромагнитные устройства. | |
| Тема 6. Трансформаторы | |
| Тема 7. Асинхронные машины | |
| Тема 8. Машины постоянного тока (МПТ) | |
| Тема 9. Синхронные машины | |
| Тема 10. Электрические измерения и приборы | |
| Тема 11. Основы электроники и элементной базы современных электронных устройств | |
| Тема 12. Источники вторичного электропитания | |
| Тема 13. Усилители электрических сигналов | |
| Тема 14. Импульсные и автогенераторные устройства | |
| Тема 15. Основы цифровой электроники | |
| Тема 16. Микропроцессорные средства |
