Задания для самостоятельной работы.

Теория.

Приращение 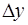функции 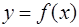представимо в виде:

,

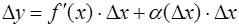где функция 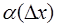является бесконечно маленькой функцией при стремлении аргумента 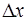к нулю.

Так как 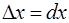, то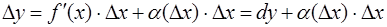

В силу того, что второе слагаемое 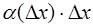является бесконечно малым, то им можно пренебречь, а поэтому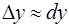

А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.

Для приближенного вычисления значения функции применяется следующая формула: .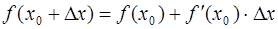

Пример 1. Вычислить приближенно 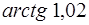, заменяя приращение функции ее дифференциалом.

Решение:

· Рассмотрим функцию 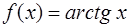. Необходимо вычислить ее значение в точке .

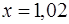· Для приближенного вычисления значения функции применяется следующая формула: .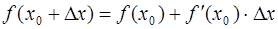

· Величину х представим в виде 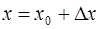, т. е. 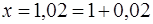, тогда , .

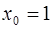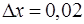· Вычислим значение функции 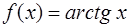в точке : .

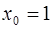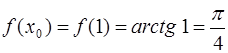· Продифференцируем рассматриваемую функцию: .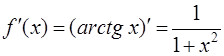

· Найдем значение : .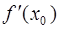

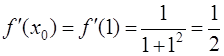· Итак,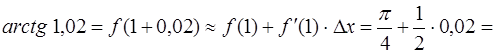

.

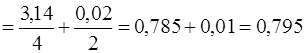Ответ. .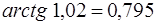

Пример 2.С помощью дифференциала вычислить приближенно .

Решение:

· Рассмотрим функцию 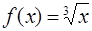. Необходимо вычислить ее значение в точке .

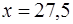· Для приближенного вычисления значения функции применяется следующая формула: .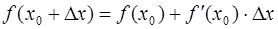

· Величину х представим в виде 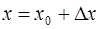, т. е. 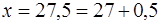, тогда , .

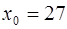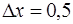· Вычислим значение функции 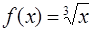в точке :

.

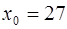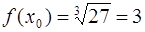· Продифференцируем рассматриваемую функцию: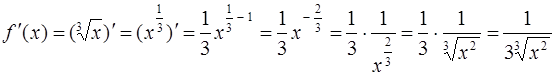

· Найдем значение : .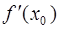

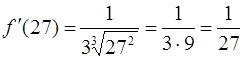· Подставляя все в формулу, окончательно получим: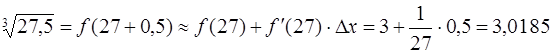

Ответ.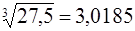

Пример 3. С помощью дифференциала вычислить приближенно .

Решение:

· Рассмотрим функцию 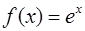. Необходимо вычислить ее значение в точке .

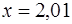· Для приближенного вычисления значения функции применяется следующая формула: .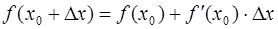

· Величину х представим в виде 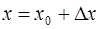, т. е. 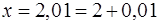, тогда , .

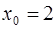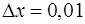· Вычислим значение функции 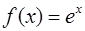в точке :

.

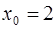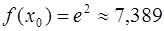· Продифференцируем рассматриваемую функцию: .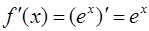

· Найдем значение : .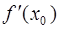

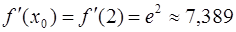· Подставляя все в формулу, окончательно получим: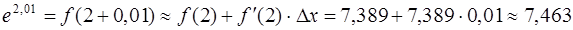

Ответ.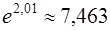

Пример 4. С помощью дифференциала вычислить приближенно .

Решение:

· Рассмотрим функцию 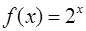. Необходимо вычислить ее значение в точке .

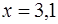· Для приближенного вычисления значения функции применяется следующая формула: .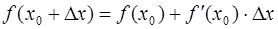

· Величину х представим в виде 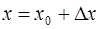, т. е. 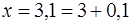, тогда , .

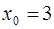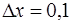· Вычислим значение функции 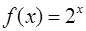в точке :

.

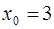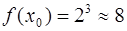· Продифференцируем рассматриваемую функцию: .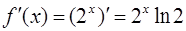

· Найдем значение : .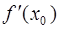

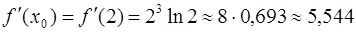· Подставляя все в формулу, окончательно получим: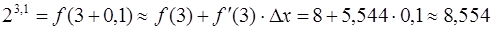

Ответ.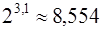

Пример 5.С помощью дифференциала вычислить приближенно .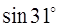

Решение:

· Рассмотрим функцию 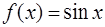. Необходимо вычислить ее значение в точке .

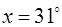· Для приближенного вычисления значения функции применяется следующая формула: .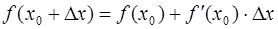

· Величину х представим в виде 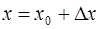, т. е. 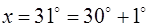, тогда , .

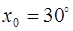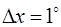· Переведём градусы в радианы: ,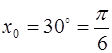

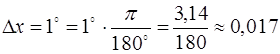
· Вычислим значение функции 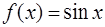в точке :

.

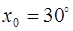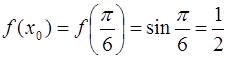· Продифференцируем рассматриваемую функцию: .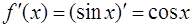

· Найдем значение :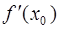

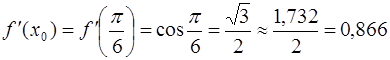
· Подставляя все в формулу, окончательно получим: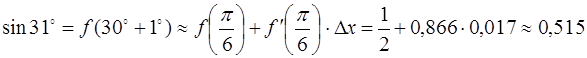

Ответ.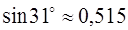

Задания для самостоятельной работы.