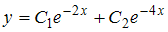Дифференциальные уравнения первого порядка с разделяющимися переменными
Дифференциальные уравнения первого порядка с разделяющимися переменными.
3. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
4. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
5. Линейные дифференциальные уравнения первого порядка.
6. Однородные дифференциальные уравнения.
Основные понятия теории дифференциальных уравнений.
ПРИМЕР Частными решениями дифференциального уравнения 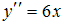 являются …
являются …
 | 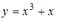 | ||
 | 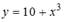 | ||
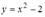 | |||
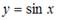 |
Решение:
Можно проверить каждую из данных функций.
1) 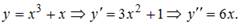 Подставим
Подставим 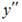 в данное уравнение.
в данное уравнение. 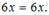 Получили тождество, и, значит,
Получили тождество, и, значит, 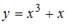 является решением данного уравнения.
является решением данного уравнения.
2) 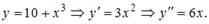 Подставим
Подставим 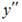 в данное уравнение.
в данное уравнение. 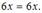 Получили тождество, и, значит,
Получили тождество, и, значит, 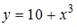 является решением данного уравнения.
является решением данного уравнения.
3) 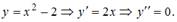 Подставим
Подставим 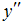 в данное уравнение.
в данное уравнение.
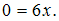 Тождество не получилось. Значит,
Тождество не получилось. Значит, 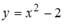 не является решением уравнения.
не является решением уравнения.
4) 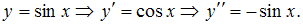 Подставим
Подставим 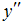 в данное уравнение.
в данное уравнение. 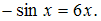 Тождество не получилось. Значит,
Тождество не получилось. Значит, 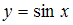 не является решением уравнения.
не является решением уравнения.
1.Общим решением дифференциального уравнения 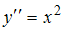 является …
является … 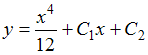
2.Частными решениями дифференциального уравнения
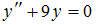 являются …
являются … 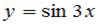 ,
, 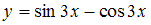
2.Общим решением уравнения 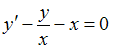 является …
является … 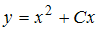
3.Частными решениями дифференциального уравнения 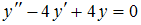 являются …
являются …
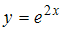 | 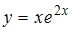 | ||
| Не являются | 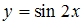 | ||
| , | 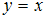 |
4.Частными решениями дифференциального уравнения 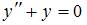 являются …
являются …
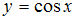 | , | 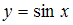 |
Дифференциальные уравнения первого порядка с разделяющимися переменными
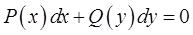 Решение:
Решение: 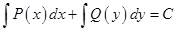
Пример1: Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 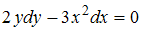 является …
является …
Решение:
Проинтегрируем обе части уравнения: 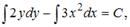 получим:
получим: 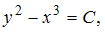 где
где 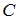 − любое число.
− любое число.
Пример 2: Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 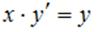 является …
является …
Решение:
Так как 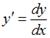 , то получаем уравнение
, то получаем уравнение 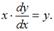
Данное уравнение равносильно уравнению 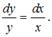
Тогда 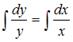 . Получаем
. Получаем 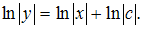
Ответ можно записать так: 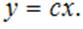
1.Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 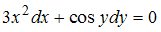 является …
является … 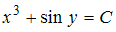
2.Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 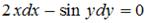 является …
является … 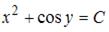
3.Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 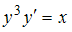 является …
является … 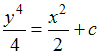
4.Решением (общим интегралом) дифференциального уравнения с разделяющимися переменными 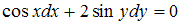 является …
является …
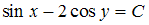 |
| 3.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами | ||||||
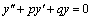 Квадратное уравнение Квадратное уравнение 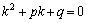 , из которого определяется число k, называется характеристическим уравнением , для составления характеристического уравнения достаточно в дифференциальном уравнении производные , из которого определяется число k, называется характеристическим уравнением , для составления характеристического уравнения достаточно в дифференциальном уравнении производные 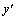 и и 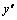 заменить на k и заменить на k и 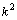 , а функцию y на единицу. Решим характеристическое уравнение. , а функцию y на единицу. Решим характеристическое уравнение. 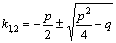 составим таблицу, использование которой облегчает отыскание общего решения уравнения составим таблицу, использование которой облегчает отыскание общего решения уравнения 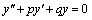 . .
Пример1: Общим решением дифференциального уравнения Составим характеристическое уравнение: Пример2: Решить дифференциальное уравнение
Решение. Составим характеристическое уравнение этого дифференциального уравнения: Приме3:Составить общее решение дифференциального уравнения Решение. Составим характеристическое уравнение и найдем его корни | ||||||
1.Общим решением дифференциального уравнения 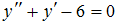 является … является … 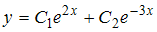
|
| 4.Дифференциальные уравнения высших порядков, допускающие понижение порядка |
Пример1: Общим решением дифференциального уравнения 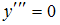 является …
является …
Решение:
Можно три раза проинтегрировать данное уравнение, тогда 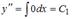 .
. 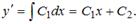
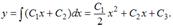 Учитывая произвольность
Учитывая произвольность 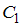 , ответ можно записать в виде
, ответ можно записать в виде 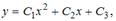 где
где 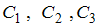 – любые числа.
– любые числа.
Пример 2: Общим решением дифференциального уравнения 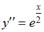 является …
является …
Решение:
Можно два раза проинтегрировать данное уравнение, тогда получим: 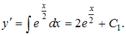
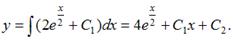
1.Общим решением дифференциального уравнения 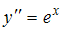 является …
является …

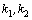
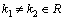
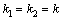
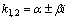
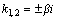
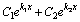
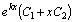
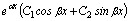

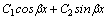
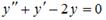 является …
является …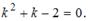

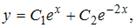 где
где 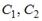 – любые числа.
– любые числа.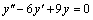 .
.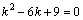 . Тогда
. Тогда 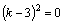 и
и 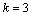 . Общее решение данного дифференциального уравнения составляем по формуле (2):
. Общее решение данного дифференциального уравнения составляем по формуле (2): 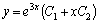 .
.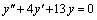
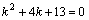 ,
, 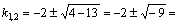
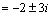 . Тогда согласно формуле (3) получаем общее решение данного дифференциального уравнения
. Тогда согласно формуле (3) получаем общее решение данного дифференциального уравнения 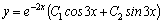 .
.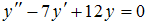 является …
является … 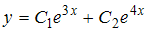 3.Общим решением дифференциального уравнения
3.Общим решением дифференциального уравнения 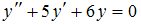 является …
является … 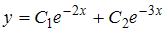 4.Общим решением дифференциального уравнения
4.Общим решением дифференциального уравнения 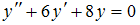 является …
является …