Управление в условиях неопределенности

Альтернативы – то, что мы выбираем (пути или варианты решения проблемы). А то, к чему мы приходим в результате реализации альтернатив, называют исходами.

Различают 3 основных типа зависимости исходов от альтернатив (3 типа связей между ними):

1. Простейший тип связи, когда каждая альтернатива приводит к единственному исходу. В этом случае имеет место функциональная зависимость исходов от альтернатив, и решение принимается в условиях определенности.

2. Более сложный тип связи, когда каждая альтернатива может привести к одному из нескольких исходов, каждый из которых может произойти с определенной вероятностью. В этом случае имеет место стохастическая зависимость исходов от альтернатив, и решение принимается в условиях риска.

3. Самый сложный тип связи, когда каждая альтернатива может привести к одному из нескольких исходов, а количественная мера возможности появления последних отсутствует (нет количественной информации). В этом случае имеет место неопределенный тип связи исходов с альтернативами, и решение принимается в условиях неопределенности.

При управлении производством принимать решения очень часто приходится, не имея достаточной информации, то есть в условиях неопределенности и риска.

Методами обоснования решений в условиях неопределенности и риска занимается математическая теория игр.

В теории игр рассматриваются такие ситуации, когда имеются 2 участника выполнения операции, каждый из которых преследует противоположные цели. В качестве участников могут выступать коллективы, конкурирующие предприятия и т.д. Во всех случаях предполагается, что операция проводится против разумного противника (конкурента), преследующего свои собственные цели и сознательно противодействующего достижению цели другим участником.

Так как цели противоположны, а результат мероприятия каждой из сторон зависит от действий конкурента, то эти действия называют конфликтными ситуациями. В конфликтной ситуации сталкиваются противоположные интересы двух участников. Формализованная (схематизированная) модель конфликтной ситуации называется игрой. Результат игры – победа или поражение, которые не всегда имеют количественное выражение, можно выразить (условно) числами.

Игра называется игрой с нулевой суммой, если один из игроков выигрывает ровно столько, сколько проигрывает другой.

Развитие игры во времени представляется как ряд последовательных «ходов». Ходы могут быть сознательные и случайные. Случайный ход – результат, получаемый не решением игрока, а каким-либо механизмом случайного выбора (покупательский спрос, задержка с поставкой материала и т.п.). Сознательный ход – выбор игроком одного из возможных вариантов действия (стратегии) и принятие решения о его осуществлении.

Возможные варианты (исходы) игры сводятся в прямоугольную таблицу (см.табл.1) – платежную матрицу, в которой строки соответствуют различным стратегиям игрока А, столбцы – стратегиям игрока В, q_ij – называется ценой игры.

Таблица 1

	B1	B2	…	Bn
A1	q11	q12	…	q1n
A2	q21	q22	…	q2n
…	…	…	…	…
Am	qm1	qm2	…	qmn

Цель теории игр – выработка рекомендаций для различного поведения игроков в конфликтной ситуации, то есть выбор оптимальной стратегии поведения для каждого из них.

Для нахождения оптимальной стратегии необходимо проанализировать все возможные стратегии и рассчитывать на то, что разумный противник на каждую из них будет отвечать такой, при которой выигрыш игрока А минимален. Обычно минимальные числа в каждой строке обозначаются 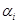и выписываются в виде добавочного столбца матрицы (см. табл.2).

Таблица 2

	B1	B2	…	Bn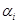
A1	q11	q12	…	q1n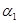
A2	q21	q22	…	q2n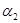
…	…	…	…	…	…
Am	qm1	qm2	…	qmn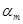
			…

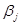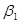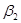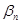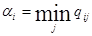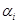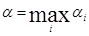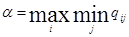В каждой строке будет свое . Предпочтительной для игрока А является стратегия, при которой обращается в максимум, то есть: или , где 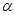- максиминный выигры (максимин), а соотвествующая ей стратегия – максиминная.

Если придерживаться максиминной стратегии, то при любом поведении стороны В (конкурента) гарантирован выигрыш, во всяком случае не меньше 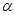. Поэтому 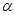называют также ценой игры – тот гарантированный минимум, который можно обеспечить при наиболее осторожной (перестраховочной) стратегии.

Очевидно, что аналогичные распределения можно провести и для конкурента В, который должен рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения выигрыша: 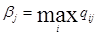(последняя строка матрицы).

Из всех значений 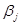находят минимальное: 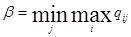, которое дает минимаксный выигрыш, или минимакс.

Такая 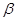-стратегия – минимаксная, придерживаясь которой сторона В гарантирована, что в любом случае проигрывает не больше 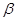. Поэтому 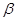называют верхней ценой игры.

Если 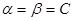, то число С называют чистой ценой игры или седловой точкой.

Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.

Пример. Конструктор получил задание разработать определенное новое изделие. В результате исследований он определил 3 возможных варианта изделия V₁, V₂, V₃, каждый из которых может быть реализован каким-либо из трех технологических процессов Т₁, Т₂, Т₃.

Если первый вариант конструкции V₁ реализуется по первой технологии Т₁, то внешний вид изделия оказывается наилучшим и оценивается экспертами в 9 баллов, а при реализации по второй технологии – в 6 баллов, по третьей – в 5 баллов и т.д. (см. табл.3).

Таблица 3

Конструкция	Технология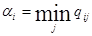
Т1	Т2	Т3
V1				5 (Т3)
V2				7 (Т2 или Т3)
V3				5 (Т2)

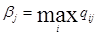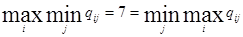Решение. Конфликтная ситуация возникает из-за того, что затраты на реализацию каждого конструкторско-технологического решения (варианта) не одинаковы. Для простоты полагаем, что затраты пропорциональны внешнему виду (чем выше балл, тем больше затраты).

Конструктор должен представить только один вариант, конечно, самый красивый. Но он понимает, что тогда найдутся сторонники самого дешевого варианта («экономисты»). Поэтому его задача – выбрать оптимальный вариант по внешнему виду и стоимости.

Если конструктор выберет V₁, то экономисты будут настаивать на технологии Т₃. На вариант V₂ будет ответ Т₂ или Т₃ и т.д.

Очевидно, что с точки зрения конструктора преимущество имеет вариант V₂, так как даже при неблагоприятных обстоятельствах получится изделие, оцениваемое в 7 баллов (выигрыш 7), а может быть, даже 8, если удается уговорить экономистов на вариант Т₁.

С точки зрения экономистов в смысле снижения затрат: при выборе технологии Т₁ в варианте V₁ затраты наибольшие – 9 баллов, при Т₂ в V₂ (7), при Т₃ в V₃ (8), то есть для экономистов оптимальным является технологический процесс Т₂, так как он требует меньших затрат при различных вариантах конструкции. Следовательно, стратегия Т₂V₂ с выигрышем 7 – наиболее выгодная сразу для обеих сторон – максимальный выигрыш V совпадает с минимальным проигрышем Т.

Однако не все матрицы имеют седловую точку. Тогда решение находят, применяя смешанные стратегии, то есть, чередуя случайным образом несколько чистых стратегий (гибкая тактика).

Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называют смешанной стратегией данного игрока.

Из этого определения следует, что сумма компонент этого вектора равна единице, а сами компоненты неотрицательны.

Обычно смешанную стратегию первого игрока обозначают как вектор U = (u₁, u₂, …, u_m), а второго игрока – как вектор Z = (z₁, z₂, …, z_m), где ,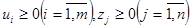

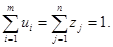
Если u⁰ – оптимальная стратегия первого игрока, z⁰ – оптимальная стратегия второго игрока, то число 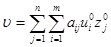называют ценой игры.

Для того, чтобы число 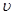- было ценой игры, а u⁰ и z⁰ – оптимальными стратегиями, необходимо и достаточно выполнение неравенств:

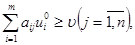
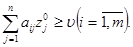
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры 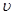вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии.