Условие линейной зависимости трех векторов
Теорема. Три вектора 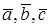 линейно зависимы тогда и только тогда, когда они компланарны.
линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство необходимости условия. Дано: 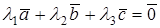 , где
, где 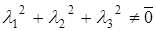 . Пусть
. Пусть 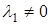 , тогда можно записать, что
, тогда можно записать, что 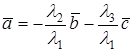 или
или 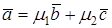 , где
, где 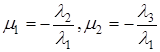 . Таким образом, вектор
. Таким образом, вектор  является диагональю параллелограмма, построенного на векторах
является диагональю параллелограмма, построенного на векторах 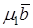 и
и 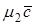 , т.е. векторы
, т.е. векторы 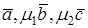 компланарны, но
компланарны, но 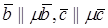 , следовательно, компланарны и векторы
, следовательно, компланарны и векторы 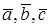 .
.
Доказательство достаточности условия. Пусть векторы 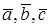 компланарны. Если среди них есть коллинеарные, то они уже линейно зависимы. Например, если
компланарны. Если среди них есть коллинеарные, то они уже линейно зависимы. Например, если 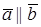 , то
, то 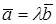 и
и 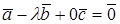 .
.
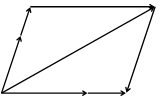 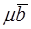 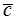 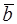 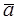 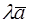 Рис. 11. Рис. 11. |
Если среди векторов 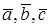 нет коллинеарных, то приводим их к общему началу и строим параллелограмм с диагональю, например, совпадающим с вектором
нет коллинеарных, то приводим их к общему началу и строим параллелограмм с диагональю, например, совпадающим с вектором 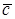 , и сторонами параллельными
, и сторонами параллельными  и
и 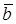 (рис. 11). Тогда
(рис. 11). Тогда 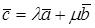 , откуда
, откуда 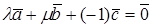 , где
, где
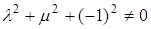 , т.е. векторы
, т.е. векторы 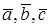 линейно зависимы.
линейно зависимы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какое выражение называется линейной комбинацией векторов?
2. Какие векторы называются линейно зависимыми и какие линейно независимыми?
3. Сформулируйте условия линейной зависимости двух векторов, трех векторов.
§3. РАЗЛОЖЕНИЕ ВЕКТОРА НА СОСТАВЛЯЮЩИЕ
Теорема 1. Если векторы  и
и 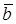 линейно независимы (неколлинеарны), то любой вектор
линейно независимы (неколлинеарны), то любой вектор 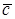 , лежащий в плоскости векторов
, лежащий в плоскости векторов  и
и 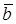 , единственным образом представляется в виде
, единственным образом представляется в виде 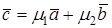 .
.
Выражение 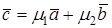 называется разложением вектора
называется разложением вектора 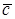 на составляющие по направлениям векторов
на составляющие по направлениям векторов  и
и 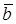 .
.
Доказательство. Дано: векторы  и
и 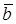 независимы, векторы
независимы, векторы 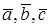 компланарны. Так как векторы
компланарны. Так как векторы 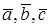 компланарны, то существуют числа
компланарны, то существуют числа 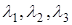 такие, что
такие, что 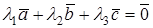 и
и 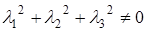 . Коэффициент
. Коэффициент 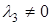 , так как в противном случае получим, что векторы
, так как в противном случае получим, что векторы 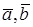 линейно зависимы, поэтому из последнего равенства имеем:
линейно зависимы, поэтому из последнего равенства имеем: 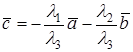 или
или 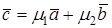 , где
, где 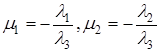 .
.
Докажем единственность такого разложения. Предположим, что существует два разных разложения вектора 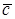 по направлениям векторов
по направлениям векторов  и
и 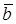 :
: 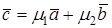 и
и 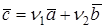 . Вычитая из одного равенства другое, получим
. Вычитая из одного равенства другое, получим 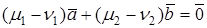 . Так как векторы
. Так как векторы  и
и 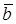 линейно независимы, то последнее равенство возможно только при
линейно независимы, то последнее равенство возможно только при 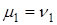 и
и 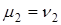 , т.е. разложение вектора
, т.е. разложение вектора 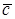 по направлениям векторов
по направлениям векторов  и
и 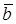 единственно.
единственно.
Теорема 2. Если три вектора 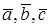 линейно независимы (некомпланарны), то любой четвертый вектор
линейно независимы (некомпланарны), то любой четвертый вектор 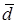 единственным образом представляется в виде
единственным образом представляется в виде 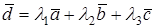 (разложение вектора
(разложение вектора 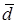 на составляющие по направлениям векторов
на составляющие по направлениям векторов 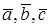 ).
).
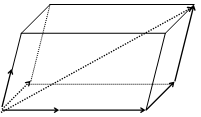 D D 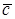 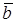 C A C A  B Рис. 12. B Рис. 12. |
Доказательство. Дано: Некомпланарные векторы 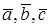 и вектор
и вектор 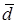 . Все векторы приводим к общему началу и строим параллелепипед со сторонами, параллельными векторам
. Все векторы приводим к общему началу и строим параллелепипед со сторонами, параллельными векторам 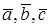 , и с диагональю, совпадающей с вектором
, и с диагональю, совпадающей с вектором 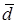 (рис.12). Имеем
(рис.12). Имеем 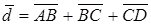 .
.
Так как 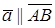 , то существует число
, то существует число
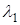 , такое, что
, такое, что 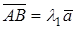 , аналогично,
, аналогично, 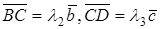 , откуда
, откуда 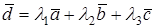 .
.
Единственность разложения доказывается аналогично плоскому случаю.
Следствие. В пространстве любые четыре вектора линейно зависимы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Докажите теоремы о разложении вектора на две, на три составляющие.
§4. ВЕКТОРНЫЙ БАЗИС, КООРДИНАТЫ ВЕКТОРА
Любая упорядоченная тройка некомпланарных векторов образует базис трехмерного пространства; упорядоченная пара неколлинеарных векторов образует базис на плоскости.
Пусть в пространстве выбран базис: 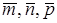 ; тогда любой вектор
; тогда любой вектор  единственным образом можно разложить на составляющие по базисным векторам:
единственным образом можно разложить на составляющие по базисным векторам: 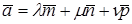 Таким образом, базис устанавливает взаимно однозначное соответствие между векторами пространства и упорядоченными тройками чисел
Таким образом, базис устанавливает взаимно однозначное соответствие между векторами пространства и упорядоченными тройками чисел 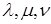 , которые называются координатами вектора в заданном базисе. Вместо записи
, которые называются координатами вектора в заданном базисе. Вместо записи 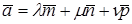 используется так же символическая запись
используется так же символическая запись 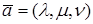 или
или 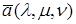 .
.
Если базисные векторы – единичные (орты) и попарно ортогональны, то базис называется ортонормированным, а базисные векторы обозначаются 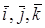 . Пусть некоторый вектор
. Пусть некоторый вектор  имеет в этом базисе координаты
имеет в этом базисе координаты 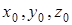 , тогда
, тогда 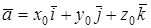 или используется символическая запись
или используется символическая запись 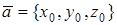 .
.
Базисные векторы в пространстве образуют правую тройку, если поворот на наименьший угол от первого вектора ко второму происходит против часовой стрелки, если смотреть с конца третьего вектора (рис. 13). В противном случае тройка векторов называется левой.
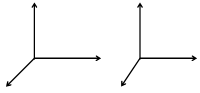 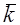 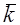 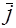 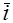 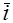 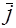 Рис. 13. Рис. 13. |
В дальнейшем используются только правые тройки.
Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными операциями над числами (координатами этих векторов).
РАВЕНСТВО ВЕКТОРОВ ПРИ ЗАДАННОМ БАЗИСЕ
Два вектора в любом базисе равны тогда и только тогда, когда равны их одноименные координаты. Это следует из взаимно однозначного соответствия между вектором и его координатами.
