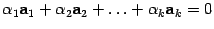Опр. линейной зависимости векторов

Векторы. Операции, свойства

Операции: 1)сложение (правило цепочки, параллелограмма, параллелепипеда)

1) вычитание –не является отдельной операцией,это всего лишь вид сложения,Герман)

3) умн. на число

Опр. линейной зависимости векторов

Система векторов 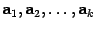называется линейно зависимой, если существует такой набор коэффициентов 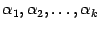, из которых хотя бы один отличен от нуля, что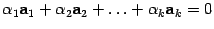

Опр. линейной независимости векторов.

Система векторов 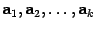называется линейно независимой, если равенство 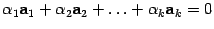возможно только при .

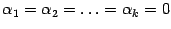Теоремы о линейной зависимости векторов.

Т1. Если в сист. х1,…хn хоть один элемент равен нулю, то система линейно-зависима.

Д-во: сост. лин. комб., которая будет нетрив. и равно нулю.

Пусть х1=0, тогда @1=12, @2=@3=@n=0

@1*x1(=0)+….=0

Т2. Если система х1..хn содержит лин-зав. подсистему х1..хm (m<n), то исходная система тоже линейно-зависима.

Базис в пространстве. Декартов базис.

Если векторы 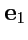, , 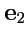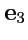взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как , , .

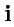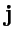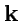Тройка векторов наз. ПРАВОЙ, если с конца в.С поворот по наим.углу от в. А к в.Б видел против час.стрелки.

Декартова система координат

-наз. совокупность фиксированной точки и ортонормированного базиса.

ОМ- радиус-вектор ДСМ

Проекция вектора на ось.

Ось-прямая линия с указ. на ней направлением и с нач.отсчета

Прокцией вект.а на ось l – длина вект.а, начало и конец которого получены с помощью проектирования на ось l начала и конца а.
Если проекция а и ось колл., то проекция «+»

Если неколлинеарны, то проекция с «-».

Углы, образ а и осями. Кос этих углов- направляющие косинусы.( являются координатами ортовектора).

Геом. смысл координат вектора.

Геометрический смысл линейной зависимости 2-х векторов

Система векторов и линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

Пусть система векторов , } линейно зависима, докажем, что || .

По свойству хотя бы один из векторов или выражается через другой, пусть = α, но это в силу определения коллинеарных векторов приводит к коллинеарности векторов || .

Скалярное произведение векторов. Определение.

а на б –это число, равное произ-ю длин перемножаемых векторов на кос. угла между ними.

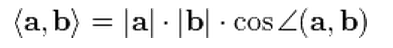
Свойства скалярного произведения

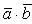
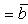
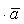
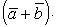
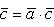
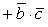
а перпенд. bóa*b=0

a*a=|a|^2
a^2=0 ó a=0

cos(a,b)= a*b/ |a|*|b|

Формула длины вектора в декартовом базисе.

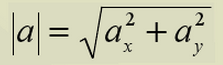на плоскости

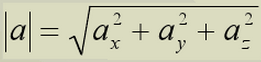в пространстве

17)Условие ортогональности 2х векторов

Скалярное произведение векторов в декартовом базисе

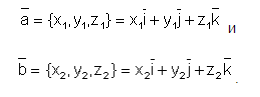
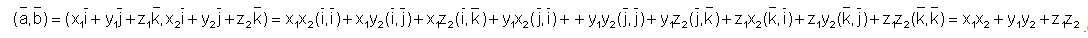
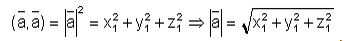
Параллельность плоскостей

Классическое определение

Две плоскости называются параллельными, если они не имеют общих точек.

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей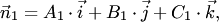

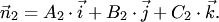
Свойства и признаки

§ Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны

§ Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

§ Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну

§ Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны

§ Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях

38)Необходимым и достаточным условием параллельности или совпадения плоскостей является условие коллинеарности их нормалей 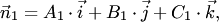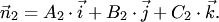Следовательно, если плоскости (4.23) параллельны или совпадают, то 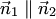т.е. существует такое число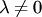

39) Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

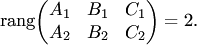
(4.25)

При этом условии система уравнений:

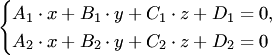
имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е.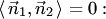

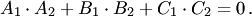
40.Условие ортогональности 2-х плоскостей.
две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 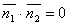или .

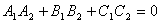Таким образом, .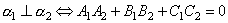
41.Задача о вычислении угла, образованного пересекающимися плоскостями

Две пересекающиеся плоскости образуют две пары смежных углов. Меньший из смежных углов называется углом между плоскостями.

Пусть пересекающиеся плоскости заданны следующими уравнениям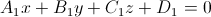и:

и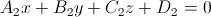

тогда угол между плоскостями вычисляется по следующей формуле:

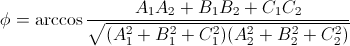
42.Векторно-параметрическое уравнение прямой в пространстве.
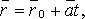где 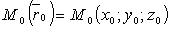- фиксированная точка, лежащая на прямой; 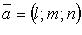- направляющий вектор.

В координатах (параметрические уравнения):

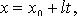
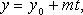
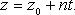
43.Каноническое уравнение прямой в пространстве.

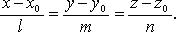
44.Векторное уравнение прямой в пространстве.
;

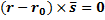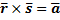
Матрицы. Виды матриц.

Свойства умножения матриц

Минор порядка к

Рассмотрим матрицу A:

Вычеркнем из матрицы k строк с номерами i1, i2, ..., ik и k столбцов, с номерами j1, j2, ..., jk.

Элементы, расположенные на пересечении вычеркнутых строк, образуют определиитель,

который называется минором порядка k. Его обозначают Mk:

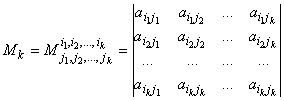
Обратная матрица. Опр.

Квадратная матрица, определитель которой отличен от нуля, имеет обратную матрицу и притом только одну

A*- матрица,сост. из алг.дополнения к элеметам А.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

:

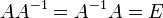
68) Условия существования и единственности обратной матрицы.

Единственность обратной матрицы докажем от противного. Пусть кроме матрицы 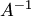существует еще одна обратная матрица 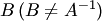такая, что 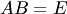. Умножая обе части этого равенства слева на матрицу 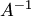, получаем 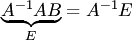. Отсюда 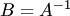, что противоречит предположению 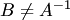. Следовательно, обратная матрица единственная.

Ранг матрицы. Опр.

Теорема о базисном миноре

Любой столбец матрицы А может быть предст. в виде лин.комбинации базисных столбцов (тех, кот. пересекают базисный минор)

Теорема Крамера

L- опред.А Li – получен из L заменой i-столбца на столбец свободных членов

Т. Кронекера- Капелли

Многочлены. Т. Базу

87)

Формула Эйлера

Векторы. Операции, свойства

Операции: 1)сложение (правило цепочки, параллелограмма, параллелепипеда)

1) вычитание –не является отдельной операцией,это всего лишь вид сложения,Герман)

3) умн. на число

Опр. линейной зависимости векторов

Система векторов 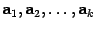называется линейно зависимой, если существует такой набор коэффициентов 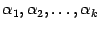, из которых хотя бы один отличен от нуля, что