Расчёт балки методом конечных разностей

Для заданной стальной балки переменного сечения (рис. 1) требуется:

1. определить кривую изогнутой оси;

2. при заданных нормативных нагрузках построить эпюру изгибающих моментов;

3. проверить жёсткость и прочность из расчётов по предельным состояниям.

Исходные данные

Шифр	№ двут.	l, м	q0, кН/м	q1, кН/м	М, кНм	R, МПа	gс	gf	[f / l]
31-6							0,95	1,1	1/200

Здесь l – длина пролета, q₁, q₂ – параметры распределенной нагрузки, описываемой по формуле

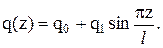
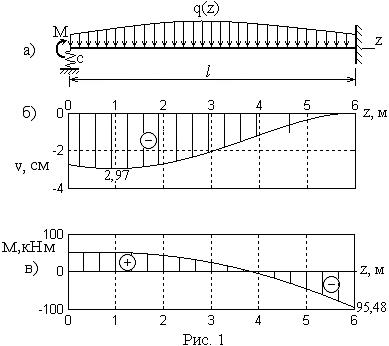
Расчетная схемаРешение

Изогнутая ось балки описывается дифференциальным уравнением четвёртого порядка

.

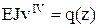Преобразуем его к более удобному виду

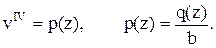(1)

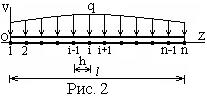
Область непрерывного изменения аргумента 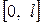заменим областью дискретного изменения (рис. 2)

.

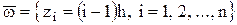Множество точек с номерами 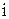называется сеткой, а сами точки узлами сетки. Вместо функции непрерывного аргумента 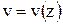будет отыскиваться сеточная функция .

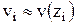К уравнению (1) присоединяются граничные условия. На левом конце балки упругая опора на пружине. Поэтому изгибающий момент в сечении равен приложенному моменту, а поперечная сила и упругая сила пружины уравновешены

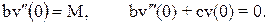(2)

На правом конце балки - заделка. Поэтому прогиб и угол поворота сечения равны нулю

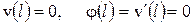. (3)

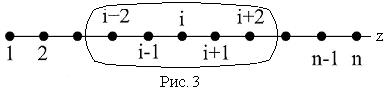
Производные и значения функции v в задаче (1) – (3) заменим конечноразностными соотношениями и значениями дискретной функции на пятиточечном шаблоне сетки (рис. 3):

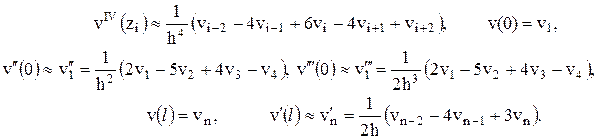(4)

Подстановка (4) в задачу (1) – (3) и элементарные преобразования приводят к конечноразностной схеме

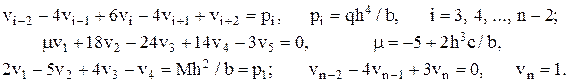
Запишем её как систему алгебраических уравнений относительно вектора 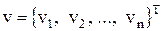в матрично-векторной форме

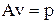, (5)

где

A = ,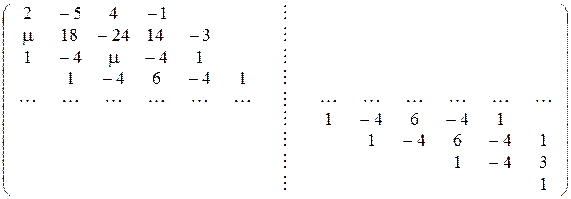

.

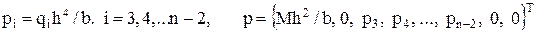Нулевые элементы матрицы не показаны, значок 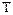в индексе соответствует операции транспонирования вектора.

Система уравнений (5) решается на компьютере с помощью подпрограммы вычислительного комплекса MATLAB, в результате чего становится известным вектор v.

Вычисления, проведенные на компьютере по данному алгоритму, показаны в виде кривой изогнутой оси на рис. 1б. Наибольший прогиб

|v|_max = 2,97 см.

Условие жёсткости имеет вид

.

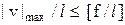Здесь в правой части требуемое по нормам отношение стрелы прогиба к длине балки, заданное условием задачи. Оно равно

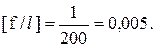
Вычислим левую часть отношения

.

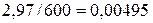Очевидно, что условие жесткости балки обеспечено.

Далее с помощью конечноразностных замен производных вычисляются изгибающие моменты по формуле

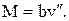
В переводе на конечноразностное представление она принимает вид во внутрисеточных узлах

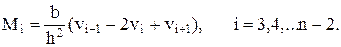(6)

На левом конце в точках i = 1, 2 изгибающий момент представляется в виде

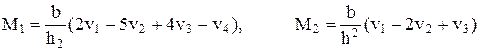. (7)

Аналогично на правом конце

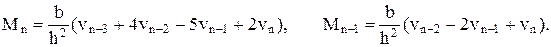(8)

Эпюра изгибающих моментов, построенная по (6) – (8) показана на рис. 1в. Наибольшее значение моментов от заданных нормативных нагрузок будет

|M|_max = 95,48 кНм.

Максимальное нормативное напряжение в этом сечении из расчета по второй группе предельных состояний будет

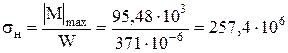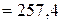Па МПа.

Расчетное напряжение получим путем умножения на заданный коэффициент надежности по нагрузкам

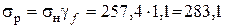МПа.

Условие прочности

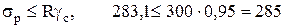МПа.

Прочность балки обеспечена

Листинг компьютерной программы на языке MATLAB.

% Балка. Cтатическая задача. 19.08.14

% Перемещения балки постоянного сечения.

% Метод конечных разностей, 5-титочечный шаблон

% Общая постановка задачи:

% v''''(z) = p, p(z)=q(z)/b b=EJ (1)

% Левый конец bv'''(0)+cv(0)=0, v''(0)=M

% Правый конец v'(l)=0, v(l)=0

% На балку действуют неравномерная поперечная нагрузка

% q(z)=q0+q1*sin(pi*z/l),

% направленная вниз, и сосредоточенный момент на левом конце

% Уравнение (1) и граничные условия приводится к

% алгебраической системе уравнений

% A v = p,

% которая решается с помощью данной подпрограммы MATLAB-а

clear; % disp('___________________');

% ИСХОДНЫЕ ДАННЫЕ:

l=6; E=210e+09; c=200000; J=5010e-08; W=371e-06; n=1001;

M=50000; q0=-8000; q1=-3000;

v=zeros(1,n); A=zeros(n,n); p=zeros(1,n); q=zeros(1,n);

b=E*J; h=l/(n-1); z=[0 : h : l];

mu=-5+2*c*h^3/b; q=q0+q1*sin(pi*z/l);

% Метод конечных разностей.

% Формирование матрицы А и вектора p

% Граничные условия

% Левый конец

A(1,1)=2; A(1,2)=-5; A(1,3)=4; A(1,4)=-1; p(1)=M*h^2/b;

A(2,1)=mu; A(2,2)=18; A(2,3)=-24; A(2,4)=14; A(2,5)=-3;

% Правый конец

A(n-1,n-2)=1; A(n-1,n-1)=-4; A(n-1,n)=3;

A(n,n)=1;

% Основное уравнение во внутренних узлах сетки

for i=3:n-2;

A(i,i-2)=1; A(i,i-1)=-4; A(i,i)=6; A(i,i+1)=-4; A(i,i+2)=1;

p(i)=q(i)*h^4/b;

end;

% Решение системы уравнений

v=A\p';

% Определение изгибающих моментов

% На левом конце

bh=b/h^2; m(1)=bh*(2*v(1)-5*v(2)+4*v(3)-v(4));

m(2)=bh*(v(1)-2*v(2)+v(3));

% В регулярных точках

for i=3:n-2;

m(i)=bh*(v(i-1)-2*v(i)+v(i+1));

end;

% На правом конце

m(n)=bh*(-v(n-3)+4*v(n-2)-5*v(n-1)+2*v(n));

m(n-1)=bh*(v(n-2)-2*v(n-1)+v(n));

% В Ы В О Д Г Р А Ф И К О В z - v, z - M Н А Э К Р А Н

plot (z, v*100, 'k','LineWidth',1), grid on;

xlabel('z,м'); ylabel('v, cм');

figure

plot (z, m/1000, 'k','LineWidth',1), grid on;

xlabel('z,м'); ylabel('M, кНм');

ВАРИАНТЫ ЗАДАНИЙ

Второе число шифра	№ дву- тавра.	l, м	q0, кН/м	q1, кН/м	М, кНм	R, МПа	gс	gf	[f / l]
		6,0					0,9	1,2	1/300
		6,2					0,95	1,3	1/200
		5,9					1,0	1,1	1/300
		5,6					0,9	1,2	1/200
		6,0					1,0	1,3	1/300

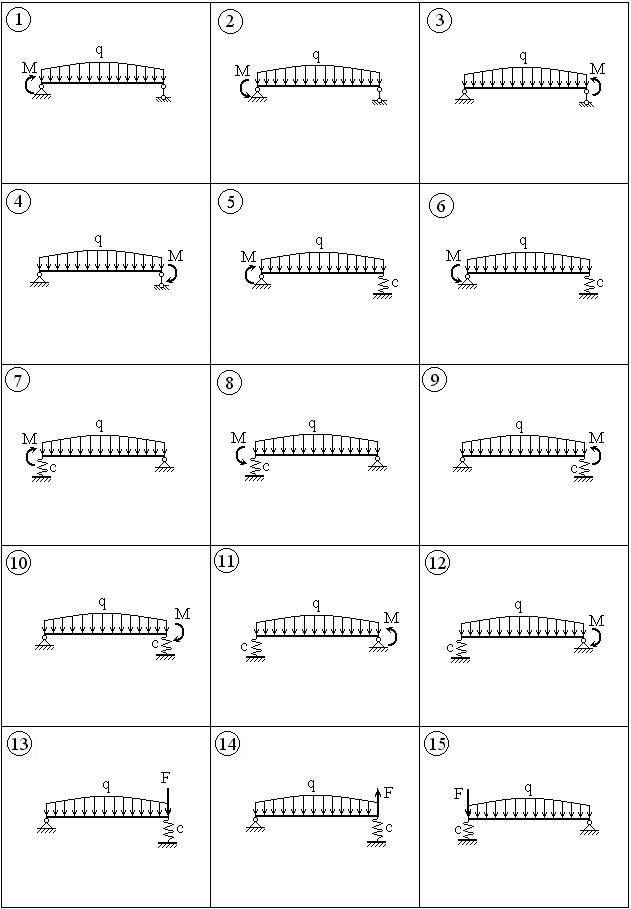
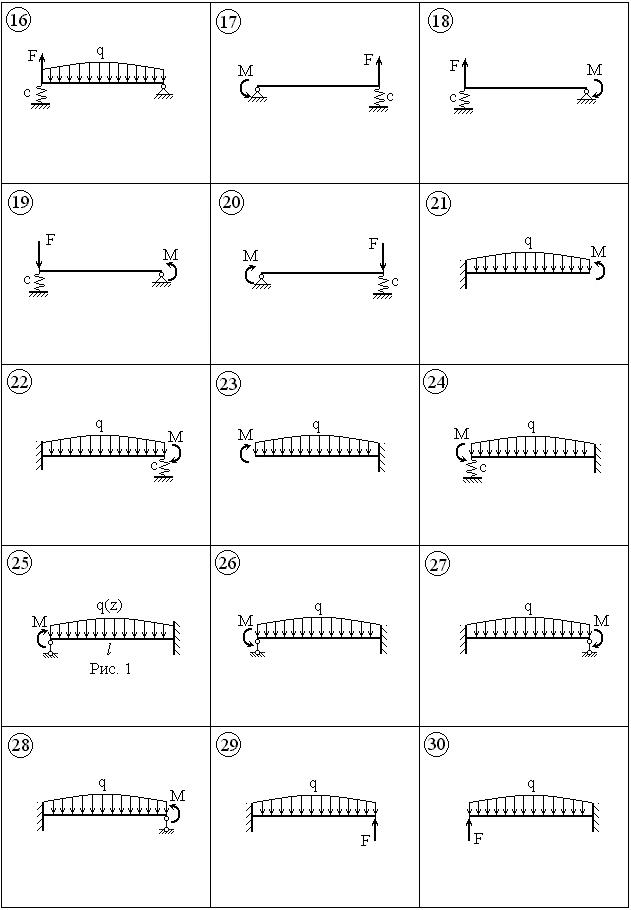
Задача 7