Примеры расчета пластинок методом конечных разностей

Для расчета МКР конкретной пластинки необходимо задать:

1) схему закрепления пластинки на контуре;

2) схему нагружения пластинки;

3) соотношение сторон пластинки а / b;

4) величину коэффициента Пуассона материала пластинки v ;

5) число N равномерного деления стороны контура прямоугольной пла­стинки конечно-разностной сеткой.

Если расчет пластинки производится в размерном виде, то дополни­тельно необходимо указать:

6) величину габарита пластинки по оси ОХ «а» (м);

7) величину модуля упругости материала пластинки Е (Па);

8) толщину пластинки h (м).

В дальнейшем будем указывать размер для сетки линий в области S, занимаемой пластинкой, в виде N×N, имея в виду весь план объекта. При этом шаг сетки будет равен а / N по оси х и b /N по оси у, где ах Ъ — раз­меры пластинки в плане (рис. 8).

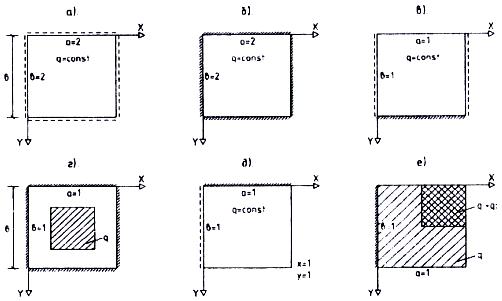
рис.2

Рассмотрим пластинку, изображенную на рис. 8 а, имеющую квадрат­ный план 2×2 (м), шарнирно-опертую по контуру, находящуюся под дей­ствием равномерно распределенной нагрузки q= const при значении коэф­фициента Пуассона материала v=0,3.

Конечно-разностный аналог дифференциального уравнения равнове­сия элемента пластинки Софи Жермен имеет вид:

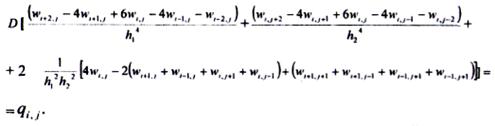(34)

Конечно-разностные аналоги граничных условий на сторонах пла­стинки будут:

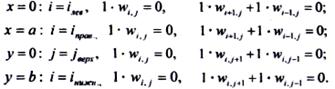(35)

Конечно-разностные аналоги условий в углах пластинки будут:

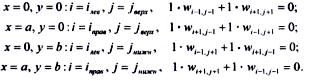(36)

При составлении приведенной в приложении к указаниям программы расчета пластинки МКР нумерация конечно-элементных узлов была сле­дующей. Первым узлом являлся левый верхний узел сетки во вторых за­контурных рядах по x и по y с координатами x=-2*h₁, y=-2*h₂. Так как значение прогиба «•, в данном узле не входит в формулы, то записываем:

.

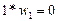Для второго законтурного узла с координатами x=-2*h₁, y=-h₂ зна­чение прогиба 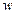, также не входит в формулы, поэтому записываем:

.

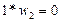Узлы с номерами i= 3,4,...,(im-2) расположены во втором законтурном ряду напротив узлов на стороне пластинки х = 0 и по правилу обратной симметрии для шарнирно-опертого края уравнения для них будут:

, , ,

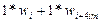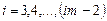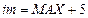где МАХ=8, 16, 32, 64 - указатель числа N равномерного деления стороны контура прямоугольной пластинки конечно-разностной сеткой.

Далее записываем для узлов i= iт-1, iт уравнения 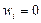после че­го записаны все уравнения для второго левого законтурного ряда узлов.

Для узлов первого законтурного ряда с номерами i= im + 1,..., 2*im с учетом шарнирного опирания сторон пластинки записываются уравнения:

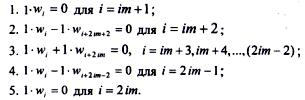
Для узлов ряда х = 0 с номерами i= 2iт +1,..., 3iт записываем урав­нения:

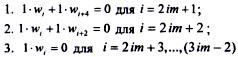- прогибы на шарнирно-опертой стороне

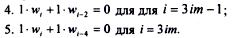
Наконец, для узлов четвертого слева вертикального ряда х = h, с но­мерами i= Зim +1,..., 4im записываем уравнения:

Такие же уравнения составляются для вертикальных рядов х = 2h₁, 3h₁ ,...,а – h₁, например, при значении МАХ=8 вертикальных рядов с записью в центральных узлах уравнения (34) будет всего семь.

Далее в порядке, обратном порядку для вертикальных рядов слева, за­писываются уравнения для рядов с номерами iт - 2,iт - 1,iт , что в итоге дает систему IM *IM разрешающих конечно-разностных уравнений.

Отметим, что при изменении порядка следования конечно-разностных уравнений на главной диагонали матрицы А системы 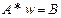линейных алгебраических уравнений МКР может появиться коэффициент, равный нулю, что автоматически сделает систему 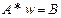неразрешимой.

Отметим также, что подготовка исходных данных для приведенной в приложении к указаниям универсальной программы расчета пластинки МКР состоит в задании следующих входных параметров:

1 ) NXNА - указатель опирания пластинки по стороне х = 0: NXNА = 1 (шарнирное опирание в рассматриваемом примере с рис. 8 а);

2) NXКО - указатель опирания пластинки по стороне х = а: NXКО = 1 (шарнирное опирание в рассматриваемом примере с рис. 8 а);

3) NYNА - указатель опирания пластинки по стороне у = 0: NYNА=1 (шарнирное опирание в рассматриваемом примере с рис. 8 а);

4) НYКО - указатель опирания пластинки по стороне у = b: НYКО=1 (шарнирное опирание в рассматриваемом примере с рис. 8 а);

5) RAZMER - габарит пластинки по оси x (м) (RAZMER = 2);

6) АВ = а/b - отношение сторон пластинки в плане (АВ = 1);

7) qYKA - указатель типа распределения поперечной нагрузки (для рас­сматриваемой равномерно распределенной нагрузки qYКА = 1);

8) РYАS - величину коэффициента Пуассона материала пластинки -вводим РYАS = 0,3;

9) МАХ- указатель числа ТУ для равномерного деления стороны конту­ра прямоугольной пластинки конечно-разностной сеткой: последовательно вводим МАХ = 8, 16, 32, 64.

При решении задачи в безразмерном виде программа задает величину интенсивности поперечной нагрузки Q = 1.

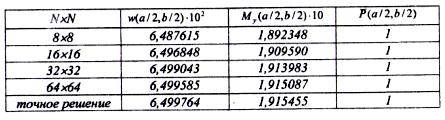
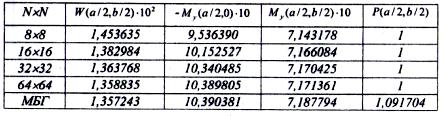
В табл. 1 приведены результаты расчета МКР пластинки (рис. 8 а). Прогибы iv (табл.1 и в дальнейшем) приводятся с точностью до множите­ля qa⁴/D , моменты - с точностью до множителя qa², где q - величина поперечной нагрузки. Величина Р соответствует решению обратной задачи о нахождении величины интенсивности нагрузки q_i,j, исходя из полученных значений прогибов в узлах сетки 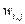, которые для этого подставля­ются в левую часть уравнения (34). За точное в табл. 1 принято решение в двойных тригонометрических рядах:

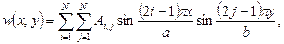(37)

в приближении N = 111, которое не уточняется приближениями с N > 111 по всем значащим цифрам.

Установлено, что невязки по нагрузке в узлах сетки в МКР отсутст­вуют, и уже на сетке 8×8 отличие от точного решения по наибольшим про­гибам 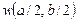составляет менее 0,2%, а по наибольшим изгибающим моментам 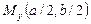1,2%, что соответствует высокой точности решения.

Решение же на сетке 32×32, когда в н» получается четыре, а в М_h три верные цифры, что соответствует весьма высокой точности решения зада­чи, занимает весьма незначительное время ПЭВМ, что свидетельствует о высокой экономичности МКР.

Таблица 1

В табл. 2 приведены результаты для аналогичной пластинки, защем­ленной на контуре (рис. 8 б). В качестве эталонного взято решение по ме­тоду Бубнова-Галеркина в приближении с 64 членами ряда разложения функции прогиба 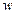в виде ортонормированных полиномов, методика по­строения которых изложена в [5].

Таблица 2

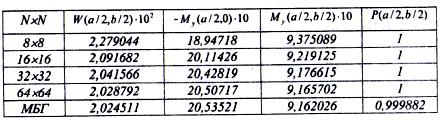
Ввиду того, что при защемлении краев пластинки кривизны ее изо­гнутой срединной поверхности двузначны, сходимость решения по МКР замедляется по сравнению со случаем шарнирного закрепления сторон. Однако уже при сетке 16×16 прогиб в центре отличается от «эталонного» решения лишь на 3,3%, изгибающий момент в центре - на 0,6% и на кон­туре - на 2,0%, что соответствует хорошей точности решения задачи. Точ­ность решения задачи МКР на сетке 32×32 существенно выше, а затраты времени ПЭВМ весьма малы.

Заметим, что в обоих примерах шаг сетки каждый раз уменьшался в 2 раза, что определяется известным принципом Рунге исследования сходи­мости приближенных решений [7].

Этот же принцип положен в основу исследования сходимости реше­ния МКР для равномерно нагруженной пластинки с размерами 1×1 (м) со свободной стороной при у = 0, защемленной стороной при у = Ь , шарнирно-опертыми сторонами при х = 0 и при х = а, приведенной на рис.8 в.

В табл. 3 даны результаты расчетов по МКР, сопоставляемые с из­вестным решением [4].

Таблица 3

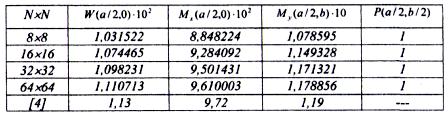
Результаты табл. 3 свидетельствуют об устойчивой и достаточно бы­строй сходимости решения по МКР, причем для сетки 32×32 отличие ре­зультатов от данных [4] составляет: по наибольшему прогибу 2,9%, по ве­личине M_x(a/2,b) 2,3% и по наибольшему изгибающему моменту M_y(a/2,0) 1,6%, что свидетельствует о высокой точности решения МКР при использовании сетки 32×32.

Заметим, что решение на сетке 8×8 (табл. 3) имеет посредственную точность. Например, по величине W(а/2,b) имеем погрешность в 9,54%, по М_х(а/2,b) 9,85%, по M_y(a/2,0) 10,33%. Однако уже данное при­ближение МКР качественно верно описывает изменение всех параметров напряженно-деформированного состояния пластинки по всему ее полю.

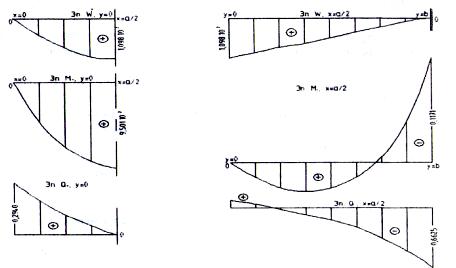
Рис.9

Отметим также, что решение МКР на сетке 64×64 несущественно уточняет результаты при сетке МКР 32×32, но требует для своей реализа­ции неизмеримо больше времени счета ПЭВМ.

На рис. 9 приведены эпюры прогиба w изгибающих моментов М_x,М_у и поперечных сил Q_x, Q_y в сечениях х = а/2, у = b/2 данной пла­стинки, полученные МКР на сетке 32×32.

Если рассматривать пример локального нагружения пластинки, то следует ожидать уменьшения скорости сходимости МКР, так как это при­суще всем без исключения методам расчета. В табл. 4 приведены резуль­таты для защемленной на контуре пластинки, нагруженной по 25% ее пло­щади в центральной части, причем а = b = 2(м), v = 0,3 (рис. 8 г). Резуль­таты по МКР сравниваются с решением по методу Бубнова-Галеркина в приближении с 64 варьируемыми параметрами в ряде разложения функции прогиба по ортонормированным полиномам [5].

Таблица 4

Отметим, что и для данного случая решение по МКР на сетке 32×32 дает значения параметров напряженно-деформированного состояния пла­стинки, весьма близкие к решению по методу Бубнова-Галеркина - расхо­ждение по величине М_у(а/2,0) составляет лишь 0,48%.

При использовании вариационных методов расчета затруднения воз­никают при наличии у пластинки смежных свободных от закреплений сто­рон. Проводим с использованием МКР расчет пластинки, приведенной на рис. 8 д, имеющей свободные стороны при х = а и у = Ь.

В табл. 5 приведены результаты расчета МКР пластинки с размерами 1×1 (м), находящейся под действием равномерно распределенной нагруз­ки q=const=1, коэффициент Пуассона материала пластинки v= 0,3.

В табл. б приведены данные для аналогичной пластинки при наличии в ее правом нижнем углу точечной шарнирной опоры (рис. 8 д). Заметим, что при этом конечно-разностный аналог (34) уравнения равновесия для узла х =а, у =b:i= i_прае, j = j_нижн заменялся уравнением w_{iправ.,jнижн.}=0.

Таблица 5

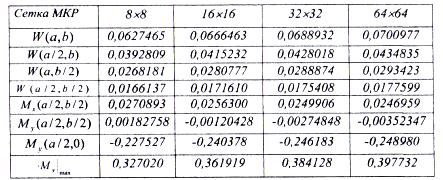
Примечание. Свободный угол пластинки х = а, у = b.

Таблица 6

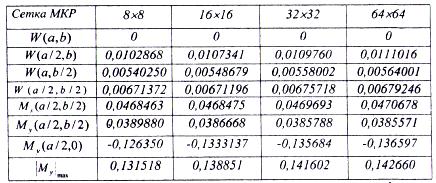
Примечание. Точечная шарнирная опора в углу пластинки х = а, у = b.

Результаты табл. 5, 6 свидетельствуют об устойчивой и достаточно быстрой сходимости решения по МКР, причем результаты для сетки 32×32 весьма близки к данным на сетке 64×64.

Отметим по результатам табл. 5, что величина изгибающего момента M_y(a/2,b/2) для данной задачи является малой по сравнению с величи­ной M_x(a/2,b/2), поэтому можно удовлетвориться констатацией факта мо­нотонности изменения М_у(а/2,b/2) с уменьшением шага сетки.

Кстати, из данных табл. 6 следует, что при введении точечной шар­нирной опоры в угол пластинки х = а, у = b распределение параметров напряженно-деформированного состояния (НДС) пластинки по ее полю претерпевает качественное изменение. Например, М_у (а /2, b/2) перестает быть малой величиной по сравнению с М_x(а/2,b/2). Кроме того, сходи­мость МКР по величине М_у(а/2,b/2) является очень быстрой – данные приближения с сеткой 8×8 отличаются от данных при сетке 32×32 всего лишь на 1,1%.

Сопоставление данных табл. 5 и 6 свидетельствует, что при введении упомянутой опоры прогибы в характерных точках пластины резко умень­шаются: величина W(а/2,b) убывает в 3,92 раза, величина W(а,b/2) - в 4,32раза, величина W (а / 2,b / 2) - в 2,61 раза.

Также убывает в 1,82 раза величина M_y(a/2,0), а вот значения изги­бающих моментов в центре пластинки возрастают за счет увеличения кри­визны изогнутой срединной поверхности, например, величина M_x(a/2,b/2) становится больше в 1,91 раза. Однако наибольший по абсолютной вели­чине момент 'М^ уменьшается в 2,77 раза, то есть введение точечной шарнирной опоры в угол пластинки х = а, у = b существенно уменьшает как прогибы, так и наибольший изгибающий момент в пластинке.

Заметим, что введение точечных шарнирных опор возможно в любых узлах конечно-разностной сетки МКР, что дает возможность вариантного проектирования пластинок. В табл. 7 приведены данные расчетов для пла­стинки с размерами а = b= 21 (м) для случая наличия точечных шарнир­ных опор в углах пластинки и свободных от закреплений сторон контура.

Таблица 7

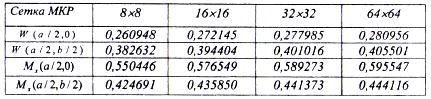
Результаты табл. 7 свидетельствуют об устойчивой и достаточно бы­строй сходимости решения по МКР, причем результаты для сетки 32×32 весьма близки к данным на сетке 64×64. Отметим, что по результатам вы­числений МКР на ПЭВМ на дисплей для заданных сечений пластинки вы­водятся величины параметров НДС пластинок, а именно W, M_x, M_y, H, Q_x, Q_y, что дает возможность построить эпюры данных функций.

Рассмотрим в заключение расчет МКР в размерном виде прямоуголь­ной в плане пластинки, защемленной на стороне контура х = 0 и имеющей три свободные стороны контура соответственно при х = а, у = 0, у = b (рис. 8 е).

Поперечная нагрузка q состоит суммы постоянной по поверхности на­грузки q₁=0.4*10⁴ (Па) и нагрузки q₂ =0.8*10⁴ (Па), действующей на верхнюю правую четверть пластинки (рис. 8 е). Задаем величины входных параметров задачи: а = 3(м), а/b = 0,75, v= 0,15, Е = 2,1*10¹⁰ (Па), h=0,2 (м).

В табл. 8 приведены данные исследования сходимости решений МКР для обсуждаемой пластинки.

Таблица 8

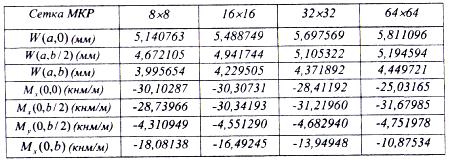
Анализ данных табл. 8 свидетельствуют об устойчивой и достаточно быстрой сходимости решения по МКР. Кроме того, установлено, что вели­чина момента M_x(0,b) при сгущении сетки прогрессивно убывает, величи­на M_x(0,b/2)=M_max возрастает, а отношение M_max/ M_x(0,b) составляет 2,91. Отношение моментов М_х(0,0)/М_x(0,b)=25,032/10,875=2,30, а соотноше­ние прогибов пластинки в крайних верхней и нижней точке при значении х = 3(м) составляет 1,306.

Если же провести расчет балок с габаритами h = b= 0,2 (м), выре­занных из данной пластинки соответственно при у = 0,1 (м) и у = 3,9 (м), то величины характерных изгибающих моментов будут: М_х(0,0) =-45 (кнм/м), M_x(0,b) =-18 (кнм/м), то есть увеличение по сравнению с моментами в пластинке происходит соответственно в 1,8 и 1,66 раза.

Кроме того, прогибы в данных балках соответственно в 39,18/5,811=6,74 и 14,47/4,4497=3,25 раза превышают прогибы в пластин­ке, а соотношение прогибов на концах балок равно 0,03918/0,01447=2,708, что в 2,07 раза превышает данное соотношение для пластинки.

Все отмеченные выше факты подтверждают настоятельную необхо­димость расчета пластинок, а не вырезанных из них балок - лишь данный подход позволяет учесть особенности работы пластинок при сопоставимых габаритах а и b и добиться существенной экономии материала.

Подчеркнем в заключение, что рассмотрение всех приведенных при­меров расчета пластинок приводит к однозначному выводу о хорошей схо­димости МКР для пластинок на прямоугольном плане при любых условиях закрепления и нагружения.