Метод конечных разностей

Самым распространенным численными методом решения краевых задач для ДУ является метод конечных разностей.

Рассмотрим краевую задачу

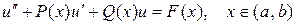(1)

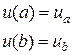(2)

или в операторной форме

,

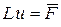где

, .

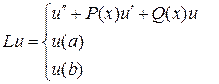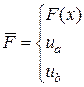Здесь 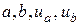– заданные числа, 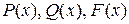– заданные функции. При этом, исходные данные задачи должны быть такие, чтобы задача имела единственное решение – функцию 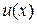непрерывную и дважды дифференцируемую на 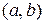(рис. 1).

Первый шаг алгоритма МКР состоит в том, что отрезок 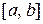разбивается точками (рис. 6) с координатами

,

.

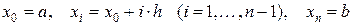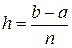Совокупность точек 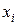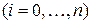называется сеткой, сами точки – узлами, параметр 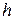называется шагом по сетке. Точки 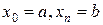называют граничными узлами, а точки 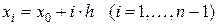– внутренними узлами сетки.

Будем искать не решение 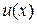исходной задачи (1) – (2), а таблицу 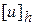значений этого решения в узлах 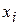сетки. Такая функция называется сеточной. Значения искомой сеточной функции 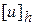в узлах 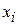будем обозначать .

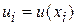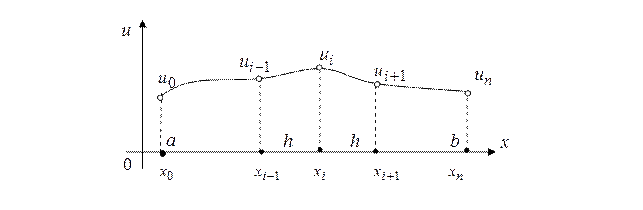Рис. 1. Дискретная модель задачи

При переходе от непрерывного описания задачи к дискретному исходное уравнение (1) мы должны заменить системой уравнений, записанных к каждой точке введенной сетки. Но сначала надо решить вопрос о вычислении производных первого и второго порядка сеточной функции.

Следующий шаг алгоритма МКР – замена дифференциальных операторов конечно-разностными соотношениями.

Рассмотрим функцию одной переменной 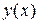и выведем для неё формулы численного дифференцирования. Согласно определению производная функции 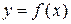в точке 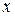есть предел отношения приращения функции 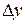к приращению аргумента 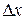при стремлении 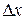к нулю

.

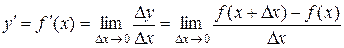Пусть имеется табличная функция (таблица значений функции 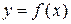) с шагом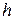

		………………..
		………………..

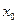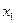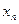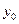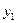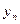В этом случае производную в узле таблицы можно приближенно можно найти по формуле

.

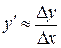Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разносте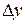й и 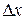. В зависимости от способа вычисления конечных разностей получают разные формулы для вычисления первой производной табличной функции. Предположим, что шаг таблицы (разность между соседними значениями аргументов) постоянный и равен 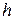. Запишем формулы вычисления первой производной в узле :

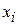с помощью правых конечных разностей , :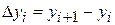

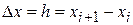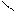
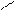
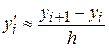
с помощью левых конечных разностей , :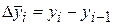

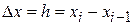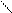
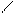
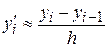
Из этих формул можно получить формулу вычисления производной с помощью центральных разностей , :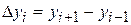

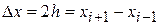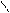
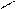
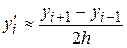
Используя аппроксимации первой производной, можно получить приближение старших производных. Например

.

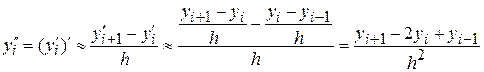Полученные формулы вычисления производных являются приближенными, так что имеет смысл рассмотреть величину

,

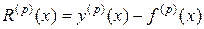которая характеризует отклонение приближенного значения производной от её истинного значения и называется погрешность аппроксимации производной 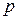-го порядка.

Если функция задана таблицей с шагом 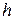, погрешность аппроксимации зависит от 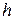, и её записывают в виде 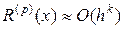(О большое от 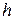). Показатель степени 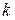называется порядком погрешности аппроксимации или порядком точности аппроксимации (при этом предполагается, что ).

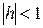Замечание. (о символе "О – большое").

Говорят, что функция 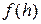приближает функцию 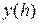с порядком 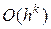, и записывают

,

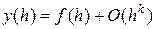если что существует константа 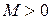и положительное число 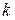, такие что

.

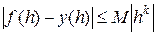Приведенные формулы численного дифференцирования имеют следующую точность:

.

.

. (*)

. (**)

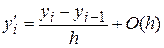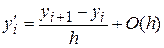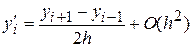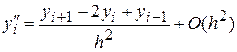Вернемся к задаче (1) – (2).

Запишем уравнение (1) для каждого внутреннего узла введенной сетки, используя формулы для аппроксимации производных центральными конечными разностями (*) и (**), а также обозначая 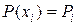, , 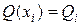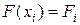в узлах сетки.

В результате приходим к системе линейных алгебраических уравнений относительно значений неизвестных функций в узлах

.

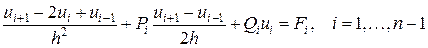Добавляем к этой системе условия в граничных узлах

,

.

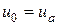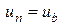После преобразования система примет вид:

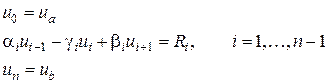(3)

где , , , , .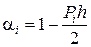

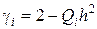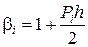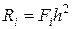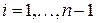Система метода конечных разностей (3) называется разностной схемой задачи (1) – (2). Третий шаг алгоритма МКР – решение СЛАУ (3).

Представим систему (3) в матричной форме

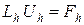. (4)

Решение задачи (4) – вектор 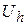размерностью 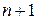. При этом возникает вопрос: является ли полученный вектор приближением к решению исходной задачи и если это так, то какова степень точности этого приближения. Таким образом, возникает задача анализа сходимости численного метода как критерия точности вычислительного процесса.

Разностная схема 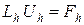сходиться к решению исходной задачи 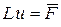, если имеет место сходимость по норме

,

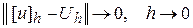где 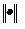– норма сеточной функции, а 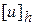– вектор узловых значений точного решения. Если, сверх того выполнено неравенство

,

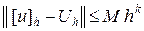где 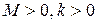– некоторые постоянные, то говорят, что имеет место сходимость порядка 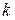относительно .

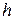В частном случае метод конечных разностей сходится к решению краевой задачи (1) – (2), если в дифференциальном уравнении 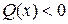для всех 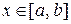, а в определяющем разностном уравнении .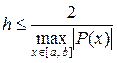