Метод конечных разностей для линейных дифференциальных уравнений второго порядка

Пусть x₀ = a, x_n = b, x_i = x₀ + ih (i = 1, 2, …, n – 1) – система равноотстоящих узлов с некоторым шагом h = (b – a)/n и

p_i = p(x_i), q_i = q(x_i), f_i = f(x_i).

Пусть y_i, 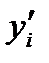, 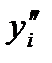– приближенные значения функции y(x) и ее производных , .

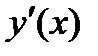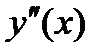Можно приближенно заменить в каждом внутреннем узле производные 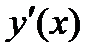, 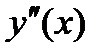конечно-разностными отношениями

.

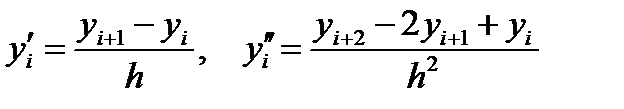(6.39)

На концах отрезка примем

.

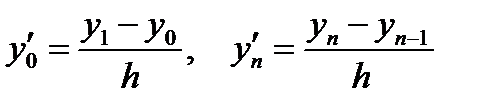(6.40)

Теперь можно приближенно заменить уравнение (6.37) и краевые условия (6.38) системой (n+1) уравнений с (n+1) неизвестными:

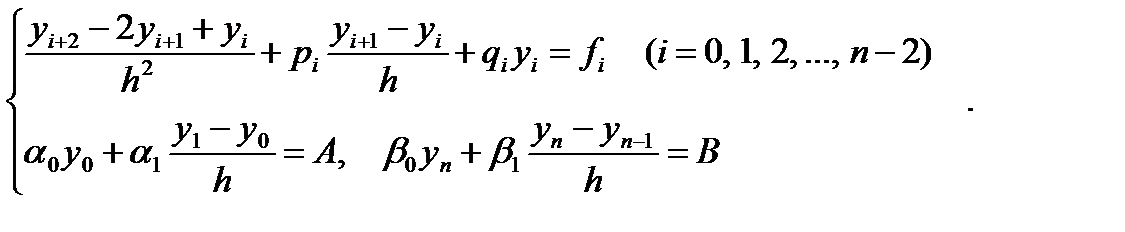(6.41)

Более точные формулы получаются при использовании центрально-разностных отношений:

.

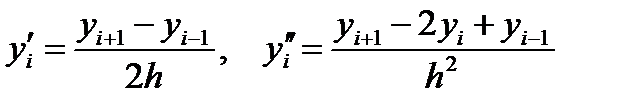(6.42)

Теперь вместо системы (6.41) получаем:

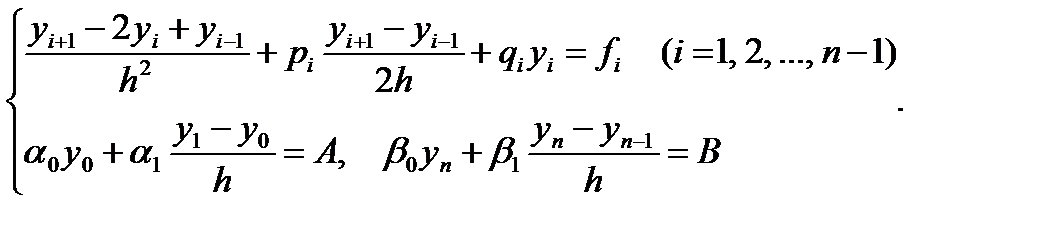(6.43)

Пример решения уже был рассмотрен.

Оценка погрешности

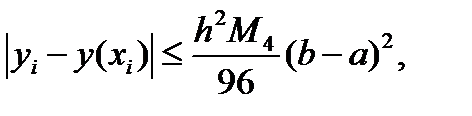(6.44)

где y(x_i) – значение точного решения при x = x_i, M₄ = max|y⁽⁴⁾(x)| .

Метод редукции к задаче Коши двухточечной краевой задачи

Рассмотрим на отрезке [a, b]граничную задачу для дифференциального уравнения

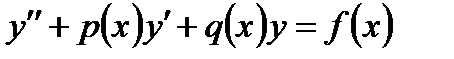(6.45)

с условиями

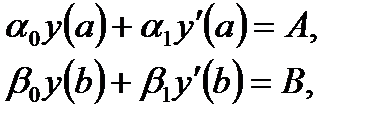(6.46)

где p(x), q(x), f(x) – непрерывные на отрезке [a, b] функции.

Решение уравнения (6.45), удовлетворяющее краевым условиям (6.46), будем искать в виде

,

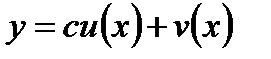(6.47)

где u = u(x) – решение соответствующего однородного уравнения

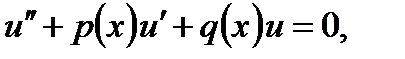(6.48)

а n = n(x) – частное решение неоднородного уравнения

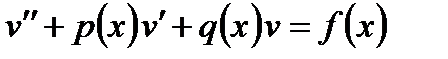(6.49)

Подставим (6.47) в первое условие граничной задачи (6.46), получим

.

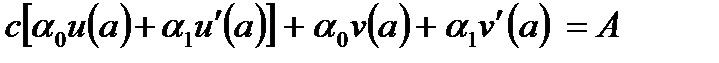(6.50)

Для того чтобы равенство (6.50) было справедливо при любом с, необходимо и достаточно, чтобы сомножитель 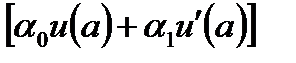= 0 и выполнялись следующие равенства:

.

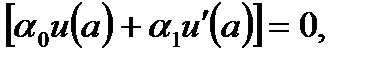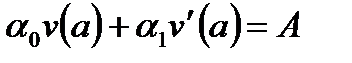(6.51)

Примем

,

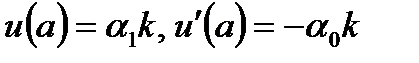(6.52)

где константа k отлична от нуля.

Если 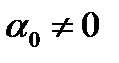, то

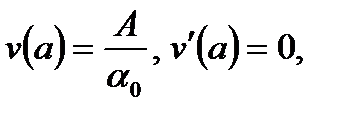(6.53)

если 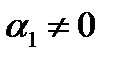, то

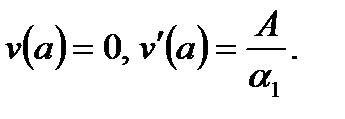(6.54)

Видно, что u = u(x) является решением задачи Коши для однородного уравнения (6.48), удовлетворяющим начальным условиям (6.52), а n = n(x) – решение задачи Коши для неоднородного уравнения (6.49), удовлетворяющее начальным условиям (6.53) или (6.54).

Теперь подставим (6.47) во второе условие граничной задачи (6.46) и выразим постоянную с

.

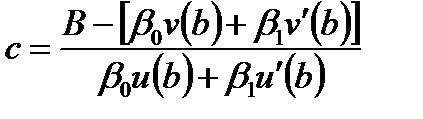(6.55)

При этом предполагается, что 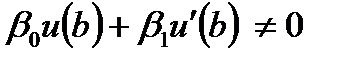. Если выполнено это условие, то краевая задача (6.45) - (6.46) имеет единственное решение, в противном случае она или совсем не имеет решений, или их бесчисленное множество.

Метод коллокации

Решение краевой задачи (6.45), (6.46) ищем в виде

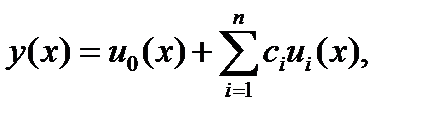(6.56)

где u_i(x)(i = 0, 1, 2, …, n) – линейно независимые ортогональные функции.

Обозначим

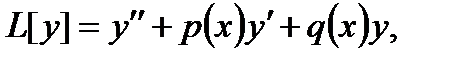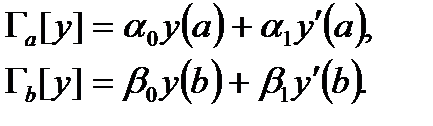(6.57)

Потребуем, чтобы невязка

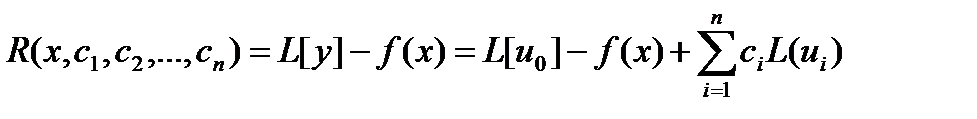(6.58)

обращалась в нуль на некоторой системе точек x₁, x₂, …, x_n отрезка [a, b].

Эти точки называются точками коллокации, их число должно равняться числу коэффициентов c_i в выражении (6.56).

Для определения c_i получаем систему уравнений

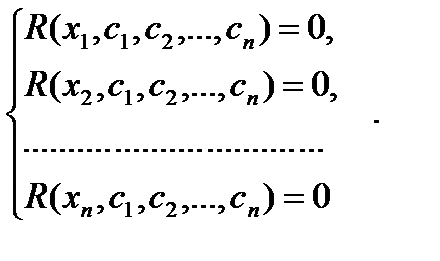(6.59)

Метод коллокации можно применить и для решения нелинейных уравнений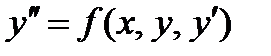
c линейными краевыми условиями.

При этом невязка имеет вид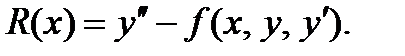

Система (6.59) будет системой нелинейных алгебраических уравнений относительно неизвестных c_i.

Пример

Методом коллокации найти приближенное решение уравнения

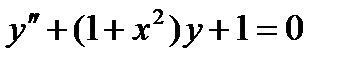
c краевыми условиями

y(–1) = y(1) = 0.

Выберем в качестве базисных функций u₀(x) = 0, u₁(x) = 1 – x², u₂(x) = x²(1– x²).

Краевые условия для них выполняются. Решение будем искать в виде

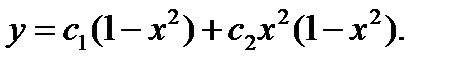
За точки коллокации возьмем x₀ = 0, x₁ = ½.

Составляем невязку R(x):

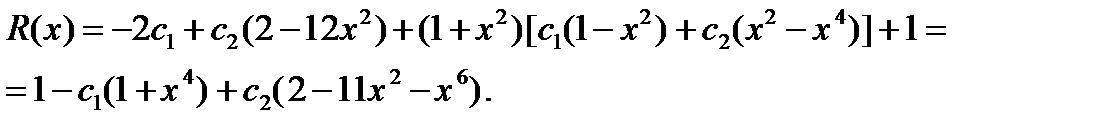
Подставив x₀ = 0, x₁ = ½,получаем систему

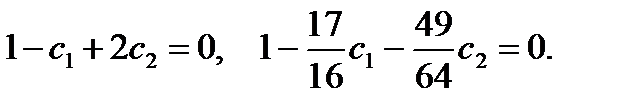
Отсюда находим c₁ = 0,957; c₂ = – 0,022.

Приближенное решение имеет вид

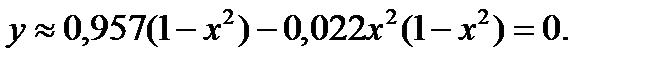
Тема 7

Метод конечных разностей
(метод сеток) численного решения дифференциальных уравнений

Метод сеток, или метод конечных разностей – один из самых распространенных методов численного решения уравнений с частными производными.

В основе – идея замены производных конечно-разностными отношениями.

Ограничимся случаем двух независимых переменных.

Пусть в плоскости xOy имеется некоторая область G с границей Г (рис. 7.1).

Рис. 7.1. Построение сетки

Построим два семейства параллельных прямых:

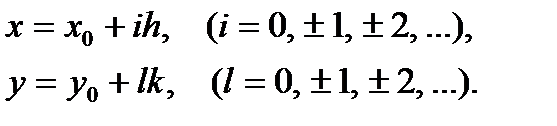
Точки пересечения прямых называют узлами.

Два узла называют соседними, если они удалены вдоль оси Ox или Oy на шаг сетки h или k соответственно.

Узлы, принадлежащие G + Г и расположенные вне этой области на расстоянии, меньшем, чем шаг от Г, называют внутренними.

Оставшиеся из выделенных – граничные.

Рассмотрим сначала разности в направлении x.

Разложим функцию u = u(x, y₀)в ряд Тейлора в окрестности точки x₀, y₀:

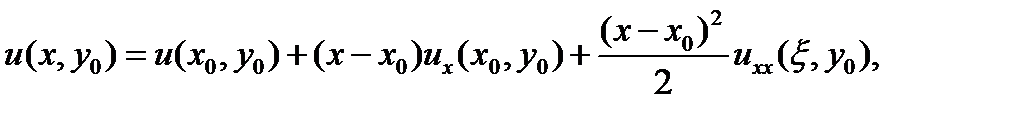
где x лежит между x и x₀.

Если положить x = x₀ + h, то можно получить следующее выражение

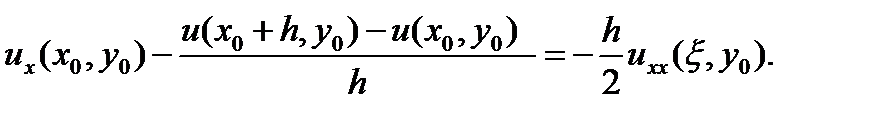
Т. е. если представить u_x с помощью

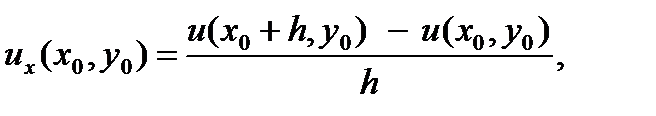(7.1)

то ошибка ограничения будет равна

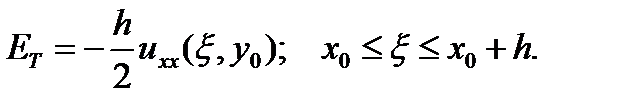
Равенство (7.1) получено с помощью подстановки x = x₀ + h,результат называется правой разностью.

Аналогично можно получить левую разность:

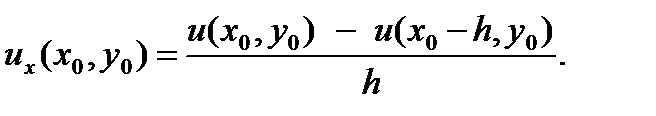(7.2)

Приближение для второй производной u_xx через правую разность:

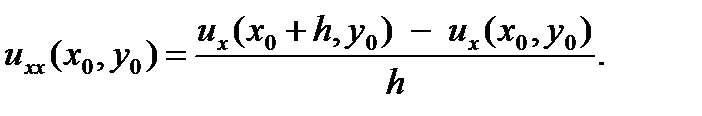(7.3)

Если в выражение (7.3) подставить правые разности для u_x, весь результат окажется «сдвинут» вправо. Для компенсации используем левые разности для u_x. Получим

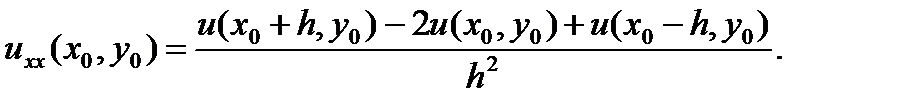(7.4)

Можно отметить симметрию полученной формулы относительно x₀, y₀.

Для определения ошибки ограничения вспомним, что

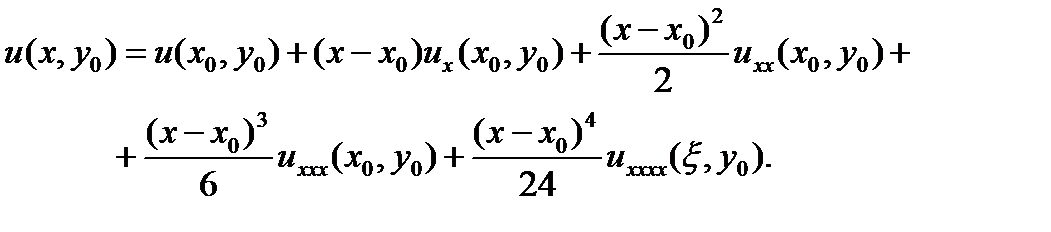
Положим теперь x = x₀ + h; x = x₀ – h и сложим два равенства. Получится, что ошибка ограничения равна

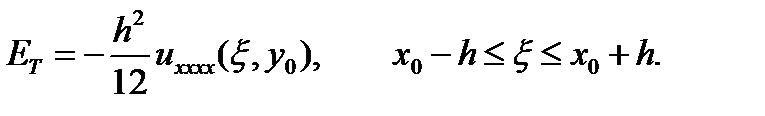
Аналогичный анализ проводится для производных в направлении y:

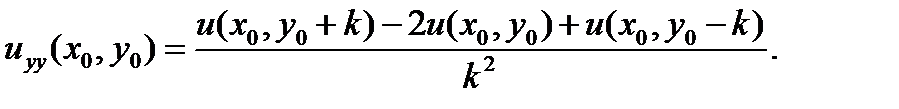(7.5)

Здесь k – величина шага по y.

Ошибка ограничения равна

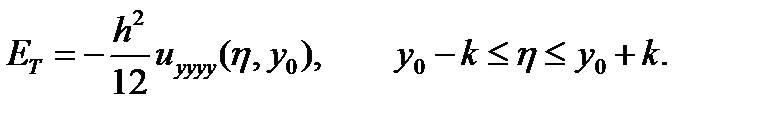
С использованием полученных выражений можно полностью переписать дифференциальное уравнение в частных производных и перейти к уравнению в конечных разностях.

Например, уравнение Лапласа

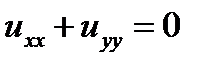
можно переписать в виде

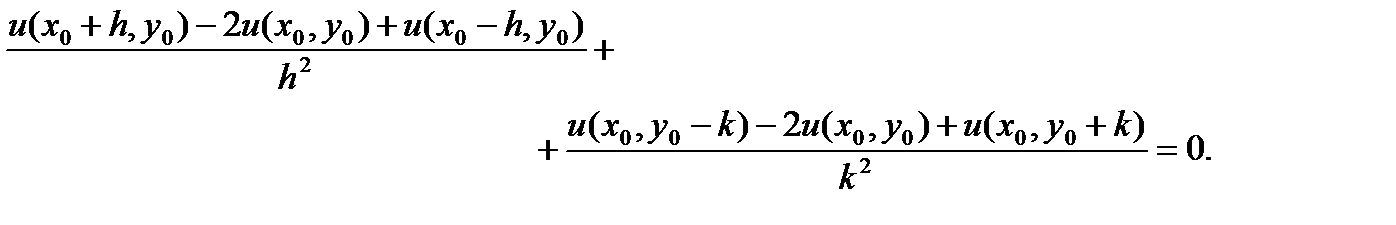
Тема 8

Решение дифференциальных уравнений в частных производных

8.0 ДУ в частных производных. Постановка задачи

Ограничимся линейными дифференциальными уравнениями второго порядка с двумя независимыми переменными.

Их можно представить в виде

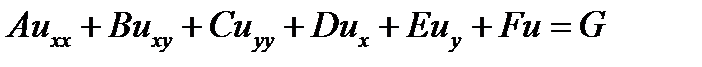(8.1)

Здесь A ¸ G – функциитолько независимых переменных x и y. Зависимой переменной является u.

В случае обыкновенных дифференциальных уравнений из семейства решений выбиралось нужное с помощью начального условия.

Теперь, поскольку независимых переменных 2, условия должны задаваться вдоль какой-либо кривой в плоскости xОy.

Условие может налагаться на функцию, ее производную, либо совместно.

Будет кривая замкнутой либо разомкнутой зависит от типа уравнения.

Обычно уравнения второго порядка подразделяют на три типа (см. (8.1)).

1. Уравнение называют эллиптическим, если B² – 4AC< 0.

2. Уравнение называют параболическим, если B² – 4AC = 0.

3. Уравнение называют гиперболическим, если B² – 4AC> 0.

Уравнение может принадлежать к нескольким типам в зависимости от коэффициентов. Уравнение

yu_xx + u_yy = 0

эллиптическое при y > 0, параболическое при y = 0 и гиперболическое при y < 0.

8.1 ДУ в частных производных. Эллиптические уравнения

Типичный пример задачи – расчет напряжений при кручении длинного цилиндрического стержня (рис. 8.1).

Обозначим через q угол кручения на единицу длины.

Единственными ненулевыми напряжениями сдвига являются t_x и t_y (индексы здесь не означают дифференцирование).

Рис. 8.1. К задаче о кручении стержня

Если определить функцию y через уравнения

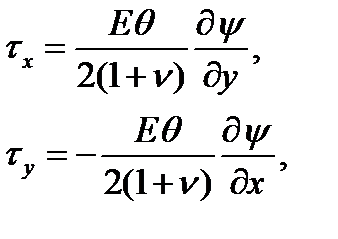
то функция y является решением уравнения

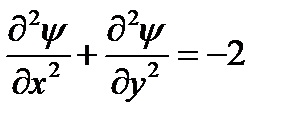(8.2)

внутри области R, а на границе области С 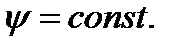Можно принять y = 0 на кривой С.

Уравнение (8.2) называют уравнением Пуассона.

Рассмотрим классическую задачу Дирихле

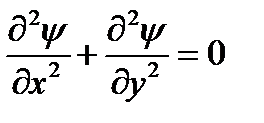(8.3)

в некоторой области R и на границе этой области (С):

.

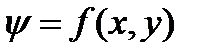(8.4)

Уравнение (8.3) – это уравнение Лапласа (частный случай уравнения Пуассона).

Для простоты рассмотрим случай, когда кривая С состоит из отрезков прямых, параллельных осям Ox и Oy. Рассмотрим прямоугольник шириной L и высотой H (рис. 8.2).

Рис. 8.2. Построение прямоугольной сетки

Введем шаги h = L/n и k = H/m. Получим (n – 1)(m – 1) пересечений. Обозначим

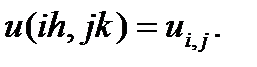
Аналогично запишем

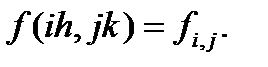
При этом граничное условие (8.4) можно записать в виде

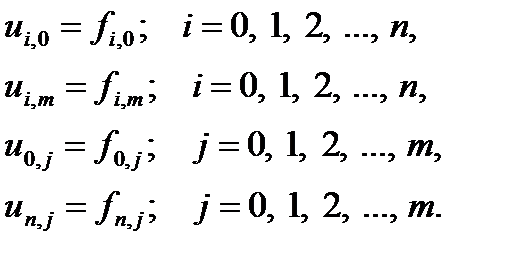(8.5)

Пусть теперь точка i, j будет точкой x₀, y₀ в выражениях (7.3) и (7.5).

Если обозначить l = k/h, то уравнение Лапласа (8.3) сведется к разностному уравнению вида

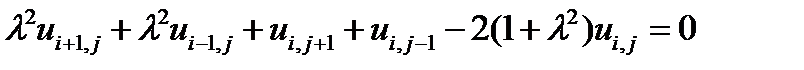(8.6)

для i =1, 2, 3, …, n – 1 и j = 1, 2, 3, …, m – 1.

При l = 1 u_i,j представляет собой среднее арифметическое из четырех соседних узлов.

Уравнение (8.6) можно представить схематически, начертив пять узлов разностного уравнения и обозначив около каждого из них соответствующий коэффициент.

Этот рисунок называется «трафаретом». «Трафарет» геометрически иллюстрирует разностную аппроксимацию дифференциального уравнения (рис. 8.3).

j + 1 j i i +1 +1 +1 + l2 – 2(1 + l2) j – 1 i – 1 + l2

Рис. 8.3. «Трафарет» для уравнения эллиптического типа

Имеем систему (m – 1)(n – 1) уравнений относительно (m + 1)(n + 1) неизвестных.

С помощью граничных условий (8.5) исключаются 2(m + n) неизвестных и их остается ровно
(m – 1)(n – 1).

Было показано, что при h → 0 и k → 0 решение разностного уравнения приближается к решению дифференциального уравнения в случае уравнений эллиптического типа.

В случае параболических и гиперболических уравнений необходимо соблюдение некоторых ограничений.