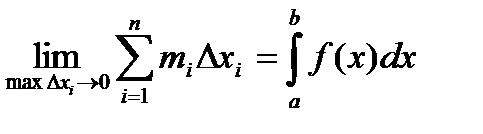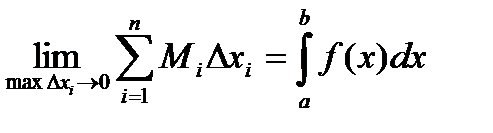Интегрирование тригонометрических функций
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 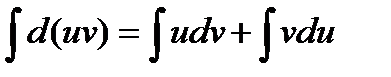 , а в соответствии с свойствами неопределенного интеграла:
, а в соответствии с свойствами неопределенного интеграла:
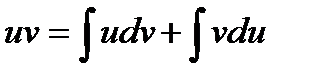 или !
или ! 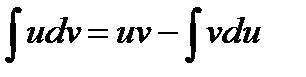 ; {при условии, VdU проще чем UdV}
; {при условии, VdU проще чем UdV}
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
4. Разложение прав. рац. дроби в сумму простейших. Интегрирование рац. дробей.
Определение: Рац. дробью называется ф-ция:
f(x) = P(x)/Q(x), где P(x), Q(x) – взаимно пропорциональные мн-ва.
P(x) = b0+b1x+…+bmxm
Q(x) = a0+a1x+…+anxn
Если m<n f(x) – правильная дробь
m>=n – неправильная дробь
Теорема: Пусть знаменатель Q(x) прав. рац. дробь P(x)/Q(x) имеет действ. корень х=а кратности К, сущ. const A ≠ 0, такая, что справедливо равенство:
P(x)/Q(x) = P(x)/((х-а)кQ1(x)) = (А/(х-а)к) + (P1(x)/((х-а)к-1Q1(x))), при Q1(а) ≠ 0
Док-во: Составим разность: (P(x)/((х-а)кQ1(x)) – (А/(х-а)к ) = (P(x) – А*Q1(х)) / ((х-а)кQ1(x)) = | A выбираем так, чтобы х=а было корень числ.| = P(a) – Aa1(a) = 0
A = P(a)/ Q1(x),
(P(x) – А*Q1(х)) / ((х-а)кQ1(x)) = (a-x)*P1(x) / (a-x)*Q1(x)
Теорема: Пусть знаменатель Q(x) паравільная рац. дробь, P(x)/Q(x) имеет пару комплекс. корней кратности K, кот. соответствуют (х2+px+q) разложению Q(x), тогда сущ. const A и В, что справедливо разложение P(x)/Q(x) = P(x) / (х2+px+q)2*Q1(x) = (Ах+В) / (х2+px+q)2 +
P1(x) / (х2+px+q)2*Q1(x).
теоремы разложения следует: всякую прав. рац. дробь можно разложить в сумму простейших рац. дробей типа I – IV и это разложение единственное.
4-5.Интегрирование простейших рациональных дробей.
Определение: Рац. дробью называется ф-ция:
f(x) = P(x)/Q(x), где P(x), Q(x) – взаимно пропорциональные мн-ва
Определение: Элементарныминазываются дроби следующих четырех типов:
I. 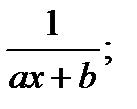 III.
III. 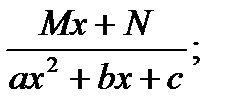
II. 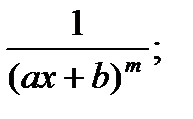 IV.
IV. 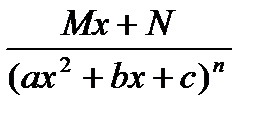
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 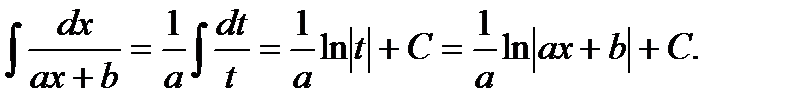
II. 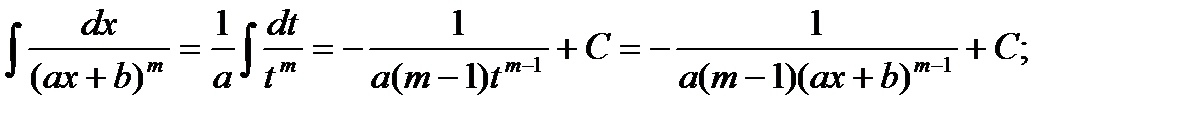
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
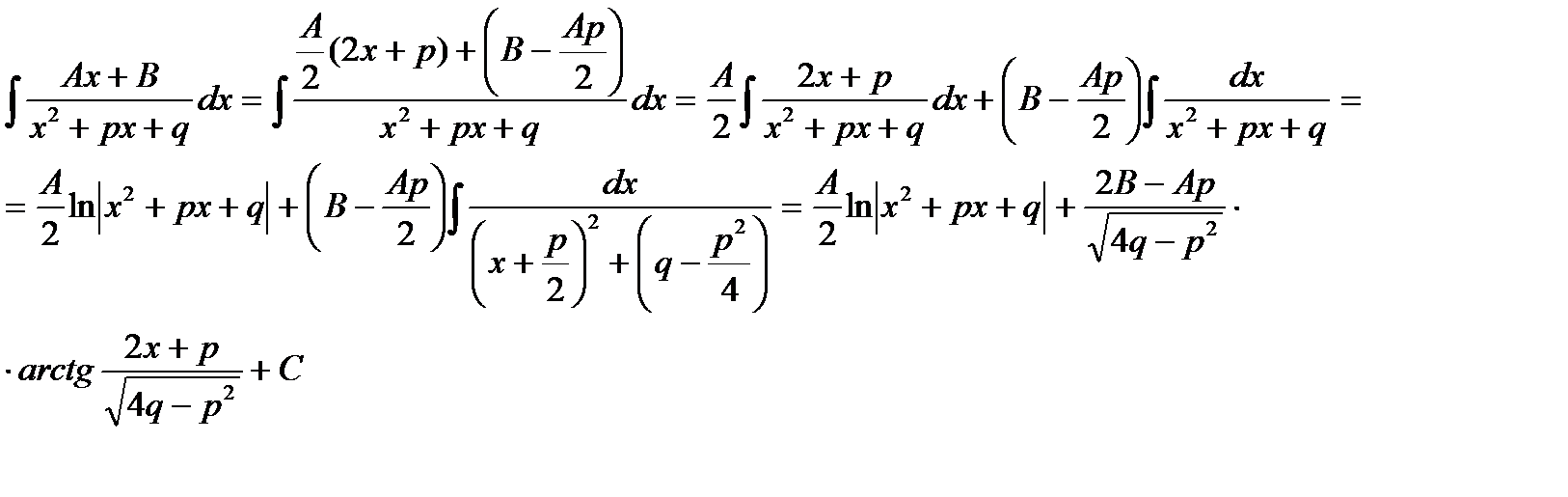
IV. ∫(Ax+B)/(x2+px+q)k*dx = |x+p/2 = t; dx=dt; q-p2/4 = ±m2| =A*∫(d(t2+a2))/2(t2+a2)k + (B-Ap/2)*∫(dt/(t2+a2)k = (A/2)*(1/(1-k))*(1/( t2+a2)k+1) + (B-Ap/2)Jk
6
Интегрирование тригонометрических функций.
1) Интеграл вида 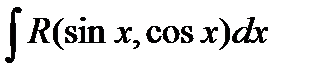 .
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с помощью подстановки 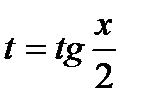 . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
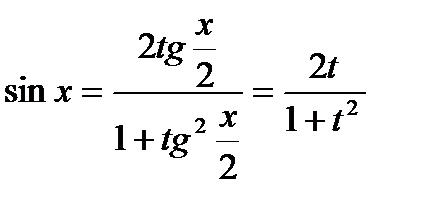 ,
, 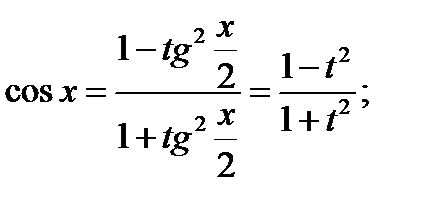
Тогда 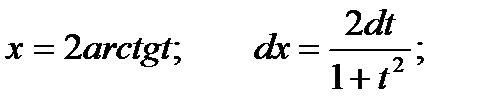
Таким образом: 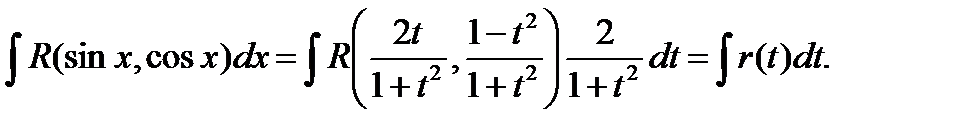
Описанное выше преобразование называется универсальной тригонометрической подстановкой.
2) ∫ соsmx*sinnxdx, где m,n – нат. числа
а) пусть m = 2p+1
∫соs2p+1x*sinnxdx = ∫ (1-cos2x)p*sinnxdx*d(sinx) = ∫ (1-U2)p*UndU, если n=2p+1, то синус выносится под знак диф-ла
sin dx = -d(cosx)
б) m = 2p, n=2q
∫соs2px*sin2qdx = ∫((1+cos2x)/2)p*((1-cos2x)/2)q*d(sinx)
3) Интеграл произведения синусов и косинусов различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
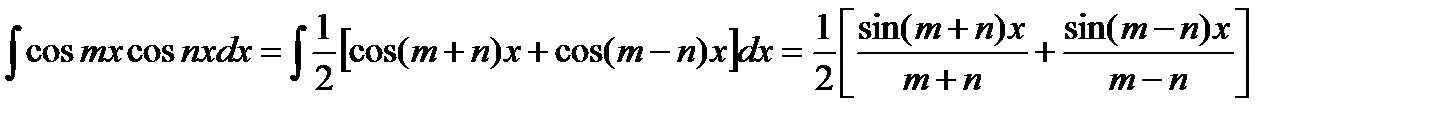
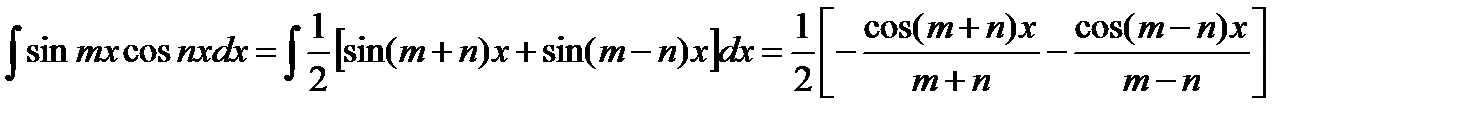
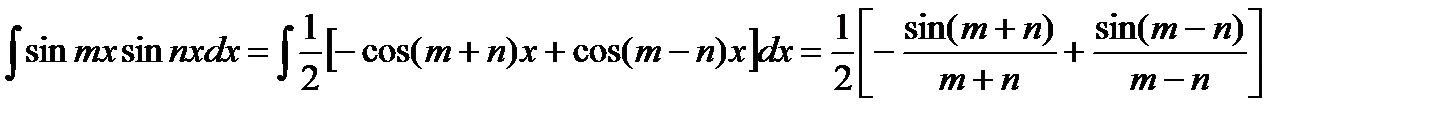
7. Интегрирование иррац-тей.
1. ∫R(x, n√x)dx, R – рац. выражение – над х и n√x проведено конечное число арифмет. операций.
= |x=tk, dx=ktk-∙1dt, k – НОК| = ∫R(tk, t)ktk-1dt
2. Интеграл вида 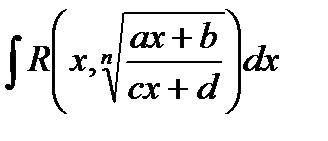 где n- натуральное число.
где n- натуральное число.
С помощью подстановки 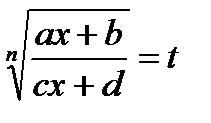 функция рационализируется.
функция рационализируется.
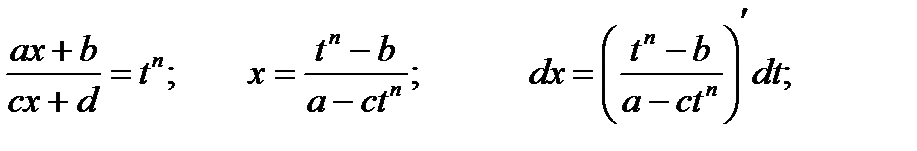
Тогда 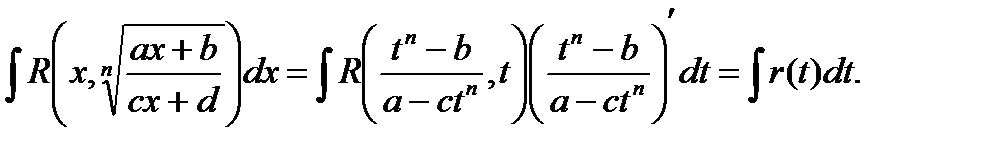
8. Задачи, приводящие к понятию определения ОИ
Определение Ньютона:Пусть ф-ция f(x) имеет смысл на [а, b] первообразную F(x), тогда определенным інтегралом ф-ции f(x) на [а, b] называется число F(b) - F(а)
а∫bf(x)dx = F(b) - F(а) = F(x)|ab
Задачи: (для Римана)
1)площадь криволинейной трапеции
2)масса отрезка с переменной плотностью
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма 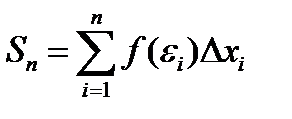 стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
Обозначение : 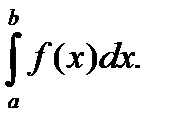
а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции f(x) существует предел 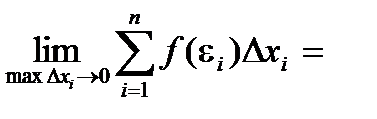
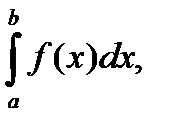 то функция называется интегрируемой на отрезке [a, b].
то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения: 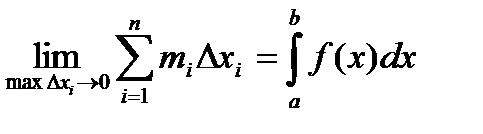
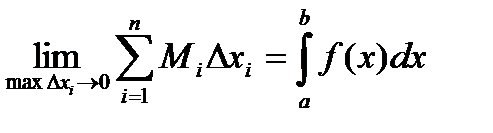
9. Определение ои как предела инт суммы. Св ои.
1) 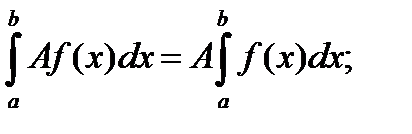
2) ∫abkdx = k(b-a)- вытекает из определения, т.к. ∑k=0n-1f(сиj)дельтахj =
∑k=0n-1 kдельтахj =k ∑k=0n-1 дельтахj = k(b-a)
3) 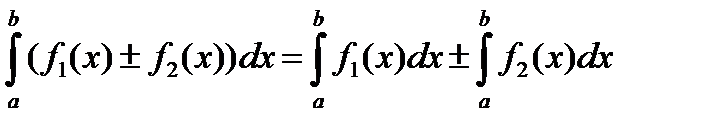 - св-во линейности
- св-во линейности
4) Пусть ф-ция f(x) кусочно-постоянная на отрезке [a,b], т.е. сущ. разбиение отрезка [a,b] на (xk, xk+1) ф-ция f(x) принимает постоян зн-ние lk:
∫abf(x)dx = ∑ab lk дельта xk
5) 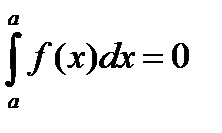
6) 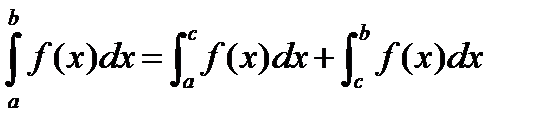 - свойство аддитивности
- свойство аддитивности
7) Если f(x) £ j(x) на отрезке [a, b] a < b, то 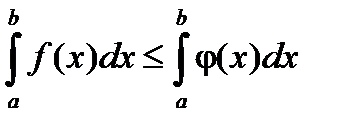
8) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то: 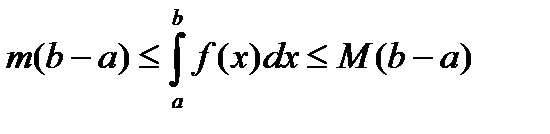
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма 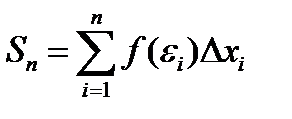 стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
О. Если для функции f(x) существует предел 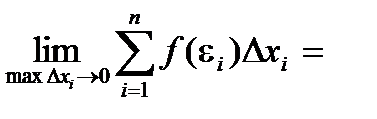
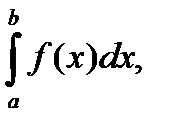 то функция называется интегрируемой на отрезке [a, b].
то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения: