Теорема Чебышева (закон больших чисел)

Пусть X случайная величина с математическим ожиданием M(X) и дисперсией D(X). Будем проводить серии из n независимых опытов и вычислить среднюю арифметическую 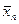от значений X этих серий. Тогда для любого e > 0 вероятность того, что 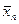отличается от M(X) на величину больше, чем e, стремится к нулю

P(| 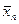– M(X)| > e) ® 0 при n ® ¥.

Теорема показывает, что при очень большом числе случайных величин средний их результат перестает быть случайной величиной и стремится к постоянной величине M(X).

Теорема Бернулли

Пусть событие A имеет вероятность p.Будем проводить серии из n независимых опытов и вычислить частоту m/n поступления события A в таких сериях. Тогда для любого e > 0 вероятность того, что частота m/n отличается от p на величину больше, чем e, стремится к нулю

P(|m/n – p| > e) ® 0 при n ® ¥.

Теорема Бернулли устанавливает связь между вероятностью появления события и его относительной частотой появления и позволяет при этом предсказать, какой примерно будет это частота в n испытаниях. Из теоремы видно, что отношение m/n обладает свойством устойчивости при неограниченном росте числа испытаний.

В частности, опыты показывают , что при подбрасывании монеты частота появления герба приближается к ½ при n порядка нескольких тысяч.

Центральная предельная теорема

Если случайные величины X₁, X₂, … X_n независимы и имеют конечные математические ожидания и дисперсии, то при n ® ¥, вероятность того, что отклонение средней арифметической от значений X этих серий не превзойдет M(X) по абсолютной величине некоторую величину, равна функции Лапласа:

,

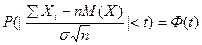где M(X) и σ математическое ожидание и среднее квадратичное отклонение случайных величин X_i.

Если сложить большое число случайных величин, имеющих один или различные законы распределения, то случайная величина, являющаяся результатом суммы, при некоторых условиях, будет иметь нормальный закон распределения. На опыте было установлено, что уже при числе слагаемых, большем 10, распределение суммы можно заменить нормальным.

Вариационные ряды: числовые характеристики вариационных рядов

Вариационные ряды

В реальных социально-экономических системах нельзя проводить эксперименты, поэтому данные обычно представляют пассивные наблюдения за производящим процессом, например: курс валюты в бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений, в общем случае, ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить.

Операция расположения значений статистических данных по росту, называется ранжированием. Ранжирование позволяет сгруппировать одинаковые баллы (элементы ряда). Отличающиеся друг от друга элементы x называют вариантом. Число элементов в каждой группе обозначим через m. Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация от английского слова «variation» - изменение).

Если количественный признак принимает дискретное число значений, то соответствующий вариационный ряд называется дискретным.

@ Задача 1: На основании данных тестирования 20 учащихся: 3, 2, 4, 5, 3, 4, 2, 3, 4, 5, 2, 3, 3, 4, 3, 5, 2, 5, 5, 3 построить вариационный ряд.

Решение: Ранжированный ряд представляет: 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5. Итак, число вариантов всего 4 (x = 2; 3; 4; 5) и, следовательно, статистический ряд состоящий из 20 членов переписывается как:

x	2	3	4	5
m	4	7	4	5

Отношение m к числу n - объему совокупности (в приведенной задаче число тестированных учащихся) называется частотой p = m/n , Σm = n, Sp = 1.

В приведенном примере p = 0,2; 0,35; 0,2; 0,25.

Если количественный признак изменяется непрерывно, или принимает много значений, то диапазон изменения признака разбивается на интервалы. Это случай интервального вариационного ряда. Для построения такого ряда промежуток изменения элемента разбивается на ряд отдельных интервалов и подсчитывается количество значений величины в каждом из них.

Число интервалов k определяется по формуле Стерджесса k = 1 + 3,322lgn, а длина h интервала определяется как

,

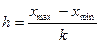где x_max, x_mun - наибольший и наименьший варианты статистического ряда, а их разность называется размахом статистического ряда.

@ Задача 2. Стаж работы 22 учителей характеризуется следующими данными: 0, 5, 20, 25, 6, 16, 7, 3, 8, 15, 12, 6, 13, 14, 23, 10, 18, 11, 13, 7, 9, 8. Данные представить в виде интервального вариационного ряда.

Решение: По формуле Стерджесса получим k = 1 + 3,322lg22 » 5, а потом и h = 25/5 = 5. Таким образом, статистические данные можно переписать в виде следующего интервального вариационного ряда:

x	[0; 5]	(5; 10]	(10; 15]	(15; 20]	(20; 25]
m

Замечание: Если количество значений в одном интервале менее 3-5 при достаточно больших n, то обычно объединяют соседние интервалы, переходя к рядам с неравными интервалами. В приведенном примере можно соединить последние два интервала.