Неравенство Чебышева. Закон больших чисел.

Теорема (неравенство Чебышева). Если случайная величина Х имеет конечные математическое ожидание Ь(Х) и дисперсию D(X), то при любом сколь угодно малом ε>0 справедливо неравенство.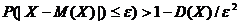

Теорема Чебышева. При достаточно большом числе n независимых испытаний среднее арифметическое наблюдаемых значений случайной величины Х сходится по вероятности к ее математическому ожиданию М(Х), то есть 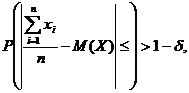где ε – достаточно малое положительное число, δ – зависит от ε и удовлетворяет неравенству: , где D(X) – дисперсия Х.

интегральная теорема Муавра-Лапласа

Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1 ,то вероятность 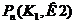того,что событие А появится в n испытаниях от К1 до К2 раз,приближенно = определенному интегралу:

,

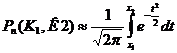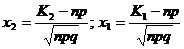
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.

Основные задачи математической статистики. Генеральная и выборочные совокупности. Выборка. Вариационный и статистический ряды. Гистограмма частот. Эмпирическая функция распределения. Точечные и интервальные оценки. Несмещенная, эффективная, состоятельная оценка.

Математическая статистика разрабатывает методы планирования и анализа эксперимента.

К типичным задачам математической статистики относятся:

- задача определения закона распределения случайной величины по статистическим данным;

- задача нахождения неизвестных параметров распределения случайной величины;

- задача проверки правдоподобия выдвигаемых по статистическим данным гипотез о законе распределения случайной величины, о ее параметрах.

Выборочной совокупностью (или выборкой) называется совокупность случайно отобранных объектов.

Генеральной совокупностью называется совокупность всех однородных объектов, из которых производиться выборка.

Объемом совокупности (генеральной или выборочной) называется число объектов этой совокупности.

Выборка называется представительной (или репрезентативной), если она осуществлена случайным образом, когда все объекты генеральной совокупности имели равные вероятности попасть в выборку.

Вариационным рядомвыборки (1.1) называется способ ее запи­си, при котором элементы Xi упорядочиваются по величине, то есть записываются в виде последовательности в порядке их возрастания (верхний индекс), а не в порядке измерений (нижний индекс).

х⁽¹⁾, х⁽²⁾, ... ,х⁽ⁿ⁾, причем х⁽¹⁾ <= х⁽²⁾ < ... < х⁽ⁿ⁾. Каждое значение хi; вариационного ряда называется вариантой.

Разность между максимальным и минимальным элементами вы­борки х⁽ⁿ⁾- х ⁽¹⁾=w называется размахом выборки.

Пусть в выборке объемом n элемент хi встречается niраз. Число ni называется частотой элемента xi . Очевидно, что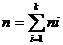

Статистическим рядомназывается последовательность пар (xi,ni), которая записывается в виде табл. 1.Таблица 1(Статистическим рядом, соответствующим полученной случайной выборке, называется набор значений (вариант) качественного или количественного признака объектов выборки, которые располагаются в порядке возрастания. )

Xi	X1	х2	..	хк
ni	n1	n2	..	Nк

Отношение wi= ni/n называется относительной частотой, или ча­стностью элемента хi, выборки. Статистическим распределением случайной величины X называется последовательность пар (хi ,wi), которая также записывается в виде табл. 2.

Таблица 2

Xi	X1	Х2		Xk
wi	w1	w2	…	wk

k

Заметим, что E(сумма)i=lwi=1.

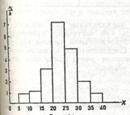
Гистограммой ча­стот называют ступен­чатую фигуру, состоя­щую из прямоугольни­ков, основаниями кото­рых служат частичные интервалы длиною h, а высоты равны отноше­нию пi/h (плотность ча­стоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии пi/h. Площадь i-го частичного прямоугольника равна hпi/h=пi—сумме частот вариант i-го интервала; следо­вательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.

На рис. изображена гистограмма частот распреде­ления объема n = 100

Эмпирической функцией распределения случайной величины X называется функция F* (х), определяющая для каждого значения х относительную частоту события (Х< х), т. е. функция вида F* (x)=m/n, ( 1.3 )

где m - число выборочных значений меньших х(хi<х),ап - объем выборки.

Свойства F*(x) аналогичны свойствам теоретической функции распределения F(x) и вытекают непосредственно из определения (1.3), т. е.:

1) значения эмпирической функции распределения заключены
между 0 и 1

О < F*(x) <1 ;

2) F *(х) есть неубывающая функция аргумента х ;

3) F *(х)=0 при х< =хi (х i - наименьшая варианта) ; F *(х)=1 при х> х _k (x _k - наибольшая варианта).

Точечные статистические оценки параметров распределения.

Пусть собранный и обработанный статистический материал представлен в виде статистического ряда. Точечной оценкой наз оценку кот определяется одним числом. при выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, те приводить к грубым ошибкам.

Точечной статистической оценкой параметра а распределения случайной величины называется приближенной значений а* этого параметра, вычисленное по статистическим данным.

Любая точечная статистическая оценка некоторого параметра, вычисляемая на основе статистического ряда, должна удовлетворять трем требованиям:

1) при увеличении числа испытаний она должна находиться по вероятности к оцениваемому параметру (свойство состоятельности);

2) математическое ожидание статистической оценки (как случайной величины при изменении числа испытаний) равно оцениваемому параметру (свойство несмещенности);

3) при заданном объеме выборки статистическая оценка имеет наименьшую дисперсию (свойство эффективности)

Интервальной наз оценку, кот определяется двумя числами Qj * и Q₂* – концами интервала, при этом Q попадает в интервал Q1*< Q < Q₂*. Интервальные оценки позволяют установить точность и надежность оценок.

Качество оценок характеризуется некоторыми свойствами. Сфор­мулируем основные из них.

Свойство 1.

Оценка Q* называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть, если M(Q*)=Q.Замечание: Несмещенная оценка является точной в среднем, то есть не­смещенность оценки гарантирует отсутствие систематической ошибки.

Свойство 2.

Оценка Q*(n)=U(xi,x₂,...,x_n) величины Q называется состоя­тельной, если при п —> 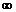она сходится по вероятности к Q, то есть при любом е>0 limP(|Q*(n)-Q|<_E)=l.

n—»

Замечание:Состоятельность оценки гарантирует при п ->оо сколь угод­но большую точность оценки с вероятностью, сколь угодно близкой к единице.

Свойство 3.

Несмещенная оценка Q*=U(xi,x₂,...,x_n) величины Q называет­ся эффективной,если ее дисперсия минимальна по сравнению с дис­персиями других несмещенных оценок величины Q при любом, но од­ном и том же п, то есть D(Q*)=M[(Q*-Q)²]=min.

Замечание:Эффективность оценки гарантирует минимум средней квадратической ошибки M[(Q*-Q)²].