Задачи для самостоятельного решения.
2.1.Найти матрицы: 1) 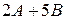 ; 2)
; 2) 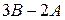 ; 3)
; 3) 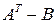 ; 4)
; 4) 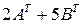 , если
, если
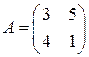 ,
, 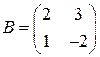 .
.
2.2.Найти матрицы: 1) 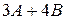 ; 2)
; 2) 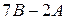 ; 3)
; 3) 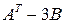 ; 4)
; 4) 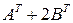 , если
, если
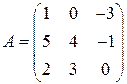 ,
, 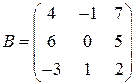 .
.
2.3.Найти произведения 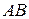 и
и 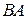 матриц
матриц  и
и 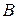 , если
, если
1) 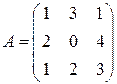 ,
, 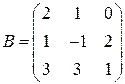 ;
;
2) 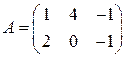 ,
, 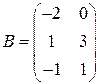 ;
;
3) 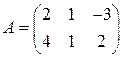 ,
, 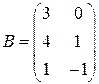 ;
;
4) 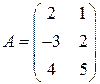 ,
, 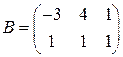 .
.
2.4.Даны матрицы
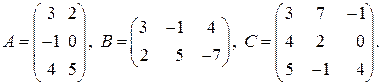
Какие из произведений 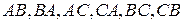 определены? Найти их.
определены? Найти их.
2.5.Даны матрицы
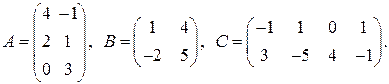
Определены ли произведения 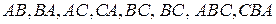 ?Если да, то найти их.
?Если да, то найти их.
2.6.Дана матрица  . Найти
. Найти 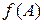 , если
, если 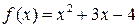 и
и
1) 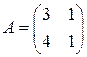 ; 2)
; 2) 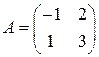 ; 3)
; 3) 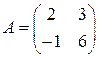 .
.
2.7.Дана матрица А. Найти 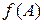 , если
, если 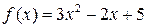 .
.
1) 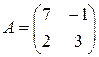 ; 2)
; 2) 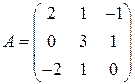 ; 3)
; 3) 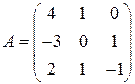 .
.
2.8.Найти матрицы:
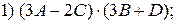
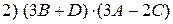 ;
;
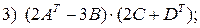
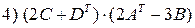 , если
, если
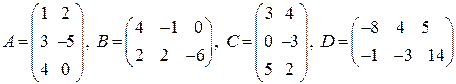 .
.
2.9.Вычислить определители:
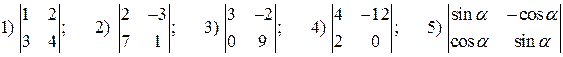 .
.
2.10.Вычислить определители:
1) 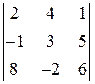 ; 2)
; 2) 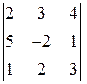 ; 3)
; 3) 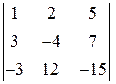 ;
;
4) 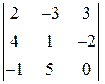 ; 5)
; 5) 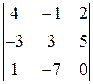 ; 6)
; 6) 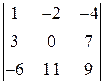 ;
;
7) 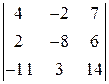 ; 8)
; 8) 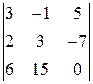 .
.
2.11.Вычислить определители:
1) 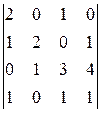 ; 2)
; 2) 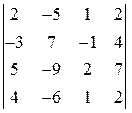 ; 3)
; 3) 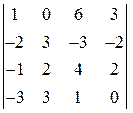 ;
;
4) 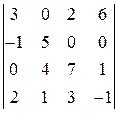 ; 5)
; 5) 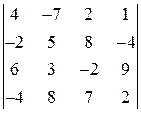 ; 6)
; 6) 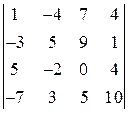 .
.
2.12.Дана матрица  . Найти обратную матрицу. Выполнить проверку, если
. Найти обратную матрицу. Выполнить проверку, если
1) 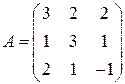 ; 2)
; 2) 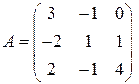 ; 3)
; 3) 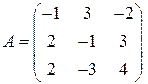 ;
;
4) 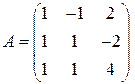 ; 5)
; 5) 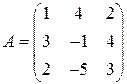 ; 6)
; 6) 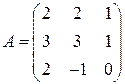 ;
;
7) 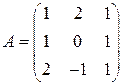 ; 8)
; 8) 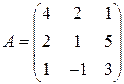 .
.
2.13.Найти обратную матрицу для матрицы  . Сделать проверку.
. Сделать проверку.
1) 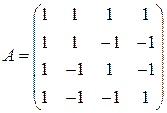 ; 2)
; 2) 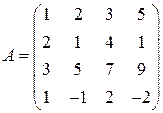 ; 3)
; 3) 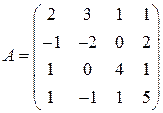 .
.
2.14.Решить матричные уравнения:
1) 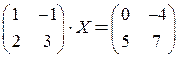 ; 2)
; 2) 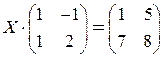 ;
;
3) 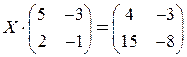 ; 4)
; 4) 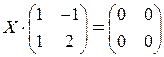 ;
;
5) 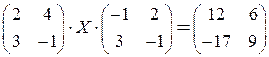 ; 6)
; 6) 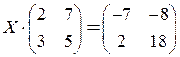 ;
;
7) 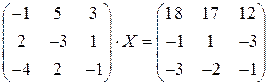 ; 8)
; 8) 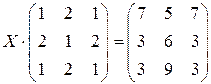 ;
;
9) 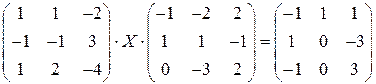 .
.
2.15.Вычислить:
1) 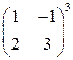 ; 2)
; 2) 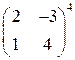 ; 3)
; 3) 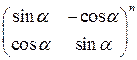 ; 4)
; 4) 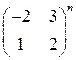 .
.
2.16.Матрицы  и
и 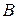 называются перестановочными, если
называются перестановочными, если 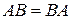 . Найти все матрицы перестановочные с матрицей
. Найти все матрицы перестановочные с матрицей  , если
, если
1) 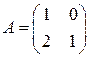 ; 2)
; 2) 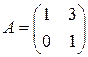 ;
;
3) 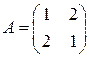 ; 4)
; 4) 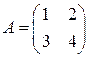 .
.
2.17.Найти ранг матриц методом окаймления миноров:
1) 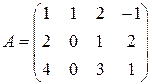 ; 2)
; 2) 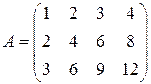 ;
;
3) 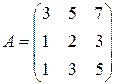 ; 4)
; 4) 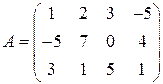 ;
;
5) 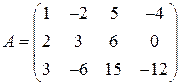 ; 6)
; 6) 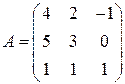 .
.
2.18.При помощи элементарных преобразований найти ранг матриц:
1) 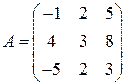 ; 2)
; 2) 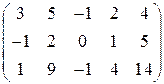 ; 3)
; 3) 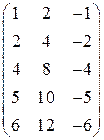 ;
;
4) 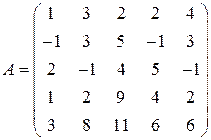 ; 5)
; 5) 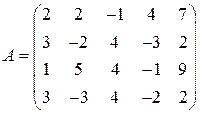 .
.
Тема 2.2 системы линейных уравнений
Системой  линейных уравнений с
линейных уравнений с 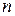 неизвестными называется система вида
неизвестными называется система вида
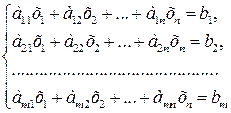 (2.11)
(2.11)
Система уравнений (2.11) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если решений больше одного.
Множество всех решений системы (2.11) называется ее общим решением. Решить систему – значит найти ее общее решение.
Две системы уравнений называются эквивалентными, если они имеют одинаковые множества решений или обе несовместны.
Элементарными преобразованиями системы линейных уравнений называются такие преобразования:
перестановка уравнений;
умножение обеих частей уравнения на одно и тоже число, не равное нулю;
прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на одно и тоже произвольное число;
удаление (вычеркивание) из системы тривиального уравнения вида 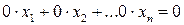 .
.
В результате элементарных преобразований получаем систему, эквивалентную исходной.
Линейное уравнение называется однородным, если его свободный член равен нулю. Система, состоящая из однородных уравнений, называется однородной.
Рассмотрим матрицы
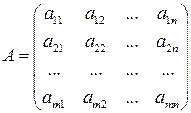 ,
, 
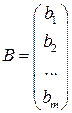 , (2.12)
, (2.12)
где  – матрица коэффициентов системы (или матрица системы)
– матрица коэффициентов системы (или матрица системы)
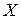 – матрица (вектор – столбец) неизвестных переменных;
– матрица (вектор – столбец) неизвестных переменных;
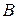 – матрица (вектор – столбец) свободных членов.
– матрица (вектор – столбец) свободных членов.
Тогда систему (2.11) можно записать так:
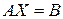 . (2.13)
. (2.13)
Уравнение (2.13) называется матричной формой записи системы линейных уравнений (2.11).
Матрица вида
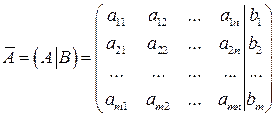 (2.14)
(2.14)
называется расширенной матрицей системы.
Исследование совместимости систем
