Уравнение прямой в пространстве

Прямая может быть задана как пересечение двух плоскостей. В этом случае она задается системой уравнений, определяющих эти плоскости:

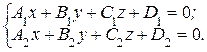(6)

Каноническое уравнение прямой:

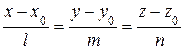. (7)

Здесь М(x₀, y₀, z₀) – точка, через которую проходит прямая, (l, m, n) – направляющий вектор прямой.

Это уравнение на самом деле представляет собой систему двух уравнений, как и в формуле (6). Один или два знаменателя могут быть равны 0, это будет означать, что соответствующие числители приравниваются к 0.

Уравнение прямой, проходящей через две данные точки М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂):

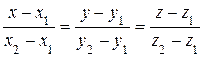. (8)

Пример 1.7.1.В пространстве заданы точки A(3, 2, –1), В(2, –1, 2) С(1, 3, 4), D (4, –5, 5). а) постройте уравнение плоскости (АВС); б) Найдите расстояние от точки D до плоскости (АВС); в) постройте уравнение прямой АС; г) постройте уравнение перпендикуляра к плоскости (АВС), проходящего через точку D.

Решение. а) Воспользуемся формулой (4):

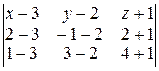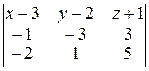= 0;

= 0;

(x – 3)( –15 – 3) – (y – 2)( –5 + 6) + (z + 1)( –1 – 6) = 0;

–18(x – 3) – (y – 2) – 7(z + 1) = 0;

–18x + 54 – y + 2 – 7z – 7 = 0;

–18x – y – 7z + 49 = 0;

18x + y + 7z – 49 = 0.

б) Воспользуемся формулой (5):

.

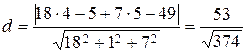в) Воспользуемся формулой (8):

;

.

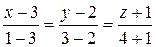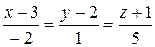г) Направляющим вектором перпендикуляра является нормаль к плоскости; из пункта а) это 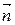= (18, 1, 7). Воспользуемся формулой (7):

.

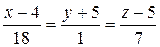У п р а ж н е н и я

1.7.1.В пространстве даны точки А(1; 3; 0), B(–1; 2; 1), C(–2; 1; 3), D (2; 2; 1).

а) Постройте уравнение плоскости АВС;

б) Постройте уравнение прямой ВС;

в)Постройте уравнение перпендикуляра, проведенного к плоскости АВС через точку D;

г) Найдите расстояние от точки D до плоскости АВС;

д) Постройте уравнение плоскости, проходящей через точку D параллельно плоскости АВС.

Преобразование координат

Часто для определения вида и параметров фигуры, задаваемой уравнением в некоторой системе координат, бывает удобно перейти к другой системе координат. Это может упростить уравнение.

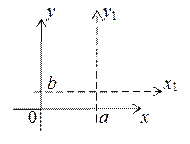
Простейшее преобразование – это параллельный перенос координатных осей. Пусть новые координатные оси x₁ и y₁ имеют в старых координатах уравнения x = a, y = b. Тогда новые координатные оси выражаются через старые формулами x₁ = x – a, y₁ = y – b, а старые через новые формулами x = x₁+ a, y = y₁+ b. Например, уравнение окружности с центром в точке А(a, b) и радиусом r в старых координатах имеет вид (x – a)² + (y – b)² = r², а в новых x₁² + y₁² = r².

Другой вид преобразований системы координат – это поворот координатных осей вокруг начала координат на угол a (угол отсчитывается против часовой стрелки). Формулы перехода от старой системы к новой задаются уравнениями

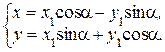
Формулы перехода от новой системы к старой задаются уравнениями

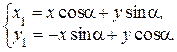
Можно использовать и косоугольную систему координат, в которой оси расположены под произвольным углом и длины единичных отрезков по осям абсцисс и ординат различны. В такой системе прямые линии и многие другие фигуры задаются уравнениями тех же типов, что и в прямоугольной, но параметры уравнений изменяются; становится весьма проблематично определять расстояния и углы. Но использование косоугольной системы координат позволяет упрощать преобразование уравнений в тех случаях, когда требуется определить только тип фигур, задаваемых этими уравнениями. Преобразование координат производится по формулам

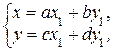
где ad – bc ¹ 0.

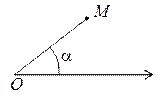Совершенно другой вид системы координат, отличный от декартовой, – это полярная система координат. Она задается точкой (полюсом) О и полярной осью – лучом, выходящим из полюса. Положение любой точки М на плоскости задается углом a, который луч ОМ образует с полярным лучом, и радиус-вектором r – длиной отрезка ОМ. Эти два параметра полностью определяют положение точки М. При этом радиус-вектор определяется однозначно, а угол с точностью до периода 2p: этот период соответствует полному обороту вокруг полюса, приводящему к тому же направлению. Например, уравнение окружности с центром в полюсе и радиусом R в полярной системе имеет вид r = R.

От декартовой к полярной системе координат можно перейти по формулам x = r cos a, y = r sin a. Обратный переход производится с помощью формул

r = ;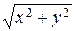

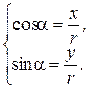
Кривые второго порядка

Уравнение второго порядка – это уравнение вида

Ax² + Bxy + Cy² + Dx + Ey + F = 0.

Такое уравнение преобразованиями координат приводится к одному из следующих видов:

Уравнение	Фигура
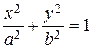	Эллипс
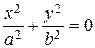	Точка
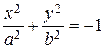	Пустое множество (мнимый эллипс)
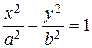	Гипербола
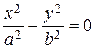	Пара пересекающихся прямых
y2 = 2px, p>0	Парабола
y2 = а2, а ¹ 0	Пара параллельных прямых
y2 = –а2, а ¹ 0	Пустое множество (пара мнимых параллельных прямых)
y2 = 0	Прямая (пара совпавших прямых)

Эллипс

Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.

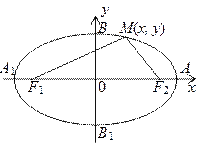Выведем уравнение эллипса. Для этого расположим координатные оси так, чтобы фокусы F₁ и F₂ располагались на оси абсцисс симметрично относительно начала координат. Пусть расстояние между ними равно 2с, значит, они имеют координаты
F₁(–с, 0) и F₂(с, 0). Пусть M(x, y) – произвольная точка эллипса. Тогда из определения эллипса получаем уравнение

MF₁ + MF₂ = 2a.

Подставляем MF₁ = 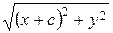, MF₂ = 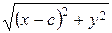, получаем

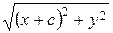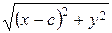+ = 2а.

Это уравнение приводится к виду

(a² – c²)x² + a²y² = a²(a² – c²).

При этом a >c, поэтому a² – c² > 0, и можно ввести обозначение a² – c² = b². Уравнение тогда приводится к виду b²x² + a²y² = a²b². Разделив его на a²b², получим каноническое уравнение эллипса

.

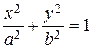Эллипс симметричен относительно координатных осей и пересекает ось абсцисс в точках А₁(–с, 0) и А(с, 0), ось ординат в точках B₁(–b, 0) и B(b, 0). Эти четыре точки называются вершинами эллипса. Отрезок А₁А называется большой осью эллипса, отрезок В₁В – малой осью. Таким образом, а и b – это длины большой и малой полуосей.

Эксцентриситетом эллипса называется число 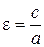. Для любого эллипса 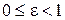. Эксцентриситет характеризует степень сжатия эллипса: чем ближе эксцентриситет к 1, тем сильнее сжат эллипс. При 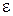= 0 эллипс является окружностью. При этом фокусы эллипса сливаются в одну точку, совпадающую с центром эллипса.

Гипербола

Гиперболой называется множество точек плоскости, для каждой из которых разность расстояний до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.

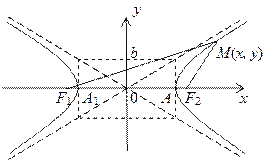Уравнение гиперболы выводится аналогично уравнению эллипса из равенства

ïMF₁ – MF₂ï = 2a.

Здесь фокусы имеют координаты F₁(–с, 0) и F₂(с, 0), c > b и c² – a²= b². После преобразований получаем уравнение

.

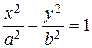Гипербола симметрична относительно обеих координатных осей. Она состоит из двух ветвей. Гипербола пересекает ось абсцисс в двух точках А₁(–а, 0) и А(а, 0), которые называются вершинами гиперболы.

Прямые 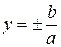называются асимптотами гиперболы. Они могут строиться с помощью четырех прямых, параллельных осям: х = 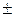а, у = 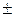b. В пересечении этих прямых образуется прямоугольник, который называется основным прямоугольником гиперболы.

Эксцентриситетом гиперболы называется число 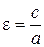. Для любой гиперболы 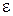> 1. Эксцентриситет характеризует степень сжатия гиперболы: чем ближе эксцентриситет к 1, тем сильнее вытянут основной прямоугольник гиперболы.

Парабола

Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой (предполагается, что фокус не лежит на директрисе).

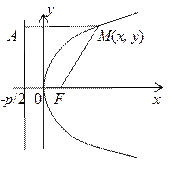Для вывода уравнения параболы проведем ось абсцисс через фокус перпендикулярно директрисе, ось ординат поместим между фокусом и директрисой на одинаковом расстоянии от них. Расстояние от фокуса до директрисы обозначим через р, это число называется параметром параболы. Фокус будет иметь координаты F(p/2, 0) уравнение директрисы x = –p/2.

Уравнение параболы выводится из равенства

MF = MА.

После преобразований получаем уравнение

y² = 2px.

Парабола имеет ось симметрии, которая называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. В отличие от гиперболы парабола не имеет асимптот.

Все параболы подобны друг другу. Значит, если сжать или растянуть параболу в любом направлении, получим подобную параболу.