Наибольшее и наименьшее значение функции

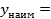__ и достигается в любой точке вида x=__________

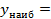__ и достигается в любой точке вида x=__________

Непрерывность функции.

Функция __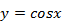

Область значений.

______________

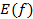II. Построение графика функции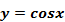

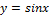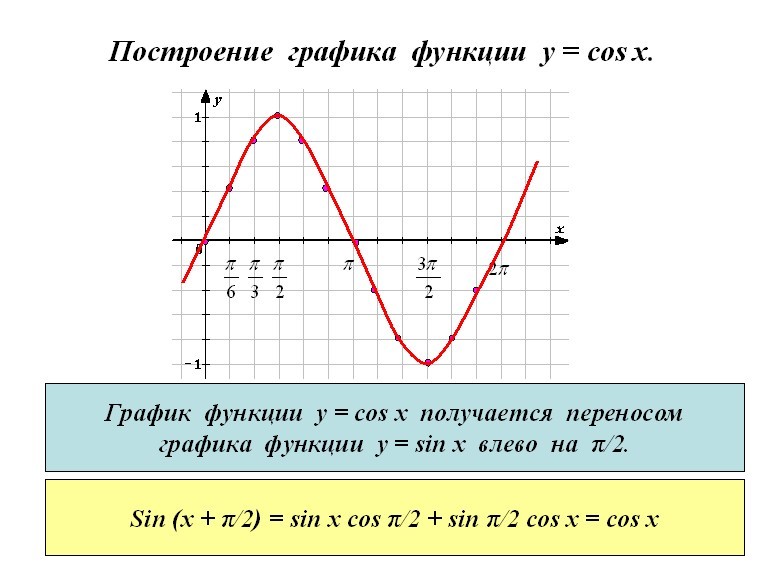
График функции 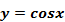- косинусоида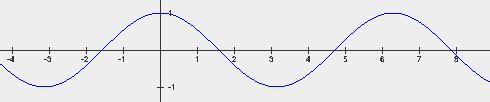

Упражнения:

1. Рассмотреть по учебнику графическое решение уравнения .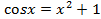

По аналогии решить уравнение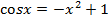

2. Построить и прочитать график кусочной функции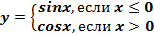

1. Область определения _________________________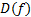

2. Чётность, нечётность: _____________________________

3. Монотонность функции: ___________________________
4. Ограниченность функции: __________________________

5. Наибольшее и наименьшее значение функции.

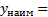__ и достигается в любой точке вида x=_______

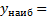__ и достигается в любой точке вида x=_______

6. Непрерывность функции:___________________________

7. Область значений _____________________________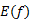

Периодичность функций

Определение. Функцию 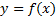, 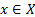называют периодической, если существует такое отличное от нуля число Т, что для любого х из множества X выполняется двойное равенство 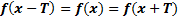,гдеT - период функции .

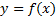Отсюда следует, что, поскольку для любого х справедливы равенства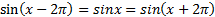

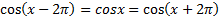
Периодичность — это восьмое свойство функций синус и косинус

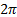то, функции синус и косинус являются периодическими, причем число служит периодом этих функций.

Если функция имеет период Т, то для построения графика функции нужно сначала построить ветвь (волну, часть) графика на любом промежутке длины Т, а затем сдвинуть эту ветвь по оси х вправо и влево на Т, 2Т, ЗТ и т. д.

Упражнения:

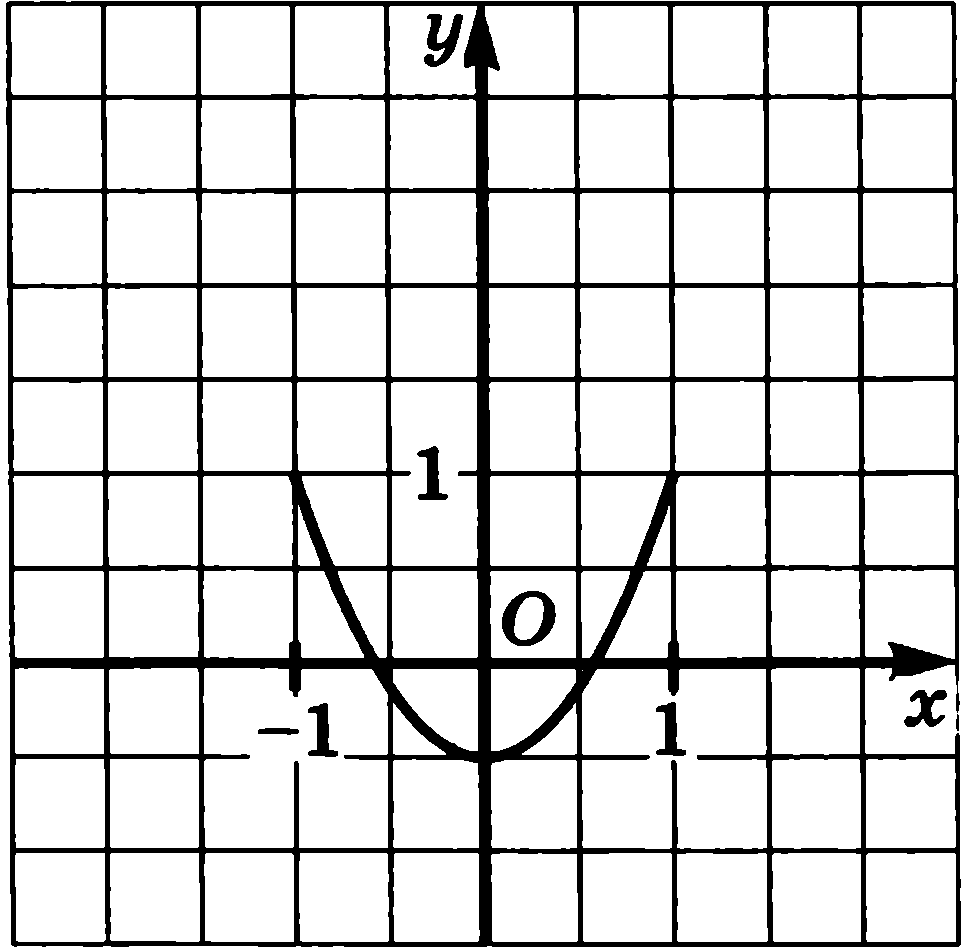
1. На рисунке изображена часть графика периодической функции на отрезке [-1; 1], длина которого равна периоду функции. Постройте график функции:

а) на отрезке [1; 3];

б) на отрезке [-3; -1];

в) на отрезке [3; 7];

г) на всей числовой прямой.

Решение:

а) на отрезке [1; 3];

б) на отрезке [-3; -1];

в) на отрезке [3; 7];

г) на всей числовой прямой.

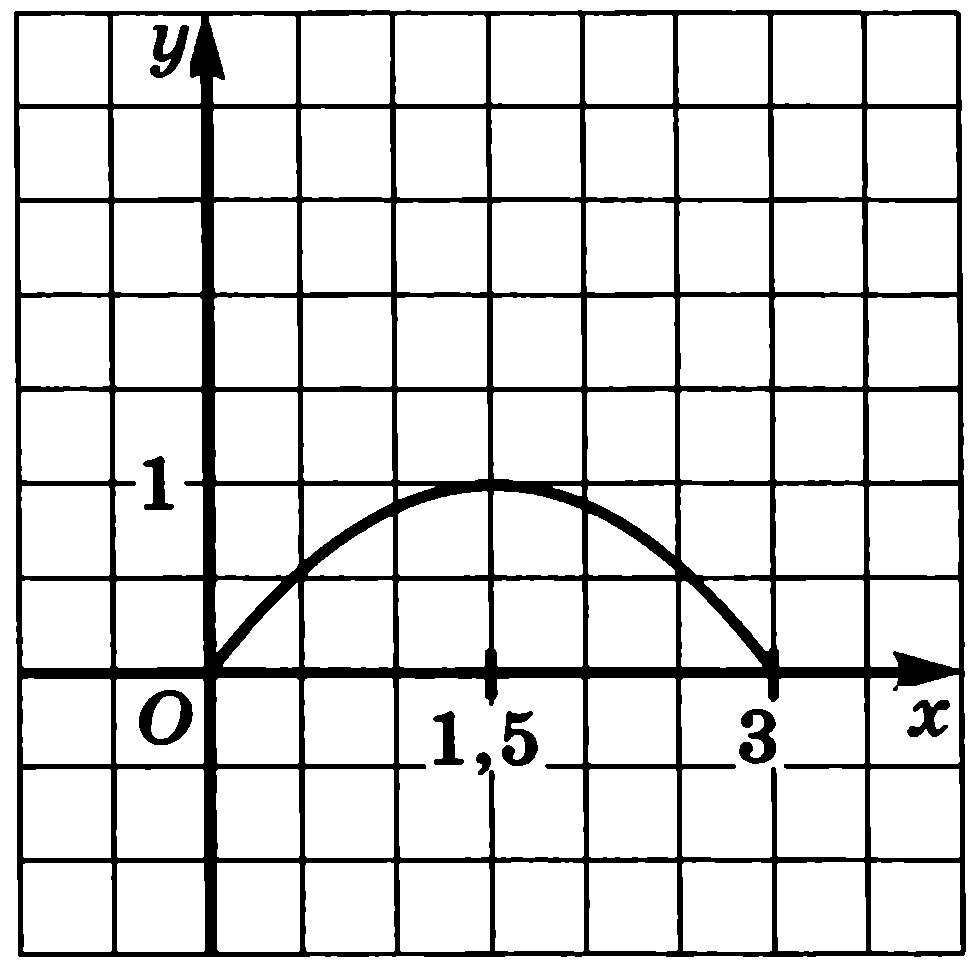2. На рисунке изображена часть графика периодической функции на отрезке [0; 3], длина которого равна периоду функции. Постройте график функции:

а) на отрезке [3; 6];

б) на отрезке [-3; 0];

в) на отрезке [6; 12];

г) на всей числовой прямой.

Решение:

а) на отрезке [3; 6];

б) на отрезке [-3; 0];

в) на отрезке [6; 12];

г) на всей числовой прямой.

3. Является ли число 32 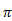периодом функции у = sin x, у = cos х?

_______________________

_______________________А основным периодом? _______________________________

4. Постройте график периодической функции у = f(x) с периодом Т = 2, если известно, что 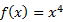на отрезке [-1; 1].

Решение:

5. Постройте график периодической функции у = f(x) с периодом Т = 4, если известно, что 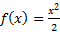на отрезке [-2; 2].

Решение:

6. Вычислите и запишите ответы:

sin 50,5 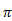=			sin390°=
sin 25,25 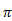=			sin540°=
sin 51,75 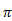=			cos750°=
sin 29,5 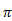=			cos930°=

Докажите тождество:

а) sin² (х - 8 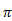) = 1 - cos² (16 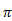- х)

б) cos² (4 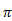+ х) = 1 - sin² (22 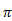- х).

Функция ,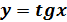

Её свойства и график.

I. Работа с учебником.

По соответствующему разделу учебника заполните следующие пункты.

Свойства функции тангенс:

1. Область определения. ______________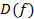

Периодичность.

Основной период функции 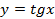равен ______________

Чётность, нечётность.

Функция тангенс является ___________________________

Доказательство:

4. Монотонность функции.Функция тангенс является возрастающей в интервале ___________________________ и убывающей в интервале ____________________________