Предпосылки МНК, методы их проверки

Исследования остатков e, предполагают проверку наличия следующих пяти предпосылок МНК:

• случайный характер остатков;

• нулевая средняя величина остатков, не зависящая от х;

• гомоскедастичность — дисперсия каждого отклонения e, одинакова для всех значений х;

• отсутствие автокорреляции остатков. Значения остатков eраспределены независимо друг от друга;

• остатки подчиняются нормальному распределению.

В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и по методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков e_i не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

Прежде всего, проверяется случайный характер остатков e_i,- первая предпосылка МНК.

С этой целью строится график зависимости остатков e,- от тео­ретических значений результативного признака.

Если на графике получена горизонтальная полоса, то остатки e представляют собой случайные величины и МНК оправдан, теоретические значения 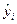хорошо аппроксимируют фактические значения у.

Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что 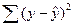= 0. Это выполнимо для линейных моделей н моделей, нелинейных относительно включаемых переменных. Для моделей, нелинейных по оцениваемым параметрам и приводимых к линейному виду логарифмированием, средняя ошибка равна нулю для логарифмов исходных данных.

Вместе с тем несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных остатков и величин х_i, что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным графиком зависимости остатков еот теоретических значений результативного признака у_х строится график зависимости случайных остатков eот факторов, включенных в регрессию х_i.

Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений х_i. Если же график показывает наличие зависимости e; то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора х_i. Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от х_i, например х², или преобразовать значения у. Скопление точек в определенных участках значений фактора х_i говорит о наличии систематической погрешности модели.

Корреляция случайных остатков с факторными признаками позволяет проводить корректировку модели, в частности использовать кусочно-линейные модели.

Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F. Вместе с тем оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки МНК.

Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок.

В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной.Это значит, что для каждого значения фактора х_i остатки e_i имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.

Гомоскедастичность остатков означает, что дисперсия остатков e_i одинакова для каждого значения х.

Наличие гетероскедастичности может в отдельных случаях привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок коэффициентов регрессии в основном зависит от соблюдения второй предпосылки МНК, т. е. независимости остатков и величин факторов. Гетероскедастичность будет сказываться на уменьшении эффективности оценок b_i. В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии, предполагаю­щей единую дисперсию остатков для любых значений фактора.

При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастичности может использоваться метод Гольдфельда - Квандта, разработанный в 1965 г. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение гомоскедастичности, они предложили параметрический тест, который включает в себя следующие шаги:

1. Упорядочение n наблюдений по мере возрастания переменной х.

2. Исключение из рассмотрения С центральных наблюдений; при этом (n — C): 2 > р, где р — число оцениваемых параметров

3. Разделение совокупности из (n - С) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.

4. Определение остаточной суммы квадратов для первой (S_i) и второй (S_j) групп и нахождение их отношения: R = S_i:S_j.

При выполнении нулевой гипотезы о гомоскедастичиссти отношение R будет удовлетворять F-критерию с (n - С - 2р): 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

При построении регрессионных моделей важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения остатков e_I распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между e_I и e_j, где e_I - остатки текущих наблюдений, e_j- остатки предыдущих (последующих) наблюдений

,

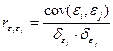т. е. по обычной формуле линейного коэффициента корреляции. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности F(e_i) зависит от i-й точки наблюдения и от распределения значений остатков в других точках наблюдения.

Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динамики, где ввиду наличия тенденции последующие уровни динамического ряда, как правило, зависят от своих предыдущих уровней.