Численное решение уравнения теплопроводности в табличном процессоре microsoft excel

При решении системы линейных алгебраических уравнений методом прогонки в табличном процессоре Microsoft Excel исходную систему проводим к виду, когда коэффициент в первом уравнении перед неизвестной равняется единице: 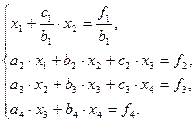(2.1)

Для этого разделим первое уравнение системы на коэффициент при первой неизвестной 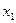. В столбцы таблицы Microsoft Excel записываем номера уравнений системы, значения свободных частей уравнений системы, значения свободных частей уравнений системы и коэффициенты перед элементами под главной диагональю, на главной диагонали и над главной диагональю матрицы коэффициентов системы. В следующих двух столбцах вычисляем значения вспомогательных коэффициентов 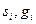. Последний в таблице столбец предназначается для вычисления решения системы 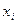. (Рис.2.1).

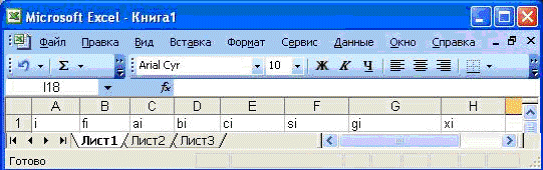
Рис. 2.1. Подготовка столбцов таблицы для вычислений методом прогонки.

Для численного решения уравнения теплопроводности потребуется многократное решение системы линейных алгебраических уравнений (1.18) методом прогонки. При этом ясно, что матрица коэффициентов перед неизвестными системы одинакова и ее элементы не зависят от значения пространственной и временной координат в узлах сетки. Из формул 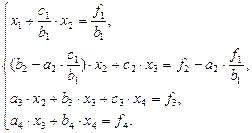(2.2)

следует, что и вспомогательные коэффициенты 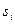также будут одинаковыми при решении всех систем. Эти коэффициенты вычислим один раз и далее будем на них только ссылаться в формулах. Поэтому для решения уравнения теплопроводности расположим исходные данные несколько в другом порядке: те величины, которые не будут меняться при разных расчетах, запишем в левых столбцах таблицы, а те, что при повторных расчетах меняются – в правых (рис. 2.2). Так что порядок столбцов в

решении примем следующий: в первый столбец заносим значения пространственной координаты, в которых вычисляется решение; во второй – номер уравнения; третий, четвертый, пятый столбцы будут занимать коэффициенты a, b, c уравнений системы; в шестом столбце будут располагаться вычисленные значения коэффициентов 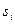; в седьмом столбце будем вычислять значения температуры в узловых точках 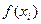в соответствии с начальными условиями задачи (1.11) (рис. 2.2).

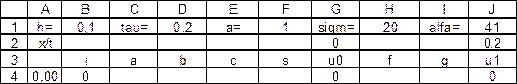
Рис. 2.2. Подготовка столбцов таблицы для решения уравнения теплопроводности

методом прогонки

На этом завершается подготовительная работа поиска решения. Все следующие столбцы таблицы будут содержать меняющиеся решения системы. Поэтому в следующих трех столбцах будем проводить вычисления тех величин, которые будут меняться при решении системы для следующего временного слоя: правая часть уравнений системы 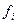, вспомогательные коэффициенты 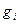и температура на следующем временном слое .

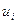Ø Формулы прямого хода для вычисления , :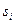

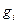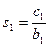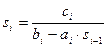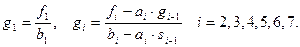, , (2.3)

Ø Рекуррентные соотношения – обратный ход метода прогонки для вычисления :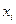

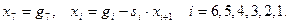(2.4)

Производим вычисление в первых столбцах таблицы, чтобы обеспечить наличие всех исходных данных для расчета (рис. 2.3, 2.4).

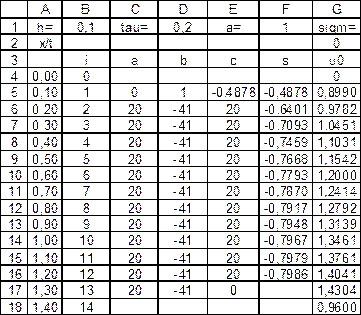
Рис. 2.3. Исходные данные расчета методом прогонки (режим отображения чисел)

Рис. 2.4. Исходные данные расчета методом прогонки (режим отображения формул)

Значения 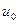и 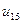вычисляются из краевых условий задачи (1.15) и (1.16), и заносятся в соответствующие ячейки таблицы. Значения температуры 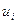в узлах нулевого временного слоя решения вычисляются из начальных условий (1.11).

Далее вычисляются значения свободного столбца системы (1.18) и вспомогательных коэффициентов по формулам (2.3) (рис. 2.5, 2.6). Все ссылки на ячейки с неизменяющимися в ходе расчета данными являются абсолютными для обеспечения их неизменности при дальнейшем копировании расчетных формул. Прямой ход метода прогонки завершен.

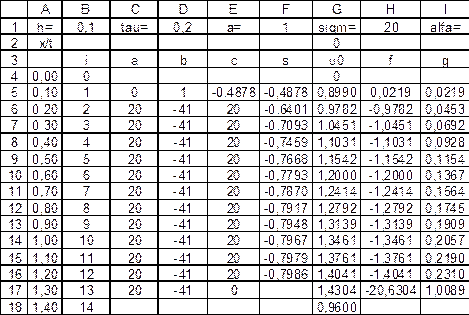
Рис. 2.5. Вычисление столбца свободных членов системы и вспомогательных коэффициентов для первого временного слоя (режим отображения чисел)

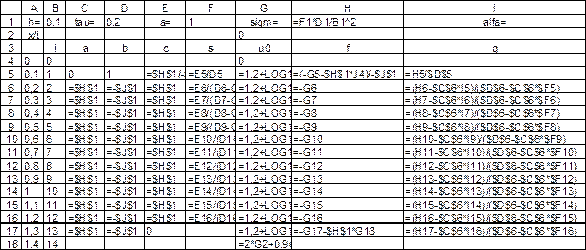
Рис. 2.6. Вычисление столбца свободных членов системы и вспомогательных коэффициентов 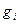для первого временного слоя (режим отображения формул)

Выполняя обратный ход метода прогонки, получим в соответствии с формулами (2.4) значения температуры на первом временнóм слое в столбце J таблицы (рис. 2.7, 2.8).

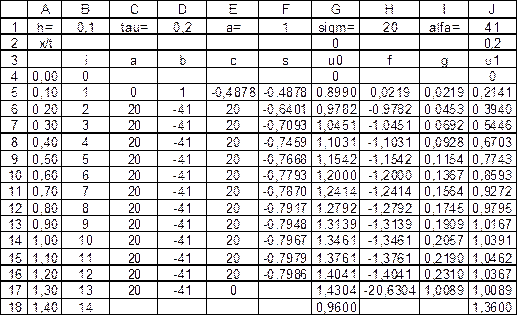
Рис. 2.7. Вычисление температуры на первом временном слое обратным ходом

метода прогонки (режим отображения чисел)

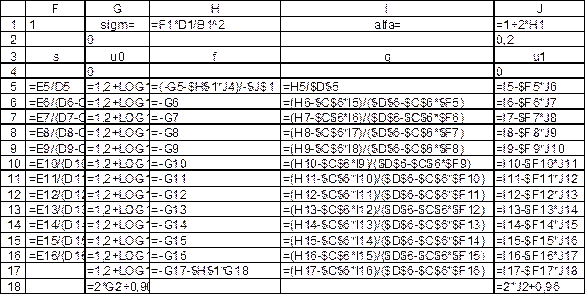
Рис. 2.8. Вычисление температуры на первом временном слое обратным ходом

метода прогонки (режим отображения формул)

Получили значение температуры на первом временнóм слое, т.е. при j=1. Для получения решения на втором временнóм слое j=2 нужно решить систему (1.18), свободный столбец которой содержит температуру первого слоя в узлах, т.е. полученные в столбце J величины. Следует повторить вычисление столбца свободных членов, вспомогательных коэффициентов gi и обратным ходом получить значения температуры в узлах для второго временного слоя. Значит, можно скопировать диапазон с вычислениями в этих трех столбцах, т.е. H5:J13 и вставить в следующие столбцы, т.е. столбцы K, L, M таблицы (рис. 2.9).

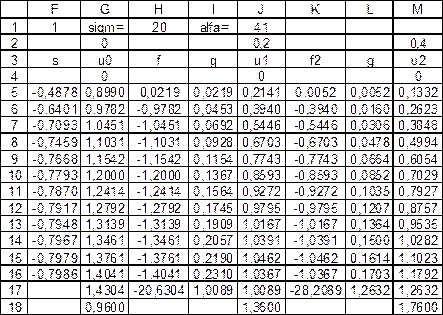
Рис. 2.9. Вычисление температуры на втором временном слое (режим отображения

чисел)

Как известно, при копировании формул в табличном процессоре Microsoft Excel адреса относительных ссылок меняются, что приведет к перерасчету по формулам с другими исходными данными, адреса абсолютных ссылок не изменяются, адреса смешанных ссылок меняются частично (рис. 2.10). Перед копированием нужно вписать граничные значения температуры в соответствии с граничными данными в ячейках J4 и J14 исходного задания.

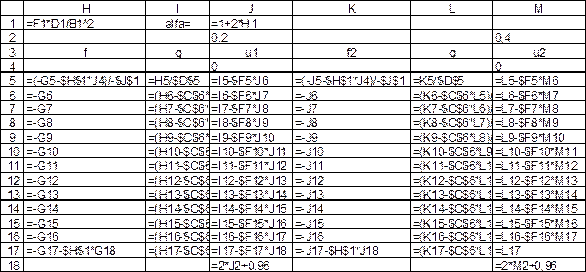
Рис. 2.10. Вычисление температуры на втором временном слое (режим отображения формул)

Продолжаем копирование и вставку диапазона таблицы с вычислением столбца свободных членов, вспомогательного коэффициента 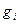и значения температуры на очередном временном слое до тех пор, пока не получим значения температуры на всем диапазоне изменения времени.

Полученные значения температуры сводим в единую таблицу (рис. 2.11).

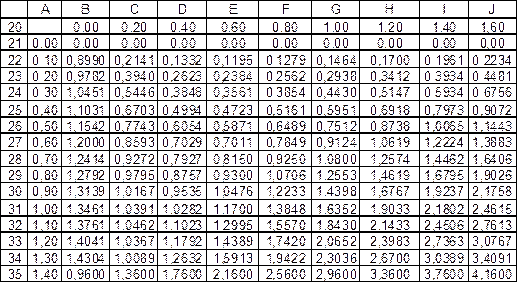
Рис. 2.11. Полученное решение

Строим графическое представление полученного решения (рис. 2.12). Полное решение приведено на рис. 2.13.

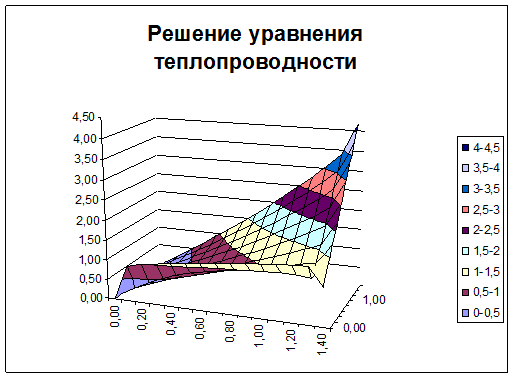
Рис. 2.12. Графическое представление решения уравнения теплопроводности

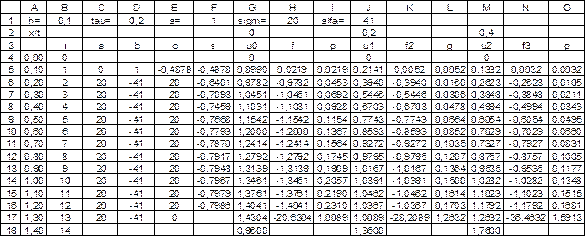
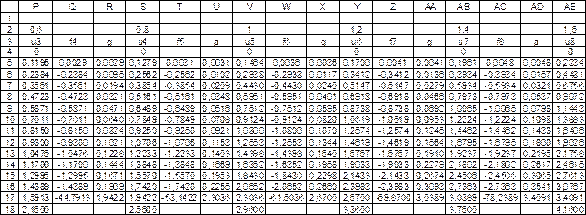
Рис. 2.13. Полное решение (режим отображения чисел)