Найдите наименьшее натуральное число, квадрат которого оканчивается на 2009

Нижегородская (VII открытая) городская математическая олимпиада школьников

г. Нижний Новгород, НФ ГУ-Высшая Школа Экономики, 13 декабря 2009 года

Вариант подготовлен Дмитрием Юрьевичем Кузнецовым (НФ ГУ ВШЭ, г.Н.Новгород). Председатель жюри – профессор НФ ГУ ВШЭ Валерий Александрович Калягин.

УСЛОВИЯ И ИДЕИ РЕШЕНИЙ ЗАДАЧ

Класс

1. Сколько трёхзначных чисел, делящихся на 3 и не содержащих в своей десятичной записи тройки?

Ответ: 216 чисел. Решение:Первой цифрой такого трёхзначного числа может быть любая из 8-и цифр, кроме 0 и 3, вторая – любая из 9-и цифр, кроме 3, а третья – любая из 3-х цифр, которая определяется по остатку при делении на 3 суммы двух первых цифр (если нужна цифра с остатком 0 – это 0, 6, 9; если с остатком 1 – это 1, 4, 7; если с остатком 2 – это 2, 5, 8). Тогда по правилу произведения в комбинаторике количество нужных нам чисел равно 8×9×3=216.

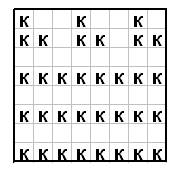
Дядька Черномор хочет показать своим богатырям-королевичам такую расстановку 33 королей на шахматной доске, что каждый король находится под защитой не более чем двух других королей (король защищает все соседние по стороне или вершине клетки). Есть ли у него такая возможность?

Ответ: есть, пример см. на рис.

3. Точка K вне равностороннего треугольника АВС такова, что угол AKB=60°, а точки К и С лежат по разные стороны от прямой АВ. Докажите, что биссектриса угла AKB проходит через центр О треугольника АВС (центр треугольника – это точка пересечения медиан).

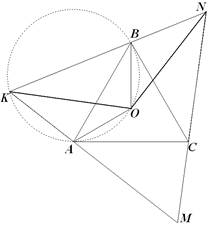Решение 1:Построим на продолжении луча КВ за точку В такую точку N, что BN=AK. ÐNBC=180°–60°–ÐABK=ÐKAB, значит, треугольники BCN и ABK равны по двум сторонам и углу между ними. Также равны углы КАО и NBO, отрезки АО и ВО, значит, равны также треугольники KAO и NBO. Следовательно, KO=NO, т.е. треугольник KON – равнобедренный. Из двух последних утверждений следует, что ÐBKO=ÐBNO=ÐAKO, значит, КО – биссектриса угла АКВ.

Комментарий:Фактическиречь идёт о двух равносторонних треугольниках, один из которых (АВС) вписан в другой (KNM) – см.чертёж. А у таких треугольников будет общий центр, который является и точкой пересечения медиан, высот, биссектрис, а также центром вписанной и описанной окружностей.

Решение 2:(очень простое решение, использующее знание свойств вписанных углов) Т.к. ÐАОВ=120°, ÐАКВ=60°, а их сумма равна 180°, то точки А, О, В и К лежат на одной окружности. Из равенства отрезков АО и ВО следует, что КО – биссектриса угла АКВ.

4. В квадрате 3´3 расставлены некоторым образом все целые числа от 1 до 9. Сначала подсчитали средние арифметические чисел в четырёх различных квадратах 2´2 (все они оказались целыми числами), а затем подсчитали среднее арифметическое полученных четырёх чисел (оно также оказалось целым). Какое наибольшее значение могло принимать последнее подсчитанное число?

Ответ:6 (см. пример таблицы на рисунке).

Доказательство оценки:Подсчёт последнего среднего арифметического даёт следующее значение 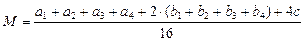, где a_i – числа в углах, b_j – числа в средних клетках на краю, с – число в центре таблицы. Тогда 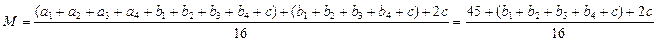и 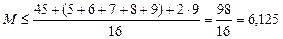, а наибольшее возможное целое значение равно 6.

Найдите наименьшее натуральное число, квадрат которого оканчивается на 2009.

Ответ: 1747. Решение: Пусть наше число равно N, тогда число (N²–9) оканчивается на 2000. Значит, (N²–9)=(N–3)(N+3) делится на 2000=2⁴×5³. Делиться на 5 может только один из двух множителей (N–3) и (N+3), т.к. их разность 6 не делится на 5. При этом оба множителя должны быть чётными, но одновременно не делящимися на 4, значит, один из них делится на 2, другой – на 2³=8. Таким образом, один из этих множителей делится на 2×5³=250, а ещё один – на 8, причём это может быть один и тот же множитель. Разобрав случаи для (N–3) и (N+3) чисел 250, 500, 750, 1000, 1250, 1500, 1750, обнаружим, что условия делимости выполняются для N равных 253, 747, 997, 1003, 1253, 1747. Первым из квадратов, оканчивающихся на 2009, будет 1747²=3052009.

Класс

1. Найдите все квадратные трехчлены ax²+bx+c, у которых сумма коэффициентов равна 0, а график соответствующей квадратичной функции симметричен относительно оси ординат.

Ответ: a(x²–1), где a – любое действительное ненулевое число. Решение:Сумма коэффициентов является значением квадратичной функции в точке 1, значит, x=1 является корнем данного квадратного трехчлена. В силу симметрии относительно оси ординат корнем является также x= –1, поэтому наш трехчлен имеет вид a(x–1)(x+1)=a(x²–1).

+	+	+	+
-	-	-		-3
+	+		+
-		-		-2
		–1

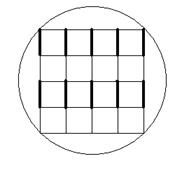
2. Во всех клетках таблицы 4´4 расставляются числа –1, 0 и 1. Какое наибольшее количество различных значений могут принимать 8 сумм чисел в строках и в столбцах?

Ответ: 8 различных значений, пример см. на рисунке, числа +1 и –1 отмечены знаками «+» и «-».

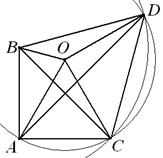3. В равнобедренном треугольнике ABC угол A равен 90°. D – точка пересечения биссектрисы угла A и окружности радиуса BC с центром в точке B. Найдите угол ОАВ, где О – центр описанной окружности треугольника ACD.(Задача предложена П.А.Суховым, 2 курс НФ ГУ ВШЭ)

Решение:Треугольники BAD и CAD равны, т.к. АВ=АС (катеты равнобедренного прямоугольного треугольника), АD – общая сторона и ÐBAD=ÐCAD. Значит, CD=BD=BC, т.е. треугольник BCD – равносторонний и ÐBCD=60°. Тогда ÐADC=180°–ÐDAC–ÐACD=180°–45°–(45°+60°)=30°. Т.к. центральный ÐАОС=2ÐADC=60° и ОА=ОС, то треугольник OAC – равносторонний, значит, ÐОАВ=ÐВАС–ÐОАС=90°–60°=30°.

4. Центр круга расположен в узле клетчатой сетки (сторона клетки равна 1). Какой наименьший радиус должен быть у круга, чтобы в накрытой им области можно было отметить 10 единичных отрезков (сторон клеток), не имеющих общих концов? 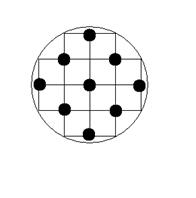(Задача предложена П.А.Суховым, 2 курс НФ ГУ ВШЭ)

Ответ: 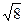. Решение: Кругом меньшего радиуса мы покроем целиком только единичные отрезки из области, не большей той, что показана на первом рисунке. Но в ней нельзя отметить нужные 10 отрезков, т.к. любая сторона содержит один из отмеченных узлов, а их всего 9. Для круга радиуса 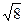пример приведён на втором рисунке.

5. Среди цифр натурального числа ровно один ноль, а при его вычёркивании число уменьшается в 9 раз. Найдите все такие числа.

Ответ: 405, 2025, 6075, 10125, 30375, 50625, 70875.Решение:Ноль в исходном числе не мог стоять на последнем месте, т.к. число после деления уменьшилось бы в 10 раз. Пусть после вычёркивания ноля получилось число a×10ⁿ+b, где n – количество цифр натурального числа b, стоящего после зачёркнутого ноля в исходном числе, a – натуральное число, стоящее перед зачёркнутым нолём. Тогда a×10ⁿ⁺¹+b=9(a×10ⁿ+b), откуда a×10ⁿ=8b, но b<10ⁿ, значит, a является натуральным однозначным числом (т.е. ненулевой цифрой), меньшим 8. Натуральное число 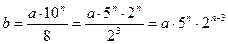не содержит ноля, а значит, не может и оканчиваться на ноль, откуда получаем, что n£3. Перебор всех возможных случаев ненулевой цифры a£7(при условии, что 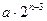является нечётным числом) даст для числа b следующие варианты: при n=1: 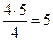, при n=2: 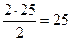, , 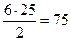при n=3: 1×125=125, 3×125=375, 5×125=625, 7×125=875. Получаем следующие случаи – 405:9=45, 2025:9=225, 6075:9=675, 10125:9=1125, 30375:9=3375, 50625:9=5625, 70875:9=7875.

Класс

1. Существует ли геометрическая прогрессия a, b, c такая, что квадратный трехчлен ax²+bx+c имеет действительные корни?

Ответ: не существует. Решение: Заметим, что из свойств геометрической прогрессии следует, что b²=ac, тогда дискриминант данного квадратного трехчлена D=b²–4ac= –3b²£0. При этом действительные корни могут быть только при D³0, значит, b=0, что невозможно для геометрической прогрессии.

2. Расставьте в клетках таблицы 10´10 цифры так, чтобы в каждом столбце и в каждой строке встречались все цифры от 0 до 9, а в любом прямоугольнике 2´5 (и горизонтально, и вертикально размещённом) сумма цифр была одна и та же.

Пример: см. таблицу справа.

Комментарий:Догадаться до расстановки можно следующим образом. Применим диагональную раскраску в 10 цветов-цифр, тогда в силу симметрии относительно главной диагонали достаточно рассмотреть только горизонтально размещённые прямоугольники 2´5. Теперь найдём такую перестановку цифр, в которой суммы пар соседних цифр циклически повторяются, при этом длина периода равна 5 (например, 2, 9, 1, 8, 0, 7, 4, 6, 3, 5; а в парах суммы равны соответственно 11, 10, 9, 8, 7, 11, 10, 9, 8, 7). В результате в любом прямоугольнике 2´5 будут присутствовать 5 пар-доминошек с суммами 11, 10, 9, 8 и 7, при этом в каждом таком прямоугольнике сумма всегда будет равна 11+10+9+8=7=45, что и необходимо для выполнения требуемого условия.