III. Конкуренция двух фирм
Общий случай
Рассмотрим две фирмы, производящие взаимозаменяемые товары одинакового качества и находящиеся в одной рыночной нише. Последнее означает, что у потребителей в этой нише нет априорных предпочтений и они приобретут тот или иной товар, не обращая внимания на знак фирмы.
В этом случае, на рынке устанавливается единая цена,которая определяется балансом суммарного предложения и спроса. Иными словами, в рамках нашей модели конкурентная борьба ведётся только рыночными методами. То есть, конкуренты могут влиять на противника путем изменения параметров своего производства: себестоимость, время цикла, но не могут прямо вмешиваться в ситуацию на рынке («назначать» цену или влиять на потребителей каким либо иным способом.)
Уравнения динамики оборотных средств запишем по аналогии с (2) в виде
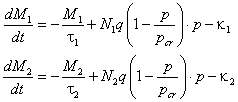 , , | (17) |
где использованы те же обозначения, а индексы 1 и 2относятся к первой и второй фирме, соответственно. Величины N1 и N2– числа потребителей, приобретших товар первой и второй фирмы. В отсутствии постоянных затрат (κ1 = κ2 = 0) эта модель по форме совпадает с моделями [9,10,11]. Близкая модель, с учетом постоянных затрат, рассмотрена в [13].
Учтем, что товарный баланс устанавливается быстро, то есть, произведенный каждой фирмой товар не накапливается, а реализуется по ценеp. Тогда
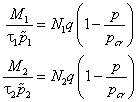 , , | (18) |
где p̃1и p̃2 –себестоимости товаров в первой и второй фирме.
С учетом (18) представим (17) в виде
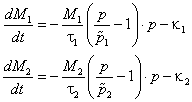 . . | (19) |
Уравнение для цены, по аналогии с (3),
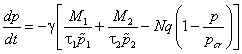 . . | (20) |
Считая, как и выше, что ценовое равновесие устанавливается быстро, получим:
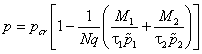 . . | (21) |
Подставив (21) в (19) имеем:
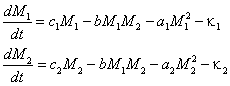 , , | (22) |
где
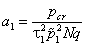 , , 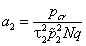 , , 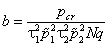 , , 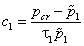 , , 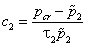 . . | (23) |
Исследуем систему (22) в случае, когда постоянные издержки (κ1, κ2) пренебрежимо малы. Для этого представим её в виде
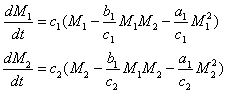 . . | (24) |
Модель (24) хорошо известна, и по форме совпадает с моделью борьбы условных информаций [9,10].В работе [11] она использовалась для описания конкуренции фирм за рынок, и в качестве динамических переменных в ней фигурировали числа потребителей, предпочитающих товары той или иной фирмы.
В нашем случае динамическими переменными являются оборотные средства M1 и M2. Это накладывает ограничение на параметры модели. Из (23) следует:
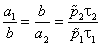 . . | (25) |
Фазовые портреты системы (24) представлены на рис. 1а в случае τ1p̃1 < p̃2τ2,и на рис. 1б в случае τ1p̃1 > p̃2τ2.В обоих случаях главные изоклины в соотношении (25) представляют собой параллельные прямые, и их угол наклона ϕ таков, что
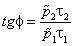 . . |
Это означает, что стационарные состояния в системе(24) отсутствуют.
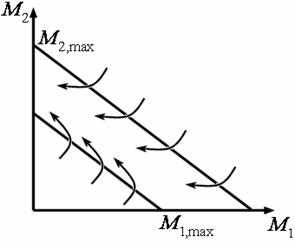 а а | 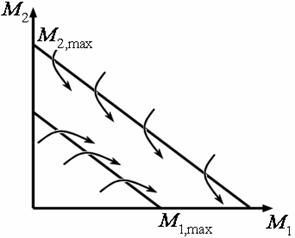 б б |
| Рис. 1. Фазовый портрет системы (24) (без учёта постоянных издержек) | |
| а – случай τ1p̃1 < p̃2τ2. б – случай τ1p̃1 > p̃2τ2. |
При τ2p̃2 < p̃1τ1изоклина горизонталей (то есть, линия, на которой 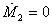 ) расположена выше изоклины вертикалей (где
) расположена выше изоклины вертикалей (где 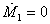 ).В этом случае система при любых начальных условиях попадает в область между изоклинами, где M2 неограниченно возрастает, а M1 – убывает. Выйти из положительного квадранта величина M1не может, поскольку в модели (24) ордината (M1 = 0) является изоклиной вертикалей. Реально условие M1 = 0 означает, что первая фирма терпит банкротство. Тогда в силу вступает модель (6), в рамках которой вторая фирма стремится к устойчивому состоянию
).В этом случае система при любых начальных условиях попадает в область между изоклинами, где M2 неограниченно возрастает, а M1 – убывает. Выйти из положительного квадранта величина M1не может, поскольку в модели (24) ордината (M1 = 0) является изоклиной вертикалей. Реально условие M1 = 0 означает, что первая фирма терпит банкротство. Тогда в силу вступает модель (6), в рамках которой вторая фирма стремится к устойчивому состоянию 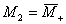 в уравнении (9), которое совпадает с величиной
в уравнении (9), которое совпадает с величиной
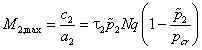 . . |
При p̃2 > p̃1 (рис. 1б)ситуация аналогична, но крах терпит вторая фирма, а первая стремится к устойчивому состоянию
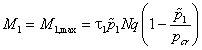 . . |
При p̃2 = p̃1и τ2 = τ1 изоклины сливаются. Это означает, что возможно существование фирм при различных значениях M1и M2, но эти состояния при малых изменениях параметров сдвигаются вдоль линии вплоть, до полного вытеснения одного другим.
Отметим: аналогичная ситуация имеет место в биологии,именно в задаче о борьбе двух сходных видов за одну экологическую нишу, если единственным фактором конкуренции является потребление общего ресурса.Соотношение (25) является ограничением именно этого обстоятельства. Отсутствие стационарных состояний или образование их континуума означает, что система (24)с учетом (25) не груба (в смысле Андронова) или, что то же, структурно неустойчива.
В свете этого, рассмотрим полную систему (22) при условиях
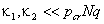 . . | (26) |
Фазовые портреты представлены на рис. 2а и 2б. Изоклина вертикалей в модели (22) ( 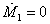 )имеет вид:
)имеет вид:
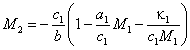 . . | (27) |
Она располагается несколько ниже изоклины вертикалей модели (24) и существенно отклоняется от неё при M1 ≤ κ1/c1 << M1,max.
 а а | 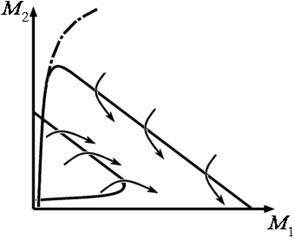 б б |
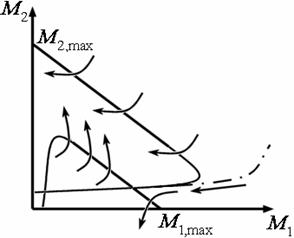
| Рис. 2. Фазовый портрет полной системы (22) (с учётом постоянных издержек) | |
| а – случай p̃1 < p̃2. б – случай p̃1 > p̃2. |
Изоклина горизонталей ( 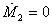 ) имеет вид
) имеет вид
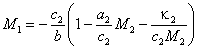 . . | (28) |
Она также близка к изоклине горизонталей в (24), но отклоняется от неё при M2 ≤ κ2/c2 << M2,max.
При p̃1 < p̃2 (рис. 2а) картина близка к рис. 1а, но имеются отличия.
Во-первых, модель (22) допускает выход из положительного квадранта, где M1 (или M2) формально становится отрицательным. Реально, это означает, что при M1 ≤ 0 первая фирма терпит банкротство и уходит с рынка. Оставшаяся на рынке фирма описывается уравнением (6) и стремится к устойчивому состоянию 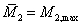 .
.
Во вторых, возникают два стационарных состояния.
Одно из них, при малых значениях M1и M2:
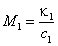 , , 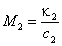 , , |
представляет собой неустойчивый узел и близко к состоянию 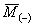 в модели (6).
в модели (6).
Второе состояние при
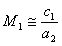 , , 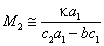 | (29) |
представляет собой седло. Через него проходит сепаратриса,разделяющая области притяжения двух устойчивых состояний: M1 < 0, M2 = M2,maxи M2 < 0, M1 = M1,max (представлена на рис. 2а штрих пунктиром). Из рисунка видно, что ареал притяжения второй фирмы существенно больше, чем первой. Тем не менее, даже при неблагоприятных для первой фирмы условиях, когда себестоимость товара в ней больше, чем во второй, возможно всё же вытеснение второй фирмы.Это может иметь место, если в начальный момент её оборотные средства существенно больше, чем во второй фирме.
При p̃1 > p̃2 ситуация аналогична, но большим ареалом притяжения обладает состояние M1 = M1,max(см. рис. 2б).
При p̃2 ≅ p̃1седло расположено в середине квадранта и области притяжения стационарных состояний одного порядка. В этом случае также происходит полное вытеснение одной из фирм, какой именно – зависит от начальных условий.
Важно, что во всех случаях происходит полное вытеснение одной из фирм. Устойчивое существование конкурентов в рамках модели(22) невозможно.
Модель (22) является структурно устойчивой (грубой в смысле Андронова). Малые изменения структуры модели (её параметров, и/или учет дополнительных малых факторов) не могут изменить её качественные результаты.
Таким образом, устойчивое сосуществование конкурентов возможно, только если в борьбе используются методы, выходящие за рамки чисто рыночных отношений.
Симметричный случай
В этом случае параметры фирм одинаковы. Это значит,что в уравнении (24) c1 = c2 = c; a1 = a2 = a,и, кроме того, a = b. Параметр c определяет масштаб времени; удобно выбрать естественный масштаб, то есть, в безразмерном времени t' = ctили, что то же, положить: с = 1.
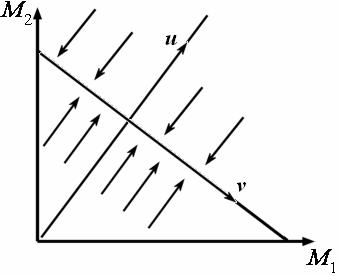 |
| Рис. 3. Фазовый портрет системы (30) (случай полной симметрии) |
Тогда модель (24) можно представить в виде
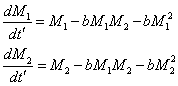 . . | (30) |
Фазовый портрет системы (30) представлен на рис. 3.В этом случае главные изоклины сливаются, и угол ϕ их наклона таков, что tg ϕ = 1.
Здесь удобно перейти к переменным
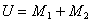 , , 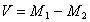 . . |
Из уравнений (30) нетрудно получить:
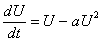 , , | (а) | (31) |
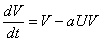 | (б) |
Из (31а) следует, что величина U(независимо от V) быстро (в меру t' ≈ 1, t = 1/c)стремится к устойчивому стационарному значению 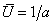 . Подставив его в (31б),получим
. Подставив его в (31б),получим
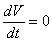 . . | (32) |
Это значит, что на линии изоклин
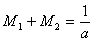 . . | (33) |
расположен континуум безразличных равновесий. В каждом из них одно из чисел Ляпунова равно нулю. Таким образом, симметричная модель не груба и сторонние (случайные) воздействия могут играть существенную роль. В нашем случае этот фактор можно учесть, записав уравнение Ланжевена для переменнойV:
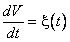 , , | (34) |
где ξ(t) – нормальный (гауссов), δ-коррелированный шум. Уравнение (34)описывает хорошо известный процесс – броуновский дрейф вдоль линии 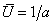 . Конечный результат дрейфа тоже хорошо известен: величина Vупирается в значения: либо V = M1(M2 = 0), либо V = –M2 (M1 = 0).
. Конечный результат дрейфа тоже хорошо известен: величина Vупирается в значения: либо V = M1(M2 = 0), либо V = –M2 (M1 = 0).
Таким образом, и в этом случае происходит полное вытеснение одного конкурента другим, даже если они полностью равноправны (что соответствует принципу Оруэлла: «All animals are equal, but some of them are more equal than others»).
Учтём в симметричной модели постоянные затраты.Уравнения (3) примут вид
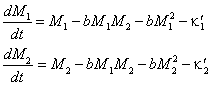 , , | (35) |
где κ1' = κ1/c << 1, κ2' = κ2/c << 1.
Фазовый портрет системы (35) представлен на рис. 4.Видно, что возникает стационарное состояние при
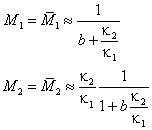 . . |
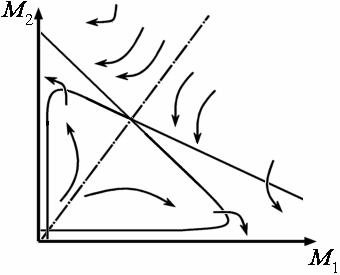 |
| Рис. 4. Фазовый портрет системы (35) (с учётом постоянных издержек) |
Это состояние неустойчиво (седло), через него проходит сепаратриса, разделяющая фазовое пространство на две области притяжения. В каждой из них один из конкурентов полностью вытесняет другого.
Учёт шумов размывает сепаратрису и приводит к дрейфу,в результате которого один из конкурентов полностью вытесняет другого. Таким образом, учёт постоянных затрат качественно не изменит ситуацию.
Учтём в рамках симметричной модели эффект рекламы.Цель её – привлечение потребителей к приобретению товаров данной фирмы (но не её конкурента) и дополнительные доходы связаны именно с этим эффектом. Как упоминалось, эффект рекламы выходит за рамки чисто экономических. Поэтому мы оценим его, используя дополнительные предположения.
В результате рекламы фирмы получают дополнительные доходы: δ1M1и δ2M2, соответственно.Примем, что эффект относительно мал (δ1, δ2 ≤ 1), но тем не менее, учет его важен, поскольку симметричная модель не груба.
Из предпринимательской практики известно, что расходы на рекламу R1и R2 зависят от доходов: δ1M1и δ2M2, причем, не линейно, а в более высокой степени.
Примем, что расходы растут квадратично, то есть
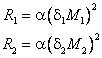 , , | (36) |
где α –феноменологический коэффициент. В оптимальном режиме работы предприятия сумма
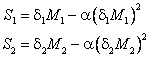 | (37) |
должна быть максимальна. Это имеет место при δ1M1 = α/2, и тогда обе суммы равны
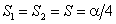 . . |
Фактически, это означает, что фирма, благодаря рекламе,обеспечивает постоянный (не зависящий от оборотных средств) доход. Модель (35)можно представить в виде:
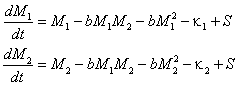 . . | (38) |
В случае S < κ1 и S < κ2качественные свойства модели не меняются. Фазовый портрет соответствует рис. 2,и всё сказанное выше остается в силе.
В случае S > κ1 и S > κ2ситуация меняется. Фазовый портрет представлен на рис. 5. Видно, что имеется устойчивое стационарное состояние при
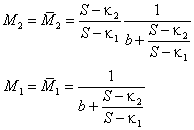 . . |
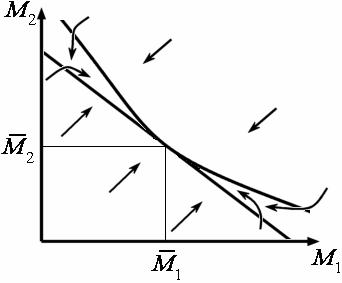 |
| Рис. 5. Фазовый портрет системы (38) (с учётом эффекта рекламы) |
| См. пояснения в тексте. |
Таким образом, в этом случае возможно сосуществование конкурентов. Смысл этого: просто, благодаря рекламе, каждая из фирм создаёт свою нишу, в которой потребители предпочитают приобретать товар именно этой фирмы. Фактически, конкуренты сосуществуют независимо.
