Стохастический процесс Тейла и Вейджа
Г. Тейл и С. Вейдж в целях дальнейшего изучения свойств адаптивных моделей предложили применить двухпараметрический предиктор Хольта (3.11) для прогнозирования некоторого вероятностного процесса, характеризующегося стохастическим трендом. Они вывели выражения для определения оптимальных параметров адаптации, минимизирующих средний квадрат ошибки прогнозирования.
Процесс Тейла—Вейджа аналитически записывается как:
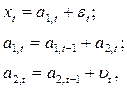
где a1,t — значение уровня исследуемого временного ряда xt в момент t;
a2,t— прирост уровня от момента t—1 к моменту t
εt , υt — временные последовательности с нулевым математическим ожиданием, постоянными дисперсиями и отсутствием ковариации, т. е.
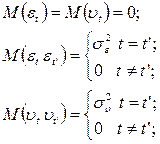
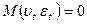 для любой пары (t, t’).
для любой пары (t, t’).
Временной ряд xt не является стационарным и не имеет строго определенной автоковариационной функции. Вторые же разности этого ряда имеют вполне определенную автоковариационную функцию
Схема составления прогноза в соответствии с (3.11) выглядит следующим образом:
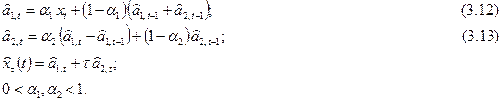
Если ошибку прогноза, сделанного в момент t на 1 шаг вперед, обозначить через e1(t), то уравнения адаптации (3.12) и (3.13) можно записать в виде:
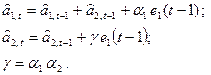
Ошибка прогноза:
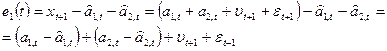
Следовательно, ошибка прогноза является суммой трех компонент: ошибки оценки уровня процесса в момент t, ошибки оценки прироста уровня в момент t и комбинации случайных компонент υ и ε в момент t + 1.
Сезонные модели
В экономике многие явления характеризуются периодически повторяющимися сезонными эффектами. Соответственно временные ряды, их отражающие, содержат периодические сезонные колебания. Эти ряды и их колебания можно представить как генерируемые моделями двух основных типов: моделями с мультипликативными и с аддитивными коэффициентами сезонности.
Модели первого типа имеют вид:
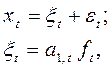
где динамика величины a1,t характеризует тенденцию развития процесса;
ft , ft-1, ft-l+1 - коэффициенты сезонности;
l — количество фаз в полном сезонном цикле (если ряд представляет месячные наблюдения, то в экономике обычно l =12, при квартальных данных l = 4 и т. п.);
εt — неавтокоррелированный шум с нулевым математическим ожиданием.
Модели второго типа записываются как:
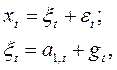
где величина a1,t описывает тенденцию развития процесса;
gt , gt-1, gt-l+1 - аддитивные коэффициенты сезонности;
l — количество фаз в полном сезонном цикле;
εt — неавтокоррелированный шум с нулевым математическим ожиданием.
Адаптивная модель с мультипликативной сезонностью была предложена П. Р. Уинтерсом. Аддитивная модель рассмотрена Г. Тейлом и С. Вейджем.
