Математические модели в экономике

Функции, используемые в экономике:

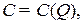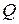а) издержки производства где — объём продукции;

б) функции спроса 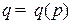и предложения 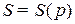, где 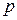— цена единицы товара; равновесная цена 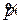находится из уравнения ;

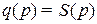в) производственная функция 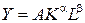, где 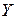— объём выпускаемой продукции, 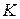— капитал, 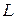— труд, .

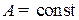Экономические приложения производной:

1) Предельная(маржинальная) величина функции 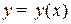— скорость изменения, т. е. производная функции 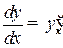(например, 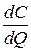— предельные издержки производства).

2) Темп функции 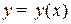— величина (обозначается 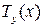), равная лога­рифмической производной данной функции, т. е. .

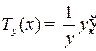3) Эластичность функции 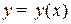(обозначается 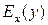) — произведение переменной 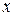на темп этой функции, т. е. 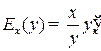(например, эластич­ность по спросу 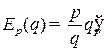, эластичность по предложению ).

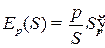4) Коэффициент эластичности 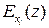функции нескольких переменных 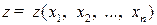по переменной 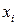— произведение этой переменной на темп изменения функции по данной переменной, т. е. 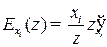(напри­мер, для производственной функции 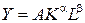коэффициент эластичности по капиталу равен 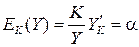, по труду — ).

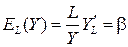Элементы теории игр

Пусть 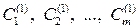—возможные стратегии 1-го игрока, 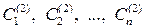—возможные стратегии 2-го игрока, 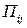—выигрыш 1-го игрока при выборе им 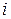-й стратегии 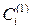, а 2-м игроком — 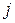-й стратегии .

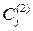Платёжная матрица: .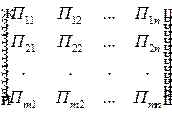

Нижняя цена игры — максимум из минимумов по строкам платёжной матрицы:

.

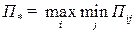Верхняя цена игры — минимум из максимумов по столбцам платёжной матрицы:

.

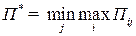Игра с «природой»:Пусть 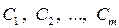— возможные стратегии игрока,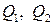— возможные стратегии «природы», 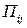—выигрыш игрока при выборе им 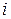-й стратегии 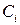, в то время как «природой» выбрана стратегия 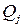с вероятностью .

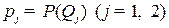Матрица выигрышей в игре с «природой»:

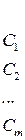
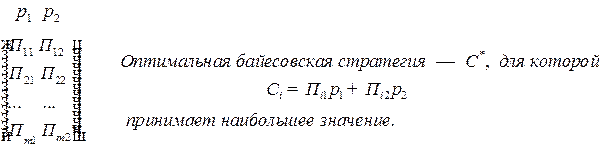
ЛИТЕРАТУРА

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. — М.: Высш. шк., 1998. — 320 с.

2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и анали­ти­ческой геометрии. — Ростов н/Д: Феникс, 1997. — 284 с.

3. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчи­с­ления. — Ростов н/Д: Феникс, 1997. — 431 с.

4. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. — Ростов н/Д: Феникс, 1997. — 512 с.

5. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. — М.: Наука, 1998. — 656 с.

6. Мантуров О.В., Матвеев Н.М. Курс высшей математики. Линейная алгебра. Аналитическая геометрия. Дифференциальное исчисление. — М.: Высш. шк., 1986. — 288 с.

7. Мантуров О.В. Курс вышей математики. Ряды. Уравнения матема­тической физики. Теория функций комплексной переменной. Численные методы. Теория вероятностей. — М.: Высш. шк., 1991. — 448 с.

8. Пискунов Н.С. Дифференциальное и интегральное исчисление (для ВТУЗов), Т.1. — М.: Наука, 1985. — 432 с.

9. Пискунов Н.С. Дифференциальное и интегральное исчисление (для ВТУЗов), Т.2. — М.: Наука. 1985. — 560 с.

10. Шипачёв В.С. Высшая математика. — М.: Высш. шк., 2000. — 480 с.

11. Гмурман В.Е. Теория вероятностей и математическая статистика. — М.: Высш. шк., 2003. — 497 с.

12. Смирнов В.Н. Курс теории вероятностей и математической статистики. — М.: Наука, 1969. — 353 с.

13. Яблонский С.В. Введение в дискретную математику. — М.: Высш. шк., 2003. — 384 с.

14. Математическая статистика. Учеб. для вузов / Горяинов В.Б., Павлов И.В., Цветкова Г.М., Тескин / Под ред. В.С. Зарубина, А.П. Крищенко). — М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. — 424 с.

15. Калинина В.Н., Панкин В.Ф. Математическая статистика. — М.: Высш. шк., 2002. — 336 с.

16. Баврин И.И. Высшая математика. — М.: ACADEMIA, 2002. — 616 с.

17. Высшая математика для экономистов (под редакцией проф. Н.Ш. Кремера). — М.: ЮНИТИ, 2003. — 471 с.

18. Кремер Н.Ш. Теория вероятностей и математическая статистика. — М.: ЮНИТИ, 2000. — 543 с.

Учебно-методическое издание

Составители:

СОБОЛЕВ Вадим Владимирович

НУРУТДИНОВА Инна Николаевна

СПРАВОЧНЫЙ МАТЕРИАЛ