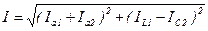Передаточные АЧХ и ФЧХ в цепях первого порядка
Отношение комплексного входного напряжения к комплексному входному току называют комплексным коэффициентом передачи 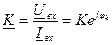
Зависимость модуля комплексного коэффициента передачи от частоты называется передаточная АЧХ, 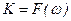 - передаточная АЧХ.
- передаточная АЧХ.
Зависимость аргумента комплексного коэффициента передачи от частоты называется передаточная ФЧХ, 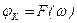 - передаточная ФЧХ.
- передаточная ФЧХ.
Модуль коэффициента передачи изменяется от 0 до 1.
Передаточные характеристики цепи RL
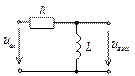 Выведем формулы передаточных АЧХ и ФЧХ цепи RL. Комплексный коэффициент передачи
Выведем формулы передаточных АЧХ и ФЧХ цепи RL. Комплексный коэффициент передачи 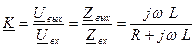
Домножим числитель и знаменатель на комплексно сопряженное число знаменателю.
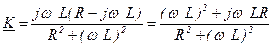
Выделим отдельно действительную и мнимую часть 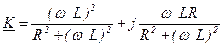
Разделим числитель и знаменатель на 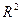
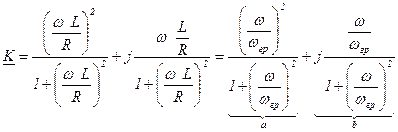
Воспользовавшись формулой 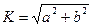 получим передаточную АЧХ цепи RL
получим передаточную АЧХ цепи RL
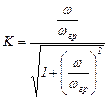 - передаточная АЧХ цепи RL
- передаточная АЧХ цепи RL
Передаточную ФЧХ получаем по формуле: 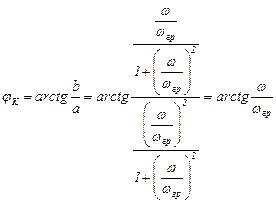
Зададимся несколькими частотами, чтобы построить передаточные характеристики.
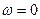
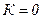
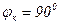
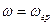
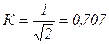
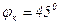
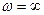
Вывод:
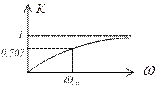
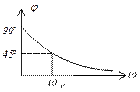
1) передаточная АЧХ в цепи RL зависит от того какой элемент стоит на выходе.
2) передаточная ФЧХ имеет линейный участок на частотах от 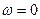 до
до 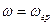 .
.
Передаточные характеристики цепи RС
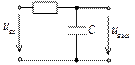 Выведем формулы передаточных АЧХ и ФЧХ цепи RL. Комплексный коэффициент передачи
Выведем формулы передаточных АЧХ и ФЧХ цепи RL. Комплексный коэффициент передачи 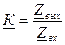
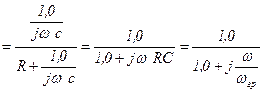 , где
, где 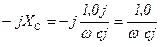 .
.
Домножим числитель и знаменатель на комплексно сопряженное число знаменателю.
Выделим отдельно действительную и мнимую часть
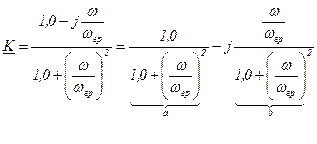
Воспользовавшись формулой 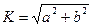 получим передаточную АЧХ цепи RС
получим передаточную АЧХ цепи RС
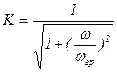 - передаточная АЧХ цепи RС
- передаточная АЧХ цепи RС
Передаточную ФЧХ получаем по формуле: 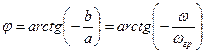
Зададимся несколькими частотами, чтобы построить передаточные характеристики.
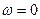
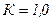
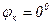
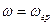
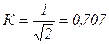
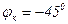
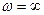
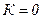
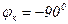
АЧХ ФЧХ

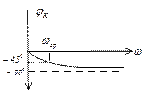
Вывод:
1) цепи RC передаточная АЧХ зависит от того, какой элемент стоит на выходе.
2) передаточная ФЧХ имеет линейный участок на частотах от 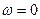 до
до 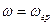 .
.
Тестовые задания:
| Задание | Слова для вставки |
| Вставьте пропущенные в определениях слова,взяв их из столбца «Слова для вставки» /одно слово – три точки/: 1).Входная АЧХ –это зависимость ... комплексного ... ... от ... . 2).Входная ФЧХ –это зависимость ... ... входного ... от ... . 3).Передаточная АЧХ –это зависимость ... комплексного ... ... от ... . 4).Передаточная ФЧХ –это зависимость ... ... коэффициента ... от ... . | модуль, сопротивление, входной, комплексный, частота, коэффициент передачи, аргумент |
Неразветвленная цепь RLC при гармоническом воздействии
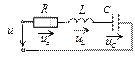 Пусть по цепи течет ток
Пусть по цепи течет ток 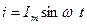 . Запишем уравнения мгновенных значений напряжений на каждом элементе
. Запишем уравнения мгновенных значений напряжений на каждом элементе
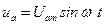
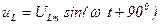
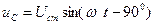
Общее напряжение равно сумме напряжений отдельных участков (справедливо для мгновенных значений и векторов) 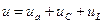 .
.
Построим векторную диаграмму для случая 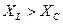
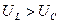
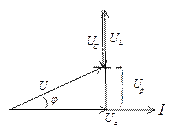
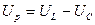 - реактивная составляющая напряжения.
- реактивная составляющая напряжения.
Выведем закон Ома для цепи RLC
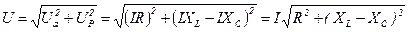
Обозначим 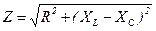 полное сопротивление цепи RLC и получим закон Ома для цепи RLC
полное сопротивление цепи RLC и получим закон Ома для цепи RLC 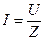
Разделим все стороны диаграммы напряжений на ток и получим диаграмму сопротивлений
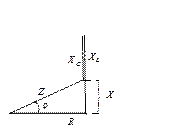 Обозначим
Обозначим 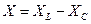 - реактивное сопротивление цепи.
- реактивное сопротивление цепи.
Если 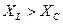
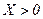 сопротивление цепи носит индуктивный характер,
сопротивление цепи носит индуктивный характер,
если 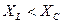
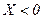 сопротивление цепи носит емкостной характер
сопротивление цепи носит емкостной характер
Умножим все стороны диаграммы напряжений на I и получим диаграмму мощностей
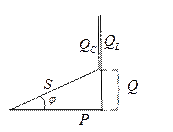 Обозначим
Обозначим 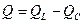 реактивная мощность цепи
реактивная мощность цепи
Построим диаграммы для случая 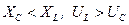
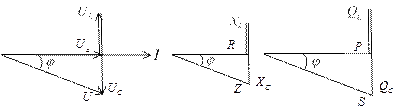
Пример решения задачи
Дано:
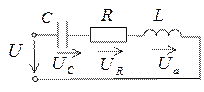
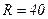 Ом
Ом
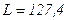 мГн
мГн
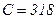 мкФ
мкФ
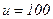 В
В
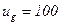 В
В
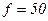 Гц
Гц
Найти: 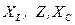
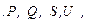
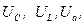
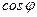
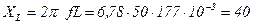 Ом
Ом
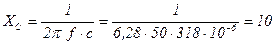 Ом
Ом
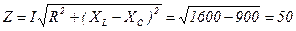 Ом
Ом
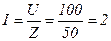 А
А
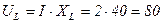 В
В 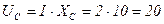 В
В
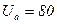 В
В
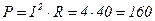 Вт
Вт 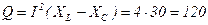 вар
вар
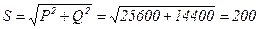 ВА
ВА
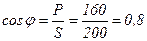
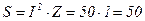 Вт
Вт
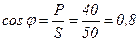
Тестовые задания:
| Задание | Варианты ответов | ||
| 1.Укажите какое из математических выражений не относится к цепи последовательного соединения RLC. | а) 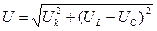 ; б) ; б) 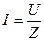 ; в) ; в) 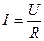 ; г) ; г) 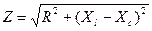 | ||
| Задание | Варианты ответов | ||
| 2.Укажите какое из приведенных математических выражений является законом Ома для цепи RLC. | а) 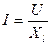 ; б) ; б) 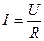 ; г) ; г) 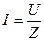 ; д) ; д) 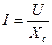 . . | ||
| Задание | Векторная диаграмма | Варианты ответов | |
| 3.Укажите какой вектор на векторной диаграмме соответствует перечисленным в ответах напряжениям. | 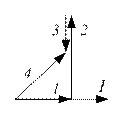 | а) напряжение на катушке; индуктивности б) напряжение на резисторе; в) напряжение на конденсаторе; г) общее напряжение цепи. | |
Параллельные цепи RL и RC при гармоническом
 воздействии
воздействии
Если цепь параллельна, то векторную диаграмму начинают строить с вектора напряжений, т.к. напряжение участков при параллельном соединении одинаково.
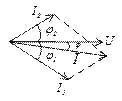
Ток 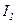 отстает от напряжения на угол
отстает от напряжения на угол 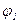 (цепь RL), ток
(цепь RL), ток 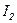 опережает напряжение на угол
опережает напряжение на угол 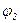 (цепь RC). Общий ток равен векторной сумме этих токов. Из диаграммы видно, что найти общий ток можно только специальным методом расчета. Этот метод называется метод составляющих токов. Построим подробную векторную диаграмму этой цепи. Строим вектор напряжений и токи
(цепь RC). Общий ток равен векторной сумме этих токов. Из диаграммы видно, что найти общий ток можно только специальным методом расчета. Этот метод называется метод составляющих токов. Построим подробную векторную диаграмму этой цепи. Строим вектор напряжений и токи 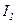 и
и 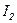 .
.
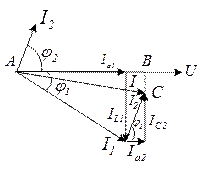
Разложим ток 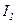 на две составляющие: активную
на две составляющие: активную 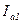 , которая совпадает по фазе с напряжением и индуктивную
, которая совпадает по фазе с напряжением и индуктивную 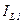 , которая отстающее по фазе от напряжения на угол
, которая отстающее по фазе от напряжения на угол 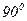 .
.
Эти составляющие определяем по формулам прямоугольного треугольника. 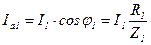 ,
, 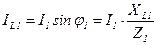 , где
, где 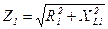 ;
; 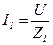
Разложим ток 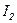 на две составляющие: активную
на две составляющие: активную 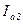 , которая совпадает по фазе с напряжением и индуктивную
, которая совпадает по фазе с напряжением и индуктивную 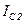 , которая опережает по фазе от напряжения на угол
, которая опережает по фазе от напряжения на угол 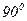 .
.
Эти составляющие определяем по формулам прямоугольного треугольника 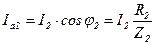 ,
, 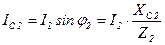 , где
, где 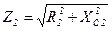 ;
; 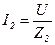
Складываем токи 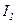 и
и 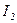 на векторной диаграмме и получаем общий ток
на векторной диаграмме и получаем общий ток 
Из треугольника АВС следует