Расчет однорядной пружины

Статическая нагрузка на одну пружину определяется по формуле (5.1):

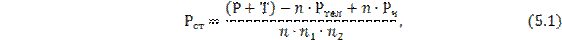
где Р – грузоподъемность 68,6 т;

Т – тара вагона 24,7 т;

Р_тел – вес тележки, 4,78 тс (478 кН);

Р_ч – вес частей тележки, находящимися над пружинами, 0,443 тс(4,43 кН);

n, n₁, n₂ – число тележек под вагоном, число рессорных комплектов в тележке и число пружин в комплекте соответственно.

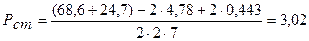тс.

Эквивалентная жесткость пружины определяется по формуле (5.2):

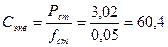тс/м (5.2)

где f_ст – прогиб рессорного подвешивания, 0,05 м.

Максимальная нагрузка, воспринимаемая пружиной вычисляется по формуле (5.3):

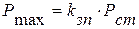, (5.3)

где k_зп – коэффициент запаса прогиба, 1,8 – 2,0.

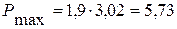(тс)

Максимальный прогиб пружины, соответствующий максимальной нагрузке определяются по формуле (5.4):

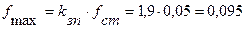(м) (5.4)

Диаметр прутка пружины вычисляется по формуле (5.5):

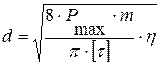, (5.5)

где 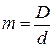– индекс пружины. Для расчета принимаем .

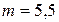D – средний диаметр пружины.

d – диаметр прутка пружины.

h – коэффициент, учитывающий кривизну витков пружины :

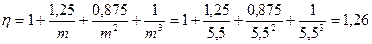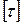– допускаемое касательное напряжение, .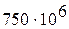

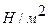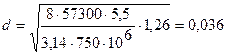(м)=36 (мм)

Средний диаметр пружины вычисляется по формуле (5.6):

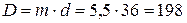(мм) (5.6)

Число рабочих витков вычисляется по формуле (5.7):

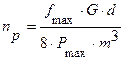, (5.7)

где G – модуль упругости второго рода, .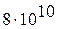

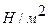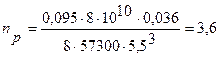
Высота пружины в сжатом состоянии определяется по формуле (5.8):

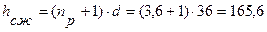(мм) (5.8)

Высота пружины в свободном состоянии определяется по формуле (5.9):

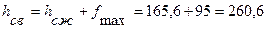(мм) (5.9)

Сравнивая параметры пружины: средний диаметр, диаметр прутка и высоту в свободном состоянии с возможными размерами пружин рессорного комплекта (170 мм, 30 мм и 249 мм) видим, что данная пружина не подходит. Поэтому однорядную пружину заменим двухрядной.

5.2 Расчет двухрядной пружины

Однорядную эквивалентную пружину заменяем на двухрядную из следующего условия (рисунок 6).

Для :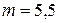

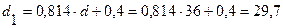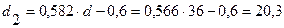(мм) (мм)

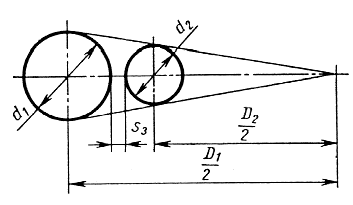
Рисунок 7 – Соотношение размеров двухрядной пружины

Диаметры прутков округляем до ближайших значений по ГОСТ 7417-75 «Сталь калиброванная. Сортамент». Принимаем d1 =30мм ,d2 =20,5мм.

Определяем распределение нагрузки между пружинами по формуле (5.10):

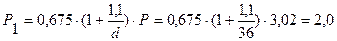(кН) (5.10)

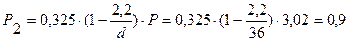(кН)

Определяем жесткость пружин по формуле (5.11):

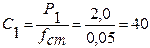(тс/м) (5.11)

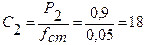(тс/м)

Суммарная жесткость двух параллельно стоящих пружин определяется по формуле (5.12):

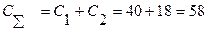(тс/м) (5.12)

Ошибка вычислений:

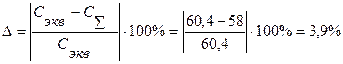
Средние диаметры пружин определяем по формуле (5.13):

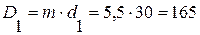(мм) (5.13)

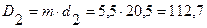(мм)

Число рабочих витков определяем по формуле (5.14):

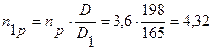(5.14)

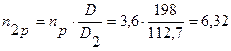
Высота пружин в сжатом состоянии определяем по формуле (5.15):

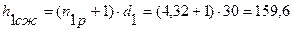(мм) (5.15)

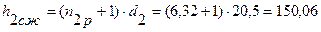(мм)

Выравнивание высот пружин производим путем увеличения числа рабочих витков из условия:

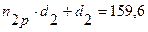(мм);

.

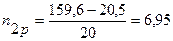Тогда = .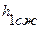

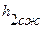Высота пружин в свободном состоянии определяем по формуле (5.16):

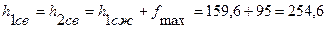(мм) (5.16)

Полное число витков определяем по формуле (5.17):

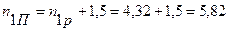(5.17)

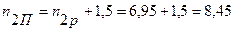
Длина заготовок определяем по формуле (5.18):

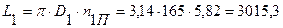(мм) (5.18)

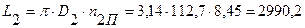(мм)

Опорные поверхности пружин выполняются плоскими и перпендикулярными оси пружины. Для этого концы заготовки пружины оттягиваются на длине не менее 2/3 длины витка.

Высота оттянутого конца пружины должна быть не более 1/3 диаметра прутка, а ширина – не менее .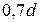

Геометрические размеры пружины изображены на рисунке 8.

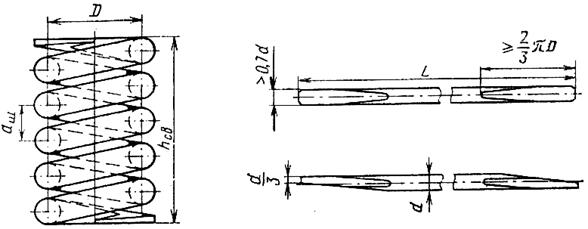
Рисунок 8 – Геометрические размеры пружины