Решение задач массового обслуживания

Системы массового обслуживания с отказами

Граф состояний многоканальной системы массового обслуживания с отказами имеет вид:

Здесь λ – интенсивность входящего потока требований, n - производительность одного канала (прибора) обслуживания,

S₀, S₁, S_k, S_n – состояния системы (индекс указывает число требований в системе), n - общее число каналов.

Вероятности состояний определяются по формуле

,

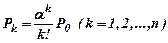где a=λ/n, а вероятность Р₀ находится из выражения

.

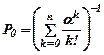Задача. В мастерскую по ремонту ЭВМ, где работают три мастера-ремонтника, поступают заказы от владельцев ЭВМ на проведение ремонта. Если работой заняты все три мастера, то вновь поступающий заказ не принимается, и владелец ЭВМ вынужден обратиться в другую ремонтную организацию. Пусть среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок – одно требование за 4 часа (0,25 треб/ч). Найти вероятность отказа и среднее число

занятых мастеров.

Имеем: n = 3, λ = 0,25(треб/ч), `Т_обс = 3ч. Находим:

a = λ/n = λ ×`Т_обс = 0,25 × 3 = 0,75,

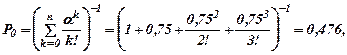
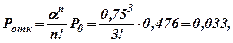
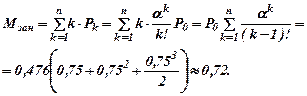
Таким образом, Р_отк = 0,033; М_занят = 0,72 мастера.

Системы массового обслуживания

с ограниченной длиной очереди

Граф состояний многоканальной системы массового обслуживания, имеющей n каналов, с ограниченной очередью, число мест в которой ограничено величиной l имеет вид:

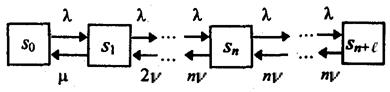
Вероятности состояний S₁, S₂, …, S_n находят по формуле

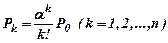
Вероятности состояний S_n+1, S_n+2, …, S_n+l находят по формуле

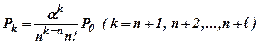
Вероятность Р₀ рассчитывается по формуле

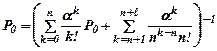
В большинстве практических задач отношение a/n<1. Формула для Р₀ используется в виде

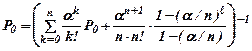
Задача. На автозаправочной станции установлены три колонки для выдачи бензина. Около станции находится площадка на три машины для ожидания в очереди. На станцию прибывает в среднем две машины в минуту. Среднее время заправки одной машины 1 мин. Требуется определить вероятность отказа и среднюю длину очереди.

Имеем: n=3, l=3, λ=2 (1/мин),`Т_обс=1 (мин),

n=1/`Т_обс=1 (1/мин). Находим: a=λ/n = 2/1=2, a/n=2/3.

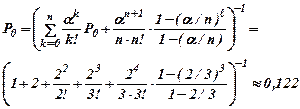
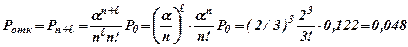
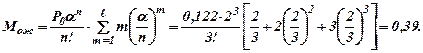
Таким образом, Р_отк=0,048, М_ож=0,39 (машины).

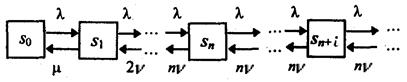
Системы массового обслуживания с ожиданием

Граф состояний системы массового обслуживания с ожиданием аналогичен графу состояний системы с ограниченной длиной очереди при условии, что граница очереди отодвигается в бесконечность:

Вероятности состояний находят по формулам

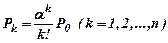
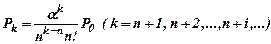
a/n<1 для определения Р₀ используют формулу

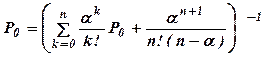
Задача. Фирма имеет две площадки для разгрузки грузового транспорта. Интенсивность потока грузов равна 0,8 (машины в час). Среднее время разгрузки одной машины составляет 2 часа. Предполагается, что очередь ожидающих разгрузки машин может быть неограниченной длины.

Найти среднее число занятых площадок и среднее время пребывания машины в ожидании.

Имеем: n=2, λ=0,8 (1/час), n = 1 /`Тобс=0,5 (1/сут),

a=λ/n = 0,8/0,5 = 1,6. Находим:

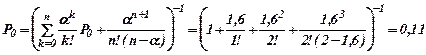
Среднее число занятых обслуживанием приборов n_з. Относительная пропускная способность q.

n_з =aq; q=1-P_отк= 1; n_з = 1,6

Среднее количество требований, ожидающих обслуживания

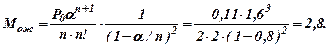
Среднее время ожидания

`Т_ож= М_ож/λ =3,5 час

Итак, n_з = 1,6 (площадки), `Т_ож =3,5 (сут).

Системы массового обслуживания

с ограниченным временем ожидания

В системах массового обслуживания с ограниченным временем ожидания время ожидания в очереди каждого требования ограничено случайной величиной t_ож, среднее значение которой`t_ож. Граф состояний такой системы:

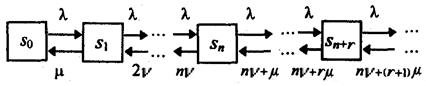
Величина, обратная среднему времени ожидания, означает среднее количество требований, покидающих очередь в единицу времени: μ=1/`t_ож.

При наличии в очереди r требований интенсивность потока покидающих очередь требований составляет rμ.

Формулы для определения вероятностей состояний такой системы имеют вид

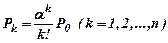
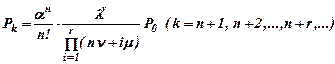
Вероятность Р₀ определяют по формуле

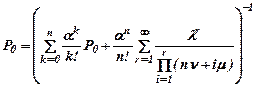
В практических задачах сумму бесконечного ряда вычислить достаточно просто, так как члены ряда быстро убывают с увеличением номера.

Задача. В фирме имеется три аппарата для чистки. Интенсивность потока посетителей λ=6 (посетителей в час). Интенсивность обслуживания посетителей одним аппаратом n = 3 (посетителей в час). Среднее количество посетителей, покидающих очередь, не дождавшись обслуживания, μ =1 (посетитель в час). Найти абсолютную пропускную способность фирмы.

Имеем: n=3, λ =6, n=3, μ =1. Находим: a=λ/n = 6/3=2,

.

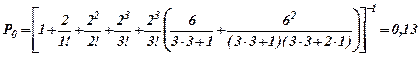Вероятность занятости всех приборов равна Р_зан=1-Р₀=0,87. Тогда абсолютная пропускная способность может быть получена как произведение: А=n×Р_зан=3×0,87=2,61. Таким образом, А =2,61 (посетителя в час).

Замкнутые системы массового обслуживания

В замкнутых системах массового обслуживания источник требований находится внутри системы, и интенсивность потока требований зависит от состояния самой системы. Чаще всего потоком требований в такой системе является поток неисправностей от некоторой группы работающих устройств. Пусть имеется m работающих устройств, которые могут выходить из строя за счет неисправностей. Имеется также n приборов (каналов) обслуживания этих требований. В качестве таких каналов могут выступать и люди. Обычно предполагают, что n<m.

Обозначим через S₀ состояние, при котором все устройства работают, а приборы обслуживания не заняты; S₁ - состояние, при котором одно устройствё вышло из строя и обслуживается одним прибором обслуживания; S_n - n устройств не работают и все приборы заняты обслуживанием; S_m - все устройства не работают, из них n обслуживаются и m-n ждут обслуживания. Граф состояний такой системы:

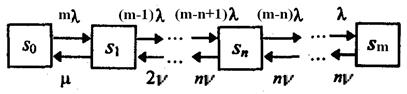
Вероятности состояний замкнутой системы определяются следующими зависимостями:

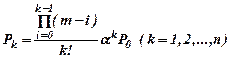
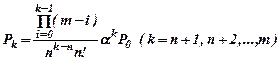
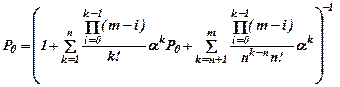
Задача. Рабочий обслуживает группу, из трех станков. Каждый станок останавливается в среднем два раза в час. Процесс наладки занимает в среднем 10 мин. Определить абсолютную пропускную способность наладки рабочим станков.

Имеем: n = 1, m = 3, λ=2, `Т_обс= 1/6, n = 6.

Находим: a=λ/n= 1/3

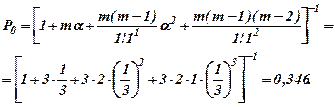
Определяем вероятность того, что рабочий будет занят обслуживанием: Р_зан=1-Р₀=1-0,346=0,654.

Если рабочий занят обслуживанием, то он может обслужить 6 станков в час. Следовательно, абсолютная способность находится как произведение: А=nР_зан=6×0,654≈4.

Таким образом, А=4 (станка в час).

МНОГОМЕРНЫЙ АНАЛИЗ.