Методические принципы измерения кусковатости горной массы
Методы измерения кусковатости горной массы детально исследованы в монографии Л.И.Барона, где предлагалась следующая классификация таких методов:
1)прямые методы - измерения объема или массы предварительно выделенных фракций или единичных кусков, измерения по поверхности на фотографиях (фотопланиметрия) и в натуре;
2)косвенные методы - производственный учет расхода взрывчатых материалов (капсюлей детонаторов, ВВ и шпурометров) при вторичном дроблении; экспериментальное определение зависящих
от кусковатости горной массы параметров производительности и энергоемкости работы погрузочных, транспортных и других обрабатывающих машин и механизмов.
Многолетний практический опыт определения гранулометрического состава дробленых горних пород позволил выработать определенные правила отбора и анализа проб. Цель этих правил состояла в прямых методах определения содержания по массе различных фракций исследуемого материала и в обосновании ряда интервалов размеров кусков дробленого материала, составляющих эти фракции. Причем ряд анализируемых фракций (интервалов > размеров) должен был соответствовать законам распределения исследуемых совокупностей.
Мультипликативный характер формирования совокупности кусков горной массы при каждом шаге дробления вызывает пропорциональное изменение размеров исходных кусков, поэтому в качестве наиболее простой последовательности интервалов размеров выбрана была геометрическая прогрессия. Соответствующий интервальный ряд использовался длительное время для ситового анализа различных по размерам, физико-механическим свойствам и способам получения продуктов дробления. Для удобства сравнения результатов гранулометрического анализа был принят единый знаменатель геометрической прогрессии, равный Ö2.
Ряд средних размеров интервалов в этой последовательности строится по формуле бесконечной геометрической прогрессии 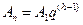 , где А1 - первый член геометрической прогрессии, соответствующий максимальному размеру молекулы кристаллического вещества, для удобства анализа
, где А1 - первый член геометрической прогрессии, соответствующий максимальному размеру молекулы кристаллического вещества, для удобства анализа 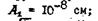 q- знаменатель
q- знаменатель
геометрической прогрессии, 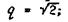 п- номер интервального ряда.
п- номер интервального ряда.
Нижняя и верхняя границы интервалов размеров (табл.3) в такой последовательности соответственно 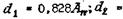
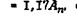 средний арифметический размер фракции
средний арифметический размер фракции
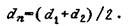 (35)
(35)
В табл.3 представлена часть бесконечной геометрической последовательности интервалов, диапазон размеров которой полностью удовлетворяет требованиям гранулометрического, анализа, устанавливающего соотношение масс кусков. Размер кусков горной массы в этой последовательности меняется от десятков микрон (предельный размер, поддающийся разделению на встряхиваемых в воздухе ситах) до нескольких метров - максимального размера негабаритных кусков горной массы. Размер интервала, равный размеру земного шара в этой-системе, соответствует номеру интервала 115.
Таблица 3
Размеры геометрической последовательности интервалов размеров при гранулометрическом анализе дробленого материала
| Номер | Размеры интервальной сетки, см | Номер | Размеры интервальной | ||
| интервала. | интервала | сетки. | см | ||
| крайние | средний | крайние | средний | ||
| 0,00517 | 1,33 | ||||
| 0,00732 | 0,00625 | 1,87 | 1,60 | ||
| 0,01035 | 0,00883 | 2,65 | 2,28 | ||
| 0,01445 | 0,0125 | 3,75 | 3,20 | ||
| 0,0178 | 4,61 | ||||
| 0,02071 | 0,0250 | 5,41 | 8,76 | ||
| 0,02929 | 7,81 | ||||
| 0,0353 | 9,63 | ||||
| 0,04142 | 11,3 , | ||||
| 0,05857 | 0,0500 | 18,3 | 13,9 | ||
| 0,08284 | 0,707 | 23,5 | 20,1 | ||
| 0,1171 | 0,1000 | 33,2 | 29,0 | ||
| 0,1657 . | 0,1414 | 47,9 | 41,8 | ||
| 0,2343 | 0,2000 | 89,2 | 60,4 | ||
| 0,3313 | 0,2830 | 99,9 | 87,3 | ||
| 0,4886 | 0,4000 | 144,2 | 125,9 | ||
| 0,6627 | 0,5656 | 203,4 | 181,8 | ||
| 0,9373 | 0,8000 | 293,7 | 282,2 | ||
| 1,33 | 1,1314 | 424,0 | 387,9 |
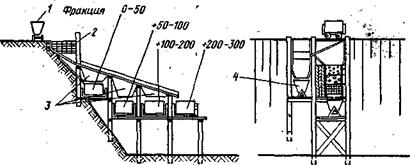
Реальные гранулометрические составы горной массы будут распределены в этой последовательности очень неравномерно, и для их анализа необходимо выбирать каждый раз некоторую последовательность шести-десяти сит. Методы гранулометрического анализа продуктов дробления в обогащении используют эту последовательность сит и проводят анализ на приборе, принципиальная схема которого предусматривает грохочение материала в наборе сит с последующим взвешиванием каждой фракции (рис.б). Этот принцип легко осуществить для относительно малых размеров ячейки (в несколько сантиметров). Проводить анализ материала, содержащего более крупные куски, таким способом затруднительно, поскольку система грохотов для расситовки кусков массой
 |
 |
Рис, 6. Установка для ситового
анализа горной массы 1 - вагонетка с рудой; 2 - решетка грохота; 3 - лотки грохотов; 4 - вагонетка для сбора подситового продукта
в несколько килограммов и больше представляет собой сооружение с весьма сложной и энергоемкой системой привода, загрузки, выгрузки и анализа. Поэтому распределение масс проектов взрывного дробления не может быть определено, и существующими методами анализируется лишь часть общей совокупности.
Рассматривая проблему анализа какой-либо части исходной совокупности кусков, сталкиваемся прежде всего с принципиальным вопросом обоснования объема необходимой выборки и правил отбора той части совокупности, по которой проводится анализ. Так для конкретного гранулометрического анализа формулируется общая статистическая задача выборочного анализа из практически бесконечной статистической совокупности элементов.
Выбор последовательности интервалов анализа этой проблемы не затрагивали, молчаливо предполагая, что существующая статистическая теория «малой выборки» полностью подходит к данному случаю. Какие же действительные предпосылки позволяли принимать статистическую гипотезу малой выборки?
Любой вид статистического контроля производственного материала имеет настолько большой объем генеральной совокупности, т.е. исходного дробленого материала, вырабатываемого данной технологией, что анализ всего этого объема практически невозможен, так как для него необходимо вводить специальную технологию расситовки (грохочения) и последующего взвешивания в рамках поточной технологии дробильных фабрик или мельничных корпусов, что потребовало бы чрезвычайно больших затрат. Причем расситованный продукт, по-видимому, не всегда удовлетворял бы потребностям данной технологии, заставляя прибегать к усредняющему смешиванию расситованного материала.
Любая часть исходного материала, взятая для гранулометрического анализа, должна содержать "достаточно большое число частиц. На каждом сите (в каждом интервале размеров) должно находиться заметное количество кусков, удовлетворяющее требованиям малой выборки при случайном способе отбора всей пробы. Это требование выполняется при ситовом анализе, поскольку крупность дробленого материала невелика, а крупные частицы можно объединять в открытые интервалы крупности больше хтах (здесь xmах- крупность ячейки верхнего сита, относительно которого отбирается нужное, количество кусков).
Итак, обычный гранулометрический состав дробленого материала будет распределен примерно по десяти интервалам стандартного интервального ряда при условии объединения малых количеств материала в открытые интервалы меньше хтin и больше хтах.
Выбор необходимого количества анализируемых интервалов должен обеспечивать однозначное определение всех параметров исследуемой статистической совокупности, т.е. количество степеней свободы при сравнении теоретической статистической модели с реальными параметрами распределения должно быть больше нуля.
При оценке соответствия экспериментальных данных той или иной теоретической модели известным в статистике критерием Пирсона ,g 2 число степеней свободы
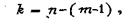
где п - число интервалов анализа; т - число параметров закона распределения, которые необходимо определить.
Таким образом, даже в случае максимального простого приближения к статистическому закону распределения с двумя независимыми параметрами k = п - 3. В случае дополнительного ограничения, связанного с усечением., первоначального закона распределения,, к =n-4. Следовательно, даже при оценке наиболее простых законов распределения минимальное число интервалов должно быть не менее пяти, а при открытых границах крайних интервалов - не менее шести. Это относится к любым способам прямого определения гранулометрического состава горной массы. При этом желательно иметь представительные количества исследуемого материала в крайних интервалах. При шести исследуемых интервалах количество материала в крайних должно составлять около 17%., а при известной, четко установленной границе верхнего интервала и при пяти исследуемых интервалах - около 20 %.
Уже отмечалось, что такие простые статистические схемы не всегда оправданы для аппроксимации реальных законов распределения дробленого материала. Возможны случаи бимодальных или многомодальных распределений. Предполагая, что каждой моде соответствует два независимых параметра закона распределения, а общая совокупность представляет собой сумму двух или нескольких независимых законов распределения, число исследуемых интервалов можно определить по формуле
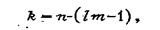 (36)
(36)
где l - число исследуемых законов распределения.
При двухмодальном, усеченном по максимальному размеру куска законе распределения и открытых границах крайних интервалов число исследуемых интервалов должно быть больше семи. В случае более сложных аппроксимаций необходимо увеличить число исследуемых интервалов до 10-12, тогда количество материала в последнем интервале должно составлять 8-10 % от выборки. .
Еще одним важным вопросом гранулометрического анализа является вопрос об оптимальной выборке, т.е. об определении минимального количества горной массы, необходимого для получения теоретических характеристик закона распределения заданной точности. Следует отметить, что объем выборки зависит от размера куска горной массы при любом способе оценки гранулометрического состава, будь то линейное опробование, фотопланиметрия или весовой метод. Объем выборки по каждому из этих способов в той или иной мере зависит от крупности анализируемого материала. Единственным не зависимым от размера способом гранулометрического анализа является количественное опробование, которое устанавливает долю количества частиц, имеющих определенные размеры.
На основании логарифмически-нормальной аппроксимации данных гранулометрического анализа всегда можно определить аналитические соотношения между различными характеристиками совокупности (поверхностной, линейной, количественной, по массе).
Основное свойство логарифмически-нормального закона распределения формулируется следующим образом: если величина x имеет логарифмически-нормальное распределение с параметрами х и β, то любая степенная функция z =С xg (здесь С - постоянная; g- показатель степени) также будет распределена логарифмически-нормально с той же величиной логарифмической дисперсии. Это свойство иллюстрируется следующими преобразованиями:
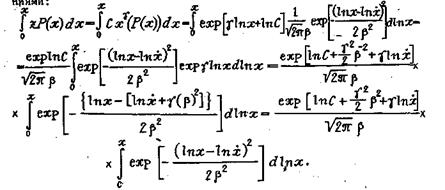 |
Иначе говоря, пропорциональное изменение случайной величины меняет среднее геометрическое значение ее, а дисперсия остается постоянной.
Воспользовавшись этим свойством логарифмически-нормального закона распределения, можно определить соотношения между средними геометрическими размерами кусков горной массы при различных способах гранулометрического анализа. Если функция распределения Ф(х) определяет долю количества кусков размера меньше X , то доля линейного размера кусков размера меньше х’
 |
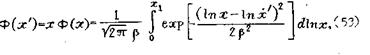
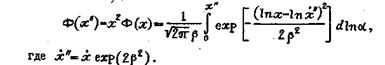 |
Доля поверхности кусков размера меньше х
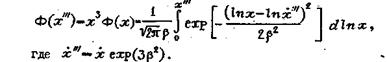 |
Доля объема (или массы) кусков размером меньше x
Подобные преобразования характеризуют полное логарифмически-нормальное распределение любого из показателей гранулометрического состава. В вероятностно-логарифмической сетке соответствующий пересчет будет соответствовать параллельному переносу кривой распределения на расстояния соответственно еb2, е2b2 и е3b2 (рис.7).
Уже говорилось (гл.1), что практически повсеместно для аппроксимации опытных данных необходимо использовать усеченный логарифмически-нормальный закон распределения. В этом случае, ,даже если доля количества частиц, имеющих размер больше х-тах невелика, т.е. поправка на усечение у; этого распределения незначительна, то после пересчета по формуле (32) может оказаться, что доля массового определения данных гранулометрического состава весьма заметна. Тогда необходимо вводить в формулы (53)-(55) поправку на усечение по зависимостям (33) и (34).
Ошибка в определении -среднего геометрического или среднего арифметического логарифмов размеров
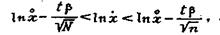
где х0 и х.. - среднее геометрическое соответственно генеральной и выборочной совокупности; t - число Стьюдента; β - логарифмическая дисперсия (нормированное отклонение); N - количество кусков в пробе.
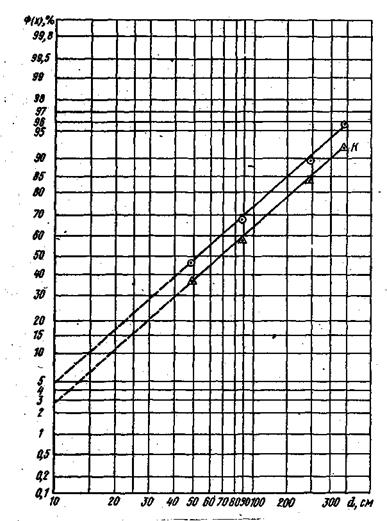 |
Рис.7. Гранулометрический состав горной массы 1 - распределение по массе; 2 - планиметрический способ; К- точка усечения
После преобразований получим
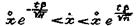
Абсолютная ошибка определения среднего геометрического размера кусков для половины распределения (правой относительно среднего размера частиц) 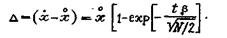
Следовательно, относительная ошибка среднего (в процентах)
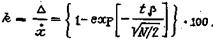
При малых значениях относительной ошибки среднего (примерно 10-15 %) величина 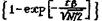 будет мало отличаться от tb/ÖN/2 , тогда относительная ошибка среднего геометрического размера кусков горной массы (в процентах)
будет мало отличаться от tb/ÖN/2 , тогда относительная ошибка среднего геометрического размера кусков горной массы (в процентах)
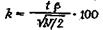 |
(37)
а соответствующий этой ошибке объем выборки
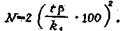 |
(38)
Для обеспечения точности среднего, равной 10 %, при надежности 0,9 (что соответствует коэффициенту Стьюдента t = 1,65) необходимо около 1500 подсчитанных кусков, тогда логарифмическая дисперсия будет близка к единице. Следует помнить, что увеличение логарифмической дисперсии увеличивает объем выборки по квадратичному закону.
Оценка центра логарифмически-нормального распределения средним геометрическим размером кусков дает приемлемую точность в определении среднего лишь при малых значениях логарифмической дисперсии; Увеличение степени рассеяния вокруг среднего значения приводит к уменьшению эффективности среднего арифметического как характеристики математического ожидания распределения.
Абсолютная ошибка определения среднего арифметического
по данным выборочного анализа
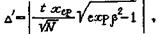
а относительная ошибка среднего арифметического (в процентах)
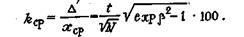 |
(39)
Соответствующий объем выборки
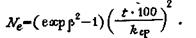 |
(40)
Для определения среднего арифметического с той же точностью, что и среднего геометрического, необходимо примерно в два раза больше кусков.
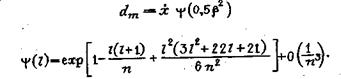 |
Более точная оценка центра распределения может быть получена с помощью максимальных правдоподобных оценок. Максимально правдоподобная оценка математического ожидания y определяется в виде
или
Абсолютная ошибка максимально правдоподобной оценки математического ожидания
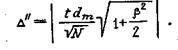
Относительная ошибка максимально правдоподобной оценки (в процентах)
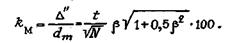 (41)
(41)
Поскольку всегда b>0, точность определения максимально правдоподобной оценки математического ожидания при равной выборке всегда выше точности определения среднего арифметически го( 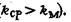
Сопоставление зависимостей (40) и (41) показывает, что ошибка определения среднего геометрического размера куска совпадает с ошибкой определения максимально правдоподобной оценки при значениях логарифмической дисперсии, мало отличающихся от единицы.
Необходимый объем выборки при других методах гранулометрического анализа (линейном, поверхностном или по массе) определяется умножением необходимого при заданной точности количества кусков горной массы на соответствующую степень математического ожидания этого распределения.
Необходимая поверхность при фотопланиметрии
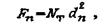
где-NT - объем выборки количества частиц; dn- математическое ожидание поверхности кусков при фотопланиметрическом анализе.
Необходимая выборка исследуемой совокупности по массе
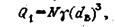
где dв - математическое ожидание размера куска.
Горную массу со средним размером куска около 150 мм и логарифмической дисперсией равной единице, можно проанализировать с точностью определения среднего геометрического, математического ожидания и дисперсии около 10 % при объеме выборки примерно 1500 кусков, поверхности развала около 300 м2 и массе около 200 т.

 Таким образом, простейший анализ основных принципов отбора и обработки данных гранулометрического анализа определил довольно жесткие требования к методике отбора проб, которые сводятся к следующим положениям:
Таким образом, простейший анализ основных принципов отбора и обработки данных гранулометрического анализа определил довольно жесткие требования к методике отбора проб, которые сводятся к следующим положениям:
1.При любом способе гранулометрического анализа необходимо получить геометрическую последовательность, интервалов размеров кусков.
2.Количество исследуемых интервалов для реальной совокупности кусков горной массы должно составлять шесть-десять интервалов, чтобы статистические характеристики аппроксимирующего закона распределения можно было определить с приемлемой точностью.
3.Объем выборки существенно зависит от крупности анализируемого материала и величины разброса размеров кусков (логарифмической дисперсии). Причем предварительная оценка наиболее типичных распределений характеризует примерный объем выборки в 100-200 т материала.
Необходимым условием реализации всех перечисленных принципов отбора и анализа данных гранулометрического анализа является хорошее усреднение размеров кусков в генеральной совокупности.
Крайне неравномерное распределение размеров кусков в развале, полученном при взрывных работах, ставит вопрос о такой организации анализа, при которой необходимый объем выборки равномерно распределяется по всему объему отбитой горной массы.
