Метод решения несобственного интеграла с бесконечным нижним пределом

Данный раздел предназначен для тех, кто хорошо разобрался с уроком Несобственные интегралы. Примеры решения, или, по крайне мере, понял бОльшую его часть.

Речь пойдет о несобственных интегралах первого рода с бесконечным нижним пределом:

.

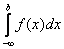Пример 7

Вычислить несобственный интеграл или установить его расходимость

.

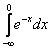Чем отличается данный интеграл от «обычного» несобственного интеграла с бесконечным верхним пределом? По технике решения практически ничем. Так же нужно найти первообразную (неопределенный интеграл), так же нужно использовать предел при вычислении интеграла. Отличие состоит в том, что необходимо устремить нижний предел интегрирования к «минус бесконечности»:

.

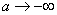Из вышесказанного следует очевидная формула для вычисления такого несобственного интеграла:

.

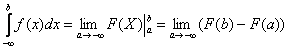В данном примере, подынтегральная функция непрерывна на 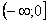и:

,

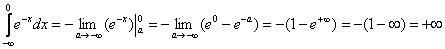то есть, несобственный интеграл расходится.

Вот тут, главное, быть аккуратным в знаках и не забывать, что 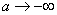. Нужно внимательно разобраться, что куда стремится.

Пример 8

Вычислить несобственный интеграл или установить его расходимость

.

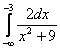Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Метод решения несобственного интеграла с бесконечными пределами интегрирования

Очень интересный случай. Несобственный интеграл первого рода с двумя бесконечными пределами интегрирования имеет следующий вид:

.

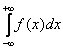Как его решать? Его нужно представить в виде суммы двух несобственных интегралов:

.

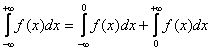Примечание: вместо ноля может быть любое число, но ноль обычно удобнее всего.

Если обаинтеграла правой части сходятся, то сходится и сам интеграл

Если хотя бы один из интегралов правой части расходится, то расходится и интеграл

.

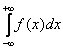Пример 9

Вычислить несобственный интеграл или установить его расходимость.

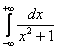
Мы специально подобрали простой пример, чтобы проиллюстрировать другой важный момент применения метода.

Подынтегральная функция непрерывна на всей числовой прямой.

Согласно правилу, интеграл следует представить в виде суммы интегралов:

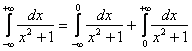
Интеграл будет сходиться, если будут сходиться оба интеграла правой части. Проверяем:

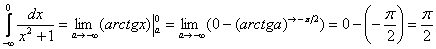
– сходится.

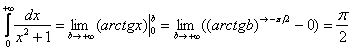
– сходится.

Оба интеграла сходятся, значит, сходится и весь интеграл:

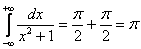
Теперь обратим внимание на подынтегральную функцию. Она является чётной.

В несобственных интегралах с (двумя) бесконечными пределами, а, значит, симметричными интервалами интегрирования, чётностью пользоваться МОЖНО.Аналогично определенному интегралу, интервал интегрирования можно разделить, а результат – удвоить. То есть, решение допустимо записать короче:

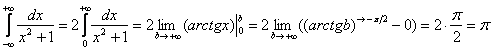
Почему такое возможно?

График подынтегральной чётной функции симметричен относительно оси OY. Следовательно, если половина площади конечна (интеграл сходится) – то симметричная половина площади тоже конечна.

Если же половина площади бесконечна (интеграл расходится), следовательно, симметричная половина тоже будет расходиться.

Пример 10

Вычислить несобственный интеграл или установить его расходимость.

.

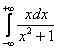Подынтегральная функция непрерывна на всей числовой прямой. Согласно правилу, интеграл нужно представить в виде суммы двух интегралов:

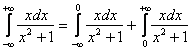
Проверяем сходимость интегралов правой части:

.

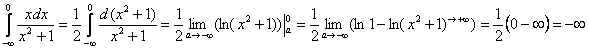Первый интеграл расходится. Знак «минус» говорит о том, что бесконечная криволинейная трапеция расположена ниже оси абсцисс.

Не нужно проверять сходимость второго интеграла правой части, поскольку для того, чтобы интеграл

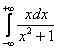
сходился, необходимо чтобы сходились обаинтеграла правой части.

Ответ:несобственный интеграл

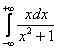
расходится.

А сейчас очень важный момент: подынтегральная функция

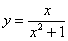
является нечётной.

В несобственных интегралах с бесконечными пределами (т. е. симметричными интервалами интегрирования) нечётностью пользоваться НЕ СЛЕДУЕТ!!!

В этом состоит отличие от определенного интеграла. Там всегда можно смело записать:

,

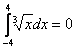а здесь так поступать – не следует. Почему? Потому что в ряде случаев, как, например, в рассмотренном примере, получится нонсенс (бессмыслица). Если считать, что

,

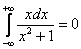то интеграл будет сходящимся (поскольку получено конечное число), но в то же время его часть:

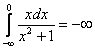
– расходится (как мы только что показали в решении). Тонкость же состоит в том, что несобственный интеграл равен своему значению только в предельном смысле. Интеграл

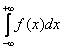
от нечетной функции f(x), в принципе, может стремиться (а не равняться) к нулю, но нельзя сразу записывать, что

.

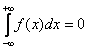Всегда представляем интеграл в виде двух интегралови выполняем проверку на сходимость по стандартному алгоритму.

Пример 11

Вычислить несобственный интеграл или установить его расходимость

.

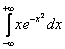Полное решение и ответ в конце урока.