Метод аналитического выравнивания
Метод постоянной средней
| Квартал | Первый год | Второй год | Третий год | yi=(y1+y2+y3)/3 | Индекс сезонности = yi/ 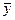 |
| I | 159,67 | 159,67/175 = 0,91 | |||
| II | 196/175 = 1,12 | ||||
| III | 180,67 | 180,67/175 = 1,03 | |||
| IV | 163,67 | 163,67/175 = 0,94 | |||
| Итого | |||||
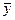 = 700/4 = 175 = 700/4 = 175 |
Метод аналитического выравнивания
| t | y | t2 | t*y | yt | y/yt | |
| -6 | -972 | 175+1,98*(-6)=163 | 0,99 | |||
| -5 | -850 | 1,03 | ||||
| -4 | -708 | 1,06 | ||||
| -3 | -453 | 0,89 | ||||
| -2 | -318 | 0,93 | ||||
| -1 | -193 | 1,12 | ||||
| 1,01 | ||||||
| 0,94 | ||||||
| 0,87 | ||||||
| 1,23 | ||||||
| 1,01 | ||||||
| 0,92 | ||||||
| Итого |
n =12 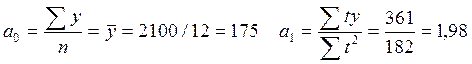
Уравнение тренда: yt = a0+a1*t = 175+1,98*t
| Квартал | Индекс сезонности |
| I | (0,99+0,93+0,87)/3 = 0,93 |
| II | (1,03+1,12+1,23)/3 = 1,13 |
| III | 1,03 |
| IV | 0,92 |
5. Имеются следующие данные о товарных запасах фирмы за второй квартал, тыс.руб.
| На 1/04 | На 1/05 | На 1/06 | На 1/07 | |
| Продовольственные товары | 4,8 | 4,0 | 5,0 | 5,2 |
Определите средние товарные запасы продовольственных товаров за второй квартал.
Решение:
Средние товарные запасы: 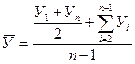 →
→ 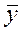 =
= 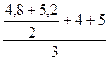 = 4,66
= 4,66
Тема 10. Индексный метод анализа.
1. Имеются следующие данные о проданных товарах:
| Товары | Единица измерения | Количество q, тыс.ед. | Цена p, руб. | ||
| Базисный период, q0 | Отчетный период, q1 | Базисный период, p0 | Отчетный период, p1 | ||
| А Б | кг л |
Определить:
1) индивидуальные индексы объемов продаж в натуральном выражении, цен и товарооборота;
2) агрегатные индексы физического объема по формулам Пааше и Ласпейреса;
3) агрегатные индексы цен по формулам Пааше и Ласпейреса;
4) общий индекс товарооборота;
5) абсолютные приросты товарооборота за счет изменения объемов продаж, цен и за счет совместного действия обоих факторов.
Решение:
| Товарооборот, тыс.руб | ||||
| Базисный период T0 = q0*p0 | Отчетный период T1 = q1*p1 | q1*p0 | q0*p1 | |
| А | ||||
| Б | ||||
| Итого | ||||
| А | Б | |||
| Индивидуальные индексы объемов = iq = q1/q0 | 0,75 | 0,9 | ||
| Индивидуальные индексы цен = ip = p1/p0 | 1,33 | 1,2 | ||
| Индивидуальные индексы товарооборота = iqp = T1/T0 | 1,08 | |||
Агрегатный индекс физ. объема : IqЛ = 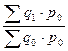 = 0,81 или 81% IqП = = 0,81 или 81% IqП = 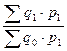 = 0,81 или 80,6% = 0,81 или 80,6% | ||||
Агрегатный индекс цен: IpЛ = 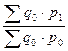 = 1,28 или 128% IpП = = 1,28 или 128% IpП = 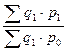 = 1,27 или 127,4% = 1,27 или 127,4% | ||||
Общий индекс товарооборота: Iqp= 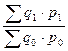 = 1,03 или 103,2% = 1,03 или 103,2% | ||||
| Абсол.прирост товарооборота за счет изменения объемов = Σq1 p0- Σq0 p0 = - 4750 тыс.руб. | ||||
| Абсол.прирост товарооборота за счет изменения цен = Σq1 p1- Σq1 p0 = 5550тыс.руб. | ||||
| Абсол.прирост товарооборота = ΣT1-ΣT0 = 800тыс.руб. |
2. Имеются следующие производственные показатели по предприятию:
| Вид продукции | Изменение объема выпуска продукции в III квартале по сравнению с II кварталом, % | Общие затраты рабочего времени на производство продукции в II квартале тыс.чел.-час. |
| КЛ-1 МН-6 | -6 +3 |
Определить на сколько процентов изменился выпуск продукции по двум видам.
Решение:
| (iq-1)*100% | T0=q0*t0 | iq=q1/q0 | iq*T0 =q1* t0 |
| -6 | 0,94 | 11,28 | |
| 1,03 | 8,24 | ||
| Итого | 19,52 |
Iq = 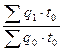 =
= 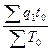 = 19,52/20 = 0,976 = 97,6% Изменение на 97,6-100 = -2,4%
= 19,52/20 = 0,976 = 97,6% Изменение на 97,6-100 = -2,4%
3. Имеются данные о вкладах населения в Сбербанке:
| Группа населения | Размер вклада, руб. | Удельный вес вкладов в общем их числе | ||
| Базисный период, Х0 | Отчетный период, Х1 | Базисный период, 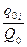 | Отчетный период, 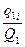 | |
| Городское Сельское | 0,5 0,5 | 0,6 0,4 |
Определить общие индексы среднего размера вклада переменного состава, постоянного состава, структурных сдвигов.
Решение:
| Х0 | Х1 | 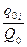 | 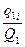 | 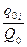 *Х0 *Х0 | 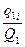 *Х1 *Х1 | Х0* 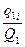 | |
| 0,5 | 0,6 | ||||||
| 0,5 | 0,4 | ||||||
| Итого |
Индекс переменного состава: 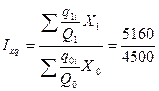 = 1,147 или 114,7%
= 1,147 или 114,7%
Индекс постоянного состава: 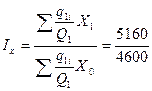 = 1,122 или 112,2%
= 1,122 или 112,2%
Индекс структурных сдвигов: 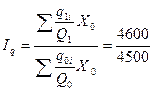 = = 1,022или 102,2%
= = 1,022или 102,2%
Проверка: Ixq = Ix * Iq = 1,147= 1,122*1,022
4. Имеются данные о выпуске однородной продукции по предприятиям АО:
| № пред- приятия АО | Выпуск продукции | Себестоимость единицы продукции, руб. | ||||
| I квартал | I I квартал | I квартал | II квартал | |||
| Тыс.ед. q0 | %, dq0 | Тыс.ед. q1 | %, dq1 | z0 | z1 | |
| 7,0 6,0 | 8,0 6,5 | |||||
| Итого | 6,4 | 6,95 |
Определить:
1) на сколько процентов в среднем изменился выпуск продукции в натуральном выражении;
2) индивидуальные индексы себестоимости продукции;
3) среднее изменение себестоимости продукции.
Решение:
| Себестоимость единицы продукции, руб. | Индивидуальный индекс себестоимости iz = z1 / z0 | Затраты З | |||
| I квартал z0 | II квартал z1 | I квартал З0 = q0z0 | II квартал З1 = q1z1 | q1z0 | |
| 1,143 | |||||
| 6,5 | 1,083 | ||||
| Итого |
В среднем выпуск продукции в натуральном выражении изменился:
Iq = 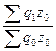 = 756/640 = 1,18 или увеличился на 18%
= 756/640 = 1,18 или увеличился на 18%
Среднее изменение себестоимости продукции: Iz = 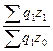 =
= 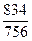 = 1,103 или увеличится на 10,3%
= 1,103 или увеличится на 10,3%
5. Имеются следующие данные о реализации фруктов на городском рынке:
| Продукт | Товарооборот в январе, тыс.руб. | Изменение цены в январе по сравнению с декабрем, % |
| А | +2,7 | |
| Б | +3,1 |
Определить:
1) на сколько процентов в среднем изменились цены на всю реализованную продукцию;
2) прирост выручки от реализации за счет изменения цен (перерасход покупателей, вызванный ростом цен).
Решение:
| Продукт | Т1 = p1*q1, тыс.руб. | (ip-1)*100, % | ip = p1/p0 | Т1 / ip |
| А | 2,7 | 1,027 | 204,48 | |
| Б | 3,1 | 1,031 | 127,06 | |
| Итого | 331,54 |
В среднем цены на всю реализованную продукцию изменились:
Ip (Пааше) = 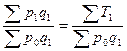 ;
; 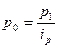 → Ip =
→ Ip = 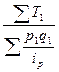 =
= 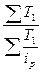 =341/331,54 = 1,0285
=341/331,54 = 1,0285
= 102,85 % или на 2,85%
Прирост выручки от реализации за счет изменения цен = ∑(р1-р0)*q1 = ∑T1- ∑ T1/ip = 9,46 тыс. руб.
