Требования к сдаче промежуточного контроля
Во время аудиторных занятий в период сессии студенты вместе с преподавателем изучают теорию курса. В период между сессиями студенты выполняют контрольную работу по пройденным темам и самостоятельно углубляются в теоретический материал.
Во втором семестре 1 курса проводится аттестация по предмету в форме ДИФФЕРЕНЦИРОВАННОГО ЗАЧЁТА. Допуском к аттестации является предоставление контрольной работы (в соответствии с вариантом).
Цель аттестации – определить наличие теоретических знаний и умение практического применения математических методов в профессиональной деятельности.
На зачете студент должен продемонстрировать:
знание
· основных понятий и определений по темам дисциплины «Элементы высшей математики»;
· основных расчетных формул.
умение
· работать с матрицами и определителями;
· решать системы линейных уравнений;
· решать задачи на действия с векторами;
· использовать при решении задач уравнения прямых и плоскостей;
· решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления;
· решать обыкновенные дифференциальные уравнения.
ПРИЛОЖЕНИЕ 1
Образец оформления титульного листа контрольной работы
Министерство общего и профессионального образования
Свердловской области
ГАПОУ СО «Областной техникум дизайна и сервиса»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ»
Исполнитель: ______________________
студент(ка) ФИО
г руппы__________ шифр___________
Проверил: Мерзляков А.В._
преподаватель ФИО
оценка __________________________
Екатеринбург, 20___
ПРИЛОЖЕНИЕ 2
ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
ТЕМА: ЛИНЕЙНАЯ АЛГЕБРА
ЗАДАНИЕ № 1
ЗАДАНИЕ: Вычислить определитель.
1.1. 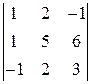 . 1.2.
. 1.2. 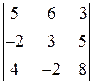 . 1.3.
. 1.3. 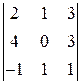 . 1.4.
. 1.4. 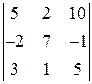 .
.
1.5. 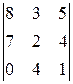 . 1.6.
. 1.6. 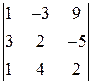 . 1.7.
. 1.7. 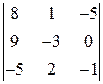 . 1.8.
. 1.8. 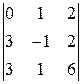 . 1.9.
. 1.9. 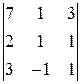 . 1.10.
. 1.10. 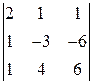 .
.
ЗАДАНИЕ № 2
ЗАДАНИЕ: Решить систему уравнений по правилу Крамера.
2.1. 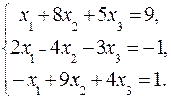 2.2.
2.2. 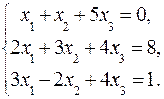
2.3. 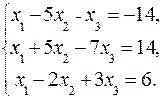 2.4.
2.4. 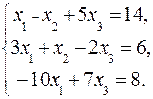
2.5. 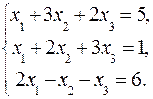 2.6.
2.6. 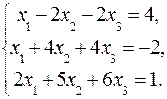
2.7. 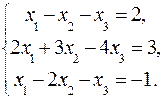 2.8.
2.8. 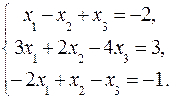
2.9. 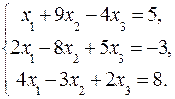 2.10.
2.10. 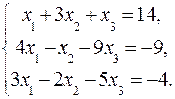
ЗАДАНИЕ № 3
ЗАДАНИЕ: Решить систему уравнений методом Гаусса.
3.1. 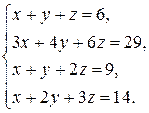 . 3.2.
. 3.2. 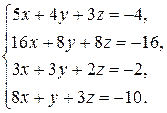 . 3.3.
. 3.3. 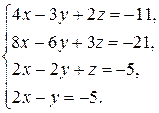 .
.
3.4. 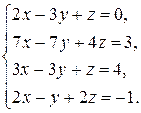 . 3.5.
. 3.5. 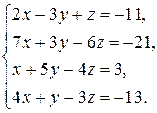 . 3.6.
. 3.6. 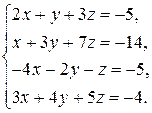 .
.
3.7. 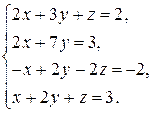 . 3.8.
. 3.8. 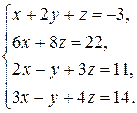 . 3.9.
. 3.9. 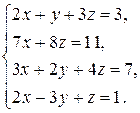 .
.
3.10. 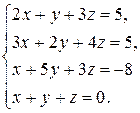 .
.
ТЕМА: ВЕКТОРНАЯ АЛГЕБРА
ЗАДАНИЕ № 4
ЗАДАНИЕ: Найти площадь и длины диагоналей параллелограмма, построенного на векторах 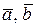 .
.
4.1. 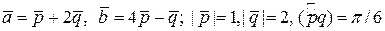 .
.
4.2. 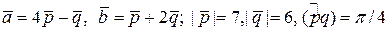 .
.
4.3. 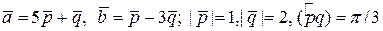 .
.
4.4.  .
.
4.5. 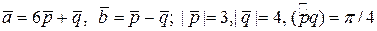 .
.
4.6. 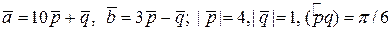 .
.
4.7. 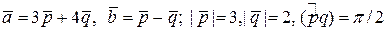 .
.
4.8. 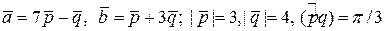 .
.
4.9. 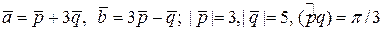 .
.
4.10. 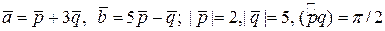 .
.
ЗАДАНИЕ № 5
5.1. Найти уравнение плоскости, проходящей через точки 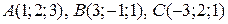 .
.
5.2. Найти уравнение плоскости, проходящей через точки 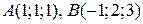 и параллельной оси ОХ.
и параллельной оси ОХ.
5.3. Найти уравнение плоскости, проходящей через точки 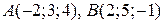 и параллельной оси ОУ.
и параллельной оси ОУ.
5.4. Найти уравнение плоскости, проходящей через точки 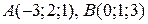 и параллельной оси ОZ.
и параллельной оси ОZ.
5.5. Найти уравнение плоскости, проходящей через точку 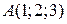 и ось ОХ.
и ось ОХ.
5.6. Найти уравнение плоскости, проходящей через точку 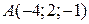 и ось ОУ.
и ось ОУ.
5.7. Найти уравнение плоскости, проходящей через точку 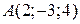 и ось ОZ.
и ось ОZ.
5.8. Найти уравнение плоскости, проходящей через точку 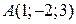 и перпендикулярной плоскостям
и перпендикулярной плоскостям 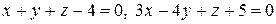
5.9. Найти уравнение плоскости, проходящей через точку 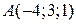 и параллельной векторам
и параллельной векторам 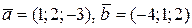 .
.
5.10. Найти уравнение плоскости, проходящей через начало координат и точки 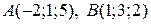 .
.
ЗАДАНИЕ № 6
ЗАДАНИЕ: Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
6.1. 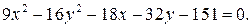
6.2. 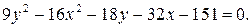
6.3. 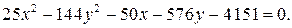
6.4. 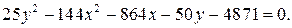
6.5. 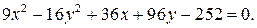
ЗАДАНИЕ: Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
6.6. 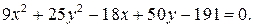
6.7. 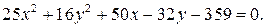
6.8. 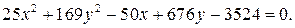
6.9. 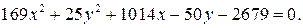
6.10. 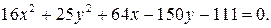
ЗАДАНИЕ № 7
ЗАДАНИЕ:Найти интеграл.
7.1. 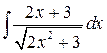 . 7.2.
. 7.2. 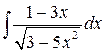 . 7.3.
. 7.3. 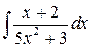 .
.
7.4. 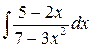 . 7.5.
. 7.5. 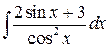 . 7.6.
. 7.6. 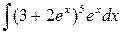 .
.
7.7. 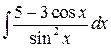 . 7.8.
. 7.8. 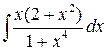 . 7.9.
. 7.9. 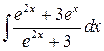 .
.
7.10. 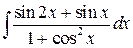 .
.
ЗАДАНИЕ № 8
ЗАДАНИЕ:Найти интеграл.
8.1. 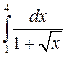 . 8.2.
. 8.2. 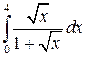 . 8.3.
. 8.3. 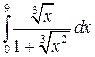 8.4.
8.4. 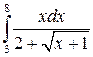
8.5.. 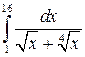 . 8.6.
. 8.6. 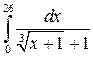 . 8.7.
. 8.7. 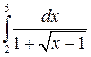 ..
..
8.8. 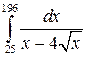 . 8.9.
. 8.9. 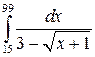 . 8.10.
. 8.10. 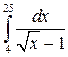 .
.
ГАПОУ СО «Областной техникум дизайна и сервиса».
– Екатеринбург, 2015. – 25 с.
