Исчисление высказываний ИВ.
Исчисление высказываний ИВ – это аксиоматическая логическая система гильбертовского типа, адекватная алгебре высказываний. Опишем это исчисление.
В качестве алфавита исчисления высказываний возьмем следующее множество символов:
1) счетное множество высказывательных переменных, обозначаемых прописными латинскими буквами с индексами и без них;
2) символы логических операций 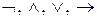 ;
;
3) скобки ( , ).
Вместе с символами алфавита будем использовать и метасимволы: латинские буквы жирного шрифта для обозначения формул и знак = для обозначения формул метасимволами.
Множество формул обычно задается индуктивным определением. Допустимыми последовательностями символов или словами в языке исчисления высказываний являются формулы алгебры высказываний. Пункты 1 и 2 этого определения определяют элементарные формулы, а п. 3 – механизм образования новых формул.
Следует заметить, что в исчислении высказываний не разрешается опускать скобки для операций с большим приоритетом, что допустимо в алгебре высказываний. Так, например, формула алгебры высказываний 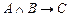 не является формулой исчисления высказываний, ее следует записать, как
не является формулой исчисления высказываний, ее следует записать, как 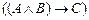 , в дальнейшем изложении мы будем опускать лишь внешние скобки.
, в дальнейшем изложении мы будем опускать лишь внешние скобки.
Следующим шагом в описании исчисления высказываний будет выделение класса формул, которые будем называть истинными или доказуемыми в исчислении высказываний. Это определение имеет такой же рекуррентный характер, как и определение формулы.
Сначала определим исходные истинные формулы, называемые аксиомами. В качестве системы аксиом примем следующие формулы (аксиоматика П.С.Новикова).
1. 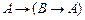
2. 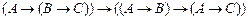
3. 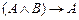
4. 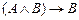
5. 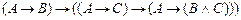
6. 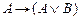
7. 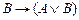
8. 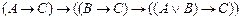
9. 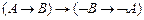
10. 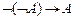
После этого определим правила, позволяющие из истинных формул образовывать новые. Эти правила, мы будем называть правилами вывода. Образование истинной формулы из исходных истинных формул или аксиом путем применения правил вывода будем называть выводом данной формулы из аксиом.
Определим правила вывода, которые являются отношениями на множестве формул.
1. Правило подстановки.
Пусть U– формула, содержащая высказывательную переменную X. Тогда если U – истинная формула в исчислении высказываний, то, заменяя в ней переменную X всюду, куда она входит, произвольной формулой B, мы также получим истинную формулу.
U(¼, X,¼)
______________________________________
U(¼, X,¼){В//X}
2. Правило заключения (modus ponens).
Если U и U®B истинные формулы в исчислении высказываний, то B также истинная формула, т.е.
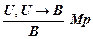
Наряду с правилом заключения, мы будем использовать и другие правила образования истинных и выводимых формул. Эти правила являются производными, при их доказательстве используется понятие выводимости в логическом исчислении, аксиомы ИВ и правило заключения.
Перечислим основные из производных правил вывода. Как и прежде, метасимволы 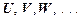 являются произвольными формулами, а через T обозначим конечное множество формул (возможно пустое). Так как доказательство большинства правил непосредственно следует из определения выводимости и аксиом ИВ, то приведём только их формулировки, доказав лишь ключевое правило 5 – в форме теоремы дедукции.
являются произвольными формулами, а через T обозначим конечное множество формул (возможно пустое). Так как доказательство большинства правил непосредственно следует из определения выводимости и аксиом ИВ, то приведём только их формулировки, доказав лишь ключевое правило 5 – в форме теоремы дедукции.
1. Правило повторения посылки.
T, 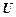 |-
|- 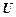
2. Правило введения посылки.
ЕслиT |- 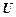 , тоT,
, тоT, 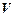 |-
|- 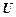 .
.
3. Правило удаления посылки.
Если T, 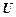 |-
|- 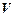 и T |-
и T |- 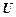 , то T |-
, то T |- 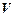 .
.
4. Правило силлогизма.
ЕслиT |- 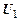 , . . . ,T |-
, . . . ,T |- 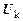 и
и 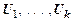 |-
|- 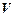 , тоT |-
, тоT |- 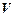 .
.
5. Правило введения импликации.
ЕслиT, 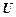 |-
|- 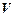 , тоT |-
, тоT |- 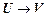 .
.
Это весьма важное свойство называют еще теоремой дедукции. Учитывая, что 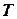 - конечное множество формул, правило 5 можно сформулировать в следующем виде:
- конечное множество формул, правило 5 можно сформулировать в следующем виде:
Теорема дедукции. Если
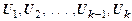 |- B,
|- B,
то
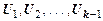 |-
|- 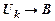 .
.
6. Правило удаления импликации.
ЕслиT |- 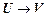 , тоT,
, тоT, 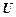 |-
|- 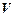 .
.
7. Правило введения конъюнкции.
T, 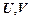 |-
|- 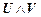 .
.
8. Правило удаления конъюнкции.
T, 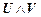 |-
|- 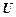 ,
,
T, 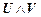 |-
|- 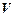 .
.
9. Правило введения дизъюнкции.
T, 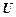 |-
|- 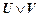 ,
,
T, 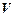 |-.
|-. 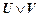
10. Правило удаления дизъюнкции.
Если T, 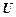 |-
|- 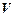 и T,
и T, 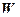 |-
|- 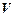 , то T,
, то T, 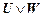 |-
|- 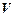 .
.
11. Правило введения отрицания.
Если T, 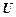 |-
|- 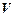 и T,
и T, 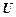 |-
|- 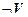 , то T |-
, то T |- 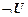 .
.
12. Правило удаления отрицания.
T, 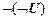 |-
|- 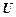
13. Правило контрапозиции. 
Если T, 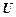 |-
|- 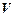 , то T,
, то T, 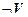 |-
|- 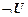 .
.
Правила 1-13 называют обычно правилами естественного вывода, а вывод формулы из системы посылок, при котором используются эти правила, - естественным выводом.
Рассмотрим примеры вывода формул с использованием правил естественного вывода. Всюду далее, строя вывод формулы, будем рядом с каждой формулой последовательности указывать применяемое правило (его номер), а затем, в круглых скобках, номера формул исходных посылок, к которым применялось данное правило.
Задание 1. Доказать, что в ИВ
|- 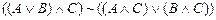 .
.
Решение. Для доказательства эквивалентности формул в ИВ достаточно построить два вывода:
1) 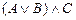 |-
|- 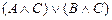 ;
;
2) 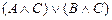 |-
|- 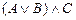 .
.
Построим 1-й вывод.
1. 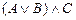 |- |- 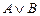 | |
2. 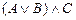 |- C |- C | |
3. 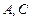 |- |- 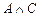 | |
4. 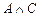 |- |- 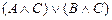 | |
5. 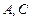 |- |- 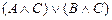 | 4 (3, 4) |
6. 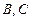 |- |- 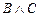 | |
7. 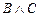 |- |- 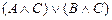 | |
8. 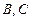 |- |- 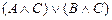 | 4 (6, 7) |
9. 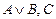 |- |- 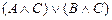 | 10 (5, 8) |
10. 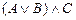 |- |- 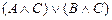 | 4 (1, 2, 9) |
Обратный вывод имеет вид
1. 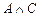 |-A |-A | |
2. A |- 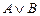 | |
3. 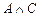 |- |- 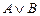 | 4 (1, 2) |
4. 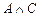 |-C |-C | |
5. 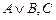 |- |- 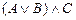 | |
6. 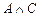 |- |- 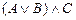 | 4 (3, 4, 5) |
7. 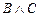 |-B |-B | |
8. B |- 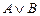 | |
9. 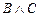 |- |- 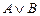 | 4 (7, 8) |
10. 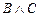 |-C |-C | |
11. 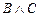 |- |- 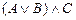 | 4 (9, 10, 5) |
12. 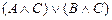 |- |- 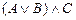 | 10 (6, 11) |
Задание 2. Доказать, что
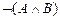 |-
|- 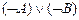
Решение.
1. 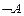 |- |- 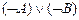 | |
2. 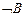 |- |- 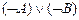 | |
3. 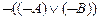 |- |- 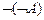 | 13 (1) |
4. 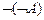 |- A |- A | |
5. 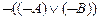 |- A |- A | 4 (3, 4) |
6. 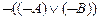 |- |- 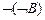 | 13 (2) |
7. 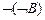 |- B |- B | |
8. 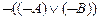 |- B |- B | 4 (6, 7) |
9. 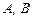 |- |- 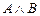 | |
10. 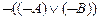 |- |- 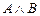 | 4 (5, 8, 9) |
11. 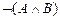 |- |- 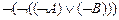 | 13 (10) |
12. 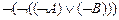 |- |- 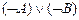 | |
13. 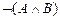 |- |- 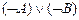 | 4 (11, 12) |
Задание 3. Доказать, что
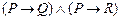 |-
|- 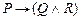
Решение.
1. 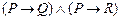 |- |- 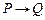 | |
2. 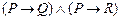 |- |- 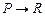 | |
3. 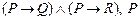 |- Q |- Q | 6 (1) |
4. 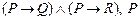 |- R |- R | 6 (2) |
5. 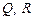 |- |- 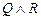 | |
6. 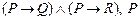 |- |- 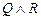 | 4 (3, 4, 5) |
7. 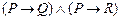 |- |- 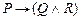 | 5 (6) |
Задание 4. Доказать, что
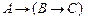 |-
|- 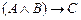
Решение.
1. 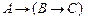 |- |- 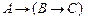 | |
2. 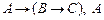 |- |- 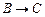 | 6 (1) |
3. 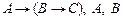 |- С |- С | 6 (2) |
4. 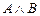 |- A |- A | |
5. 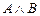 |- B |- B | |
6. 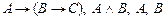 |- С |- С | 2 (3) |
7. 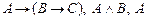 |- С |- С | 3 (6, 5) |
8. 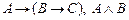 |- С |- С | 3 (7, 4) |
9. 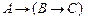 |- |- 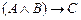 | 5 (8) |
Задание 5. Доказать, что
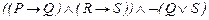 |-
|- 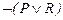
Решение. Построим вывод этой формулы.
1. 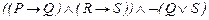 |- |- 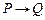 | |
2. 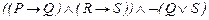 |- |- 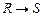 | |
3. 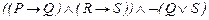 |- |- 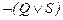 | |
4. 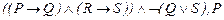 |- |- 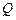 | 6 (1) |
5. 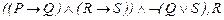 |- |- 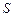 | 6 (2) |
6. 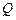 |- |- 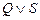 | |
7. 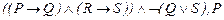 |- |- 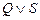 | 4 (4, 6) |
8. 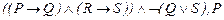 |- |- 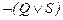 | 2 (3) |
9. 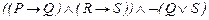 |- |- 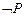 | 11 (7, 8) |
10. 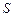 |- |- 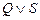 | |
11. 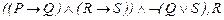 |- |- 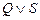 | 4 (5, 10) |
12. 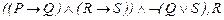 |- |- 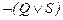 | 2 (3) |
13. 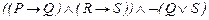 |- |- 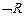 | 11 (11, 12) |
14. 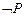 , , 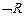 |- |- 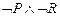 | |
15. 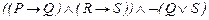 |- |- 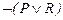 | 4 (9, 13, 14) |
16. 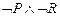 |- |- 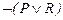 | Теорема ИВ |
17. 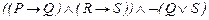 |- |- 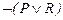 | 4 (15, 16) |
Варианты заданий
Применяя правила подстановки и заключения, доказать, что следующие формулы являются теоремами исчисления высказываний (1 – 8).
1. 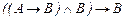
2. 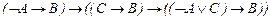
3. 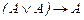
4. 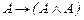
5. 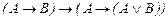
6. 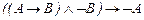
7. 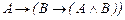
8. 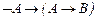
Применяя правила подстановки и заключения, построить вывод формул из данной системы посылок (9 - 13).
9. 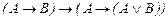
10. 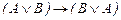
11. 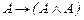
12. 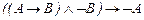
13. 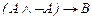
Являются ли выводами в исчислении высказываний следующие последовательности формул (14 – 16).
14. 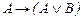
15. 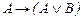
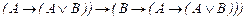
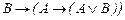
16. 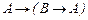
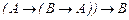
B
Применяя производные правила вывода, показать, что доказуемы формулы (17 – 34).
17. U ® B, P ® Q ú- (U Ù P) ® (B Ù Q)
18. U ® B, P ® Q ú- (U Ú P) ® (B Ú Q)
19. U ® B, P ® Q ú- (B ® P) ® (U ® Q)
20. 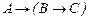 ú-
ú- 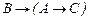
21. 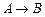 ú-
ú- 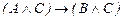
22. (P ® Q) ® ((Q ® R) ® (P ® R))
23. (P ® Q) ® ((R ® P) ® (R ® Q))
24. Q ® R ® (P Ú Q) ®(P Ú R)
25. (P ® Q) Ú (Q ® P),
26. P ® (Q® (P Ù Q))
27. (P ® Q) Ú (P ® ØQ)
28. (P ® Q)®((P ® (Q ® R)) ® (P ® R)))
29. (P ® Q)®((P ® (Q ® R)) ® (P ® R)))
30. ((P® Q) ® ((P ® Ø Q) ® Ø P))
31. (( Ø Q ® Ø P) ® ((Ø Q ® P) ® Q))
32. Q ® ((P Ú Q) Ù (Q Ú Ø P)
33. Q Ú (P Ù Ø Q) ® (P Ú Q)
34. Q ® (P Ú Ø R Ù Q Ú Q)
Применяя производные правила вывода, построить вывод формул (35 – 41).
35. 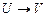 ,
, 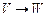 ú-
ú- 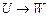
36. 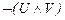 ú-
ú- 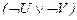
37. 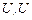 ú-
ú- 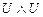
38. 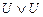 ú-
ú- 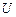
39. 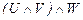 ú-
ú- 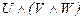
40. 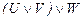 ú-
ú- 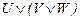
41. 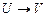 ú-
ú- 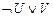
Применяя производные правила вывода, построить вывод формул. Проверить, справедлива ли выводимость в обратную сторону, если да, то построить вывод (42 – 57).
42. 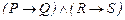 ú-
ú- 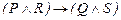
43. 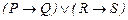 ú-
ú- 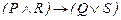
44. 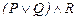 ú-
ú- 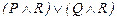
45. 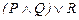 ú-
ú- 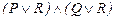
46. 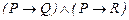 ú-
ú- 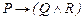
47. 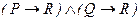 ú-
ú- 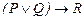
48. 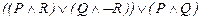 ú-
ú- 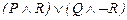
49. 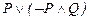 ú-
ú- 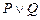
50. A ® (C ® P) ú- (A Ù C) ® P
51. 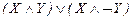 ú-
ú- 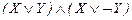
52. 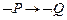 ú- (
ú- ( 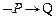 )® P
)® P
53. P® Q ú- (P® 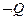 )®
)® 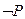
54. P Ú R Ú Q ú- ((P ® R) ® (( 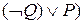 ® R)
® R)
55. (P ® Q) ® (P ® (Q ® R)) ú- ( P® R)
56. 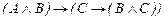 ú-
ú- 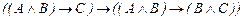
57. 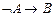 ú-
ú- 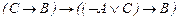
Исчисления предикатов.
Определим исчисление предикатов гильбертовского типа ИП. Это исчисление является расширением исчисления высказываний ИВ.
В алфавит ИВ добавим строчные латинские буквы для обозначения предметных переменных и символы кванторов " и $. Язык исчисления составляют формулы, определяемые также, как в алгебре предикатов.
Аксиоматика исчисления дополняется двумя схемами аксиом:
11. 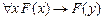
12. 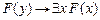 ,
,
где 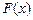 - произвольная формула, содержащая свободные вхождения переменной x, причем ни одно из них не находится в области действия квантора по переменной y, а
- произвольная формула, содержащая свободные вхождения переменной x, причем ни одно из них не находится в области действия квантора по переменной y, а 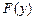 получена из
получена из 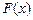 заменой свободных вхождений x на y.
заменой свободных вхождений x на y.
К правилу заключения ИВ добавляются два правила, связанные с кванторами. Пусть 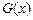 и
и 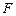 – формулы, которые содержат и не содержат свободные вхождения переменной x соответственно.
– формулы, которые содержат и не содержат свободные вхождения переменной x соответственно.
2. Правило обобщения (введения ")
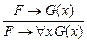 .
.
3. Правило введения $
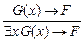 .
.
Правила естественного вывода дополняются 4-мя правилами. Пусть
14. Правило введения квантора ".
Если T |- U(x), то T |- "xU(x).
15. Правило удаления квантора ".
Если T |- "xU(x), то T |- U(y).
16. Правило введения квантора $.
Если T |- U(y), то T |- $xU(x).
17. Правило удаления квантора $.
Если T, U(x) |- V, то T, $xU(x) |- V.
Рассмотрим примеры вывода в ИП.
Задание 1. Доказать, что в ИП
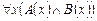 |-
|- 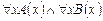 .
.
Решение.
1. 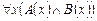 |- |- 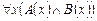 | |
2. 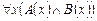 |- |- 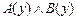 | 15 (1) |
3. 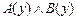 |- |- 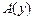 | |
4. 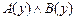 |- |- 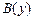 | |
5. 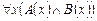 |- |- 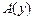 | 4 (2, 3) |
6. 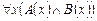 |- |- 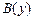 | 4 (2, 4) |
7. 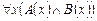 |- |- 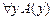 | 14 (5) |
8. 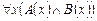 |- |- 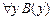 | 14 (6) |
9. 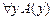 |- |- 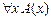 | Теорема ИП |
10. 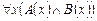 |- |- 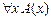 | 4 (7, 9) |
11. 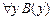 |- |- 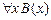 | Теорема ИП |
12. 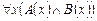 |- |- 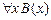 | 4 (8, 11) |
13. 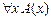 , , 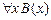 |- |- 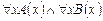 | |
14. 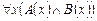 |- |- 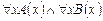 | 4 (10, 12, 13) |
Задание 2. Доказать, что в ИП
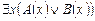 |-
|- 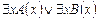 .
.
Решение.
1. 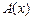 |- |- 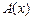 | |
2. 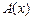 |- |- 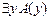 | 16 (1) |
3. 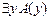 |- |- 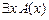 | Теорема ИП |
4. 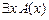 |- |- 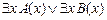 | |
5. 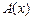 |- |- 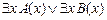 | 4 (2, 3, 4) |
6. 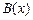 |- |- 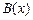 | |
7. 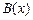 |- |- 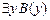 | 16 (6) |
8. 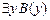 |- |- 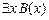 | Теорема ИП |
9. 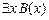 |- |- 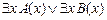 | |
10. 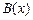 |- |- 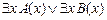 | 4 (7, 8, 9) |
11. 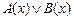 |- |- 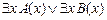 | 10 (5, 10) |
12. 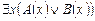 |- |- 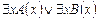 | 17 (11) |
Прикладные исчисления предикатов строятся добавлением к исчислению предикатов своих собственных аксиом. Причем, в прикладных исчислениях предикатов вводится понятие терма. Термами являются:
1) предметные переменные и константы;
2) предметные функции.
В аксиомах прикладных исчислений предикатов наряду с предметными переменными могут использоваться произвольные термы.
Всюду далее будут рассматриваться прикладные исчисления предикатов первого порядка, т. е. исчисления, в которых кванторами связываются только предметные переменные, а не предикаты и функции.
Исчисление с равенством.
В данном исчислении вводится предикат =, а к аксиомам ИП добавляются аксиомы равенства.
E1. 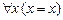
E2. 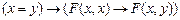
Здесь Е1 является аксиомой, а Е2 – схемой аксиомы, где 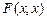 – произвольная формула, а
– произвольная формула, а 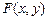 – формула, полученная из
– формула, полученная из 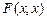 заменой некоторых вхождений x на y.
заменой некоторых вхождений x на y.
Теорема.В любой теории с равенством:
1) |- 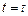 для любого терма t;
для любого терма t;
2) |- 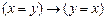 ;
;
3) |- 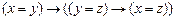 .
.
Формальная арифметика.
Формальная арифметика определяется как исчисление с равенством на предметном множестве ô, в котором вводятся предметная константа 0 и предметные функции + , × , ¢ , задаваемые аксиомами.
A1. 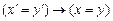
A2. 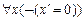
A3. 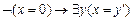
A4. 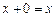
A5. 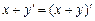
A6. 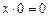
A7. 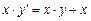
A8. 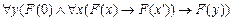
Здесь А1-А7 – аксиомы, а А8 – схема аксиомы, определяющая доказательство по индукции.
Задание 3. Доказать, что в формальной арифметике
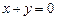 |-
|- 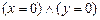 .
.
Решение.Рассмотрим вначале идею доказательства, а затем оформим её в виде формального вывода. Доказательство проведём от противного, предположим, что 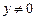 , тогда у него существует предыдущий элемент t, такой что
, тогда у него существует предыдущий элемент t, такой что 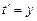 . Так как
. Так как 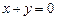 , то
, то 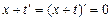 , что противоречит аксиоме А2, следовательно,
, что противоречит аксиоме А2, следовательно, 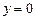 . Тогда по условию
. Тогда по условию 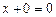 , а в силу А4
, а в силу А4 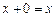 , а, значит,
, а, значит, 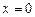 .
.
1. 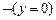 |- |- 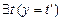 | 6 (А3) |
2. 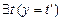 , , 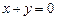 |- |- 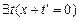 | 6 (Е2) |
3. 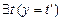 , , 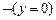 , , 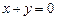 |- |- 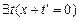 | 2 (2) |
4. 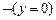 , , 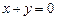 |- |- 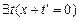 | 3 (1, 3) |
5. 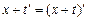 | А5 |
6. 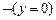 , , 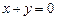 |- |- 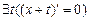 | Свойство 3) предиката = |
7. |- 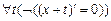 | А2 |
8. 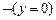 , , 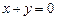 |- |- 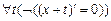 | 2 (7) |
9. 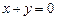 |- |- 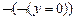 | 11 (6, 8) |
10. 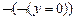 |- |- 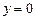 | |
11. 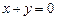 |- |- 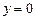 | 4 (9, 10) |
12. 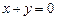 , , 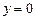 |- |- 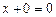 | 6 (Е2) |
13. 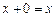 | А4 |
14. 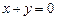 , , 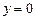 |- |- 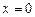 | Свойство 3) предиката |
15. 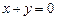 |- |- 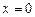 | 3 (11, 14) |
16. 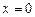 , , 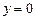 |- |- 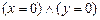 | |
17. 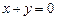 |- |- 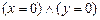 | 4 (11, 15, 16) |
Задание 4. Распространить формальную арифметику на множество целых чисел Ù.
Решение. Для того чтобы распространить формальную арифметику на множество Ù, нужно определить константу 0 и предметные функции на множестве Ù, используя определённые на множестве ô функции и константу.
Так как оба множества ô и Ù счётны, то между ними можно установить взаимнооднозначное соответствие, т. е 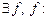 ô ®Ù . Тогда определим 0 множества Ù как образ нулевого элемента ô 0Ù =
ô ®Ù . Тогда определим 0 множества Ù как образ нулевого элемента ô 0Ù = 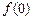 . Для того чтобы определить функцию следования для целого элемента z, возьмём прообраз этого элемента из ô, вычислим для него следующий элемент, а затем отобразим его в Ù, т. е.
. Для того чтобы определить функцию следования для целого элемента z, возьмём прообраз этого элемента из ô, вычислим для него следующий элемент, а затем отобразим его в Ù, т. е. 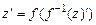 . Аналогично определяются функции + и × :
. Аналогично определяются функции + и × :
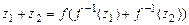 ,
,
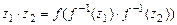 .
.
