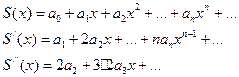Степенные ряды. Теорема Абеля. Область сходимости степенного ряда и ее основные характеристики: центр сходимости и радиус сходимости степенного ряда
Рассмотрим ряд, членами которого являются степенные функции от аргумента x:
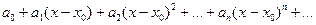
Такой ряд называется степенным. В этом ряде действительные числа 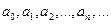 называются коэффициентами степенного ряда, величина x0 –произвольно заданное действительное число, одно и то же для всех членов ряда, x - аргумент нашего функционального ряда. Величины
называются коэффициентами степенного ряда, величина x0 –произвольно заданное действительное число, одно и то же для всех членов ряда, x - аргумент нашего функционального ряда. Величины 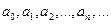 и x0 полностью задают степенной ряд. ьКраткая запись ряда:
и x0 полностью задают степенной ряд. ьКраткая запись ряда: 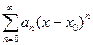 . В случае x0 = 0 имеем ряд
. В случае x0 = 0 имеем ряд 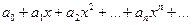 . Заметим, что при помощи преобразования x-x0 = y можно свести задачу изучения ряда
. Заметим, что при помощи преобразования x-x0 = y можно свести задачу изучения ряда 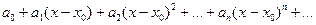 к изучению более простого ряда
к изучению более простого ряда 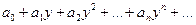 (в дальнейшем вместо y пишем x).
(в дальнейшем вместо y пишем x).
Для степенного ряда 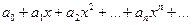 имеет место теорема Абеля:
имеет место теорема Абеля:
Если степенной ряд 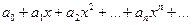 сходится в некоторой точке x0, отличной от нуля (x0 ¹ 0), то он сходится, причем абсолютно, и в любой точке x, удовлетворяющей условию
сходится в некоторой точке x0, отличной от нуля (x0 ¹ 0), то он сходится, причем абсолютно, и в любой точке x, удовлетворяющей условию 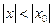 . Докажем это.
. Докажем это.
Так как ряд 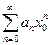 сходится, то его общий член
сходится, то его общий член 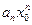 стремится к нулю при стремлении номера n к бесконечности. Следовательно, члены этого ряда ограничены как члены сходящейся (к нулю) последовательности
стремится к нулю при стремлении номера n к бесконечности. Следовательно, члены этого ряда ограничены как члены сходящейся (к нулю) последовательности 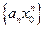 . Это означает, что существует такое положительное число M >0, что для всех номеров n выполняются неравенства:
. Это означает, что существует такое положительное число M >0, что для всех номеров n выполняются неравенства: 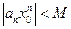 . Тогда берем произвольное x (
. Тогда берем произвольное x ( 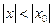 )ирассмотрим ряд:
)ирассмотрим ряд: 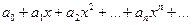 = =
= = 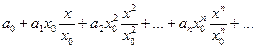 . Оценим абсолютную сходимость этого ряда :
. Оценим абсолютную сходимость этого ряда : 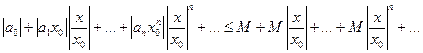 - сходится, ибо это геометрическая прогрессия со знаменателем
- сходится, ибо это геометрическая прогрессия со знаменателем 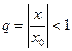 .
.
Следствие. Если ряд 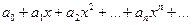 расходится при x0, то он расходится и при любом x,
расходится при x0, то он расходится и при любом x, 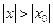 .
.
Область сходимости степенного ряда .
Из теоремы Абеля и следствия из нее вытекает, что если степенной ряд 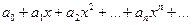 имеет отличные от нуля точки сходимости x0 и точки расходимости x1, то всякая точка сходимости лежит к началу координат не дальше, чем точка расходимости. При этом получается, что точки сходимости степенного ряда заполняют некоторый промежуток на числовой оси x с центром в начале координат. Этот промежуток можно характеризовать числом R таким, что в точках x,
имеет отличные от нуля точки сходимости x0 и точки расходимости x1, то всякая точка сходимости лежит к началу координат не дальше, чем точка расходимости. При этом получается, что точки сходимости степенного ряда заполняют некоторый промежуток на числовой оси x с центром в начале координат. Этот промежуток можно характеризовать числом R таким, что в точках x, 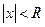 ряд сходится (причем абсолютно), а в точках x ,
ряд сходится (причем абсолютно), а в точках x , 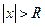 - ряд расходится. В точках x=-R и x=R ряд может как сходиться, так и расходиться. Существование R можно объяснить так:
- ряд расходится. В точках x=-R и x=R ряд может как сходиться, так и расходиться. Существование R можно объяснить так:
в точке x*, лежащей между x0 и x1, будет либо сходимость, либо расходимость; так и перебираем точки отрезка [x0,x1], пока не исчерпаем весь этот отрезок.
Определение. Число R называется радиусом сходимости степенного ряда 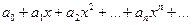 , если для всякого
, если для всякого 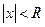 ряд сходится, а для всякого
ряд сходится, а для всякого 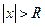 ряд расходится. Интервал (-R, R) называют интервалом сходимости, начало координат – центр интервала сходимости.
ряд расходится. Интервал (-R, R) называют интервалом сходимости, начало координат – центр интервала сходимости.
Разъяснение:
Для ряда 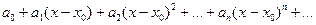 центром интервала сходимости будет точка x0 . Число R будет радиусом сходимости, если для
центром интервала сходимости будет точка x0 . Число R будет радиусом сходимости, если для 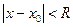 ряд сходится, а для
ряд сходится, а для 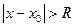 ряд расходится. Интервал сходимости этого ряда: -R+x0 < x <R+x0 . На концах интервала сходимости x=-R+x0 и x= R+x0 ряд может либо сходиться, либо расходиться.
ряд расходится. Интервал сходимости этого ряда: -R+x0 < x <R+x0 . На концах интервала сходимости x=-R+x0 и x= R+x0 ряд может либо сходиться, либо расходиться.
Для отыскания радиуса сходимости , характеризующего область сходимости степенного ряда, можно поступать с рядом, как с числовым – применять к нему признаки Даламбера, Коши и другие.
Пусть, например, существует предел 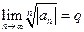 . Тогда находим
. Тогда находим 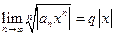 ;
; 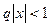 ;
; 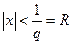 . Если q=0, то вся действительная ось x является областью сходимости. Если q= ¥, то ряд сходится только в точке x=0, а на всей оси x он расходится. Если же
. Если q=0, то вся действительная ось x является областью сходимости. Если q= ¥, то ряд сходится только в точке x=0, а на всей оси x он расходится. Если же 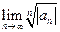 не существует (но, допустим, существует самая правая предельная точка (точка сгущения) числовой последовательности
не существует (но, допустим, существует самая правая предельная точка (точка сгущения) числовой последовательности 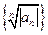 , то обозначив эту правую точку через
, то обозначив эту правую точку через 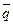 находим, что заведомо ряд будет сходиться, если
находим, что заведомо ряд будет сходиться, если 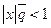 , т.е. если
, т.е. если 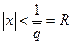
Аналогично поступаем при применении признака Даламбера. Пусть существует 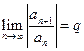 . Тогда
. Тогда
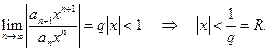 Сходимость ряда на концах x=-R и x=R исследуется отдельно.
Сходимость ряда на концах x=-R и x=R исследуется отдельно.
45. Аналитические свойства суммы степенных рядов:
1. Степенной ряд 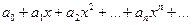 равномерно (правильно) сходится на любом замкнутом интервале [-b, b], находящемся внутри интервала сходимости (-R, R). Действительно, берем любое x0, лежащее между b и R:
равномерно (правильно) сходится на любом замкнутом интервале [-b, b], находящемся внутри интервала сходимости (-R, R). Действительно, берем любое x0, лежащее между b и R: 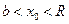 . Тогда для любого
. Тогда для любого 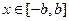 ряд
ряд 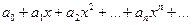 мажорируется числовым рядом
мажорируется числовым рядом 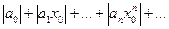 , который сходится. Следовательно, и наш степенной ряд сходится равномерно по признаку Вейерштрасса.
, который сходится. Следовательно, и наш степенной ряд сходится равномерно по признаку Вейерштрасса.
2. Степенной ряд, составленный из производных 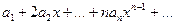 имеет тот же радиус сходимости R, что и исходный ряд
имеет тот же радиус сходимости R, что и исходный ряд 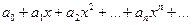 . Это свойство легко доказывается в случае существования предела
. Это свойство легко доказывается в случае существования предела 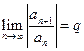 . Тогда
. Тогда 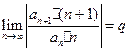 что и требовалось.
что и требовалось.
Отсюда в частности следует, что все степенные ряды, получаемые почленным дифференцированием исходного ряда, имеют один и тот же радиус сходимости. Все эти ряды будут сходиться правильно на замкнутом отрезке, лежащем внутри интервала сходимости.
3. Сумма степенного ряда непрерывна в каждой точке x0 интервала (-R, R) (ибо он сходится равномерно на отрезке [-x0, x0]). Рассмотрим пример ряда: 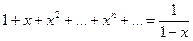 =S(x). Функция S(x) разрывна только при x=1, но вне интервала сходимости
=S(x). Функция S(x) разрывна только при x=1, но вне интервала сходимости 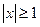 она не является суммой ряда.
она не является суммой ряда.
4. Степенные ряды можно почленно интегрировать в интервале сходимости (-R, R). Пусть a и b – точки, лежащие внутри (-R, R). Тогда будем иметь:
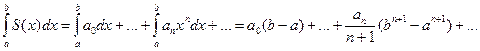
5. Степенные ряды можно почленно дифференцировать в любой точке интервала сходимости, причем будем иметь: